课题学习(七)----粘滑运动的动态算法
一、 粘滑运动的动态算法
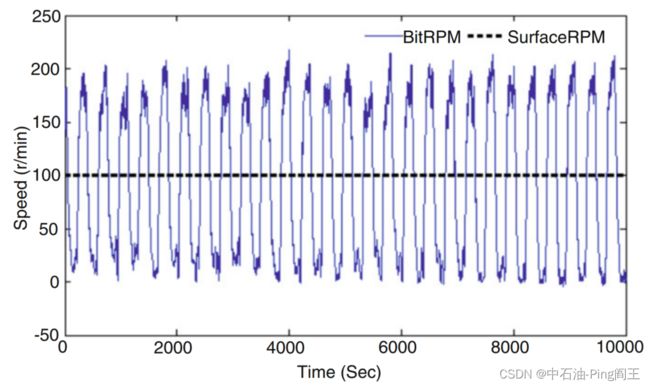
在实际钻井过程中,钻柱会出现扭振和粘滑现象(粘滑运动–B站视频连接),但并不总是呈现均匀旋转。如下图所示,提取一段地下数据时,转盘转速保持在100 r/min,钻头转速在0-200 r/min之间波动,粘滑现象非常严重。在这种情况下,基于钻柱均匀旋转的理论模型将不可行。
"粘滑运动"是一个物理学术语,通常用于描述物体在两个表面之间运动时的特性。它包括了两种主要类型的摩擦:
1.粘性摩擦(也称为动摩擦):这是指当两个物体之间相对运动时,由于它们之间的接触表面不是完全光滑的,所以会产生的摩擦力。这种摩擦力随着相对速度的增加而增加,但在某一点上会达到一个极限值,称为静摩擦系数。
2.滑动摩擦:这是指当一个物体相对于另一个物体开始运动时所产生的摩擦力。滑动摩擦力通常比静摩擦力小,一旦物体开始移动,滑动摩擦力会保持相对稳定。
这两种摩擦力可以用数学公式来描述,通常使用静摩擦系数(μs)和动摩擦系数(μk)来表示。 公式如下:
静摩擦力(Fs):Fs ≤ μs * N
其中,N是物体间的垂直压力或重力。
动摩擦力(Fk):Fk = μk * N
其中,N是物体间的垂直压力或重力。
理解粘滑运动对于设计和工程应用非常重要,因为它影响了许多日常物体和机器的性能。例如,汽车轮胎与路面之间的摩擦力决定了车辆的牵引力和制动效果。
首先分析了钻柱的运动,实际计算出在整个钻井过程中出现粘滑现象的频率。使用研制的旋转导向系统进行了多次现场试验,测量数据表明,在钻井过程中会频繁出现粘滑振动。
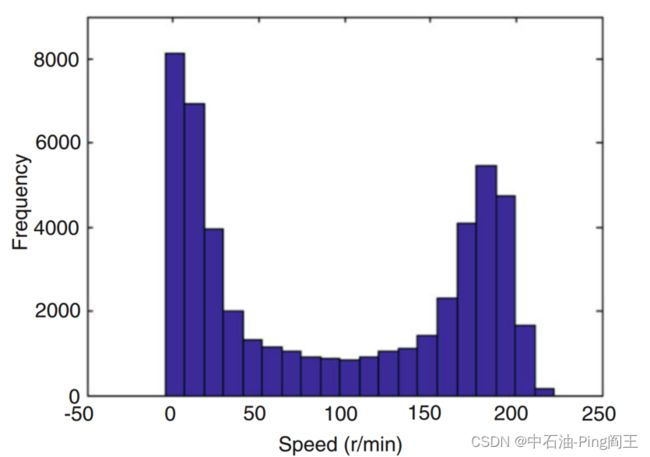
我们利用储层采样原理随机选取2 h的速度数据,根据样本的特征估计总体特征。 首先选取1 h的数据点顶部;假设有k个数据点;从第k + 1个数据点到达最后一个数据点;选择概率为1/i (i=k + 1, k + 2,…,N)的第i个数据点,并随机替换之前选择的一个元素。这个遍历时间可以保证1 h的数据点完全随机选择。如下图所示,接近于零的速度表示出现了粘滑。粘滑振动在钻井过程中始终存在,因此应用粘滑振动法提高测量精度是可行的。
1.1 实验数据
利用式(3.30)、式(3.31)和设计好的滤波器,建立DSP程序。将整个系统放到实验台上进行测量系统的精度测试。下图显示了加速度计(x、y、z轴)和磁通门(x、y、z轴)的测量数据。

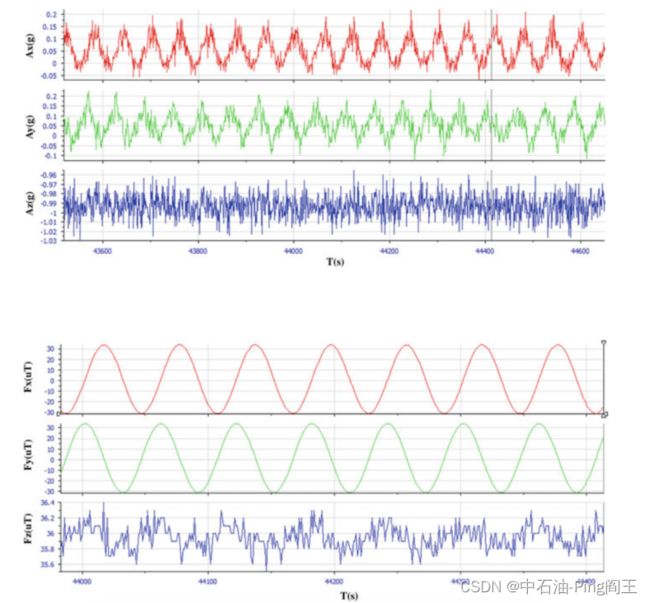
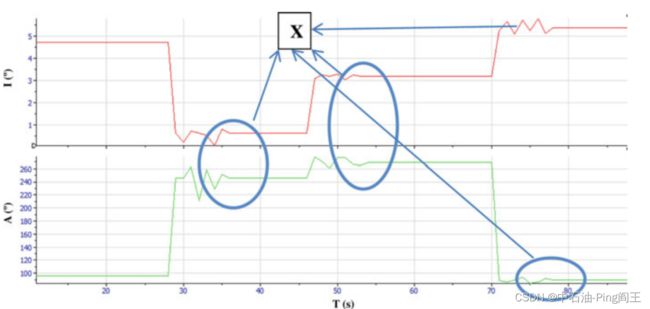
可以看出,加速度计的测量噪声相对大于磁通门;主要原因是加速度计对钻柱振动的敏感性。通过滤波可以得到一定程度上对噪声的消除。最后,试验中的倾角和方位角值如下图所示。其中X区为旋转钻柱振动噪声情况下的计算结果。
1.2 现场数据分析
在实际应用中,我们采用了低通滤波和移动平均滤波等方法,但在钻柱旋转时,效果并不理想。如下图所示,钻柱旋转时,倾角和方位角波动较大,而瞬时静止时,倾角和方位角波动明显较小,这促使我们寻求一种利用钻柱瞬时静止时数据的方法,以提高整个过程的精度。
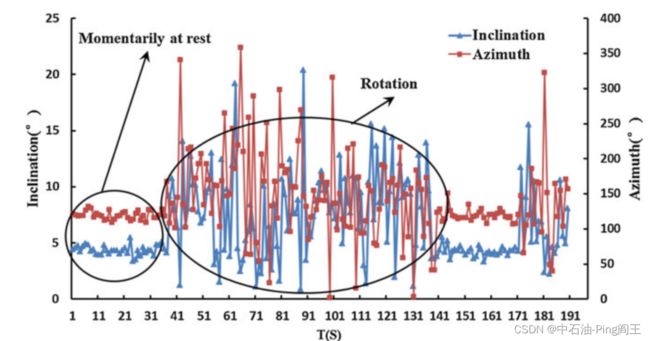
时间序列如上图所示,倾角和方位角每10 s计算一次,井下传感器采样频率为100 Hz。也就是说,每次计算使用1000个数据点,因此我们可以看到上图中的非旋转区域持续了大约400 s(论文中写的是400s,但是从图中我并没有看出持续了400s,有点像40s)。这是钻井过程中人为停止的结果。实际上,井下钻柱在地面似乎处于连续旋转状态时也会自动停止( 这就是粘滑运动带来的效果,其实说白了,就是一走一停的现象) 。
为了在更小的时间尺度上观察,如下图所示,采样频率为100 Hz, 500个数据点代表5秒。这些数据甚至不足以计算出上图中的一个点,但是我们找到了一个静止的区域,我们称之为粘性区域。在粘滞区,磁通门信号保持在固定值,加速度计信号有一定波动,但比钻柱旋转时的表现小得多。通过安装结构可以推断,y轴信号与x轴相似,相位相差90度°,所以图中没有显示y轴信号。
显然,在旋转时,加速度计信号也应该像磁通门信号一样呈现正弦波,但由于钻柱的强烈振动,我们没有看到这个结果。

z轴加速度计信号也受到相对较小的振动的影响。我们使用移动平均滤波器进行进一步处理,如下式所示: A n = ∑ i = 1 10 a i A n + i − 9 , a i = 1 10 A_n = \sum_{i=1}^{10}a_iA_{n+i-9},a_i=\frac{1}{10} An=i=1∑10aiAn+i−9,ai=101
滤波后的信号得到了很大的改善,如图下图所示。在本章中,我们还使用FIR滤波器消除信噪比。对于磁通门信号,由于不受振动的影响,噪声信号被认为是高频分量。
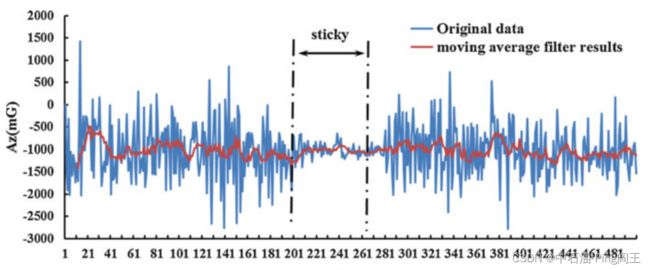
预处理后可进入动力计算部分。我们需要设置一个时间窗口来实时判断钻柱的运动状态。最大限度地利用隐藏在原始测量信号中的准确信息,提高最终的测量精度。
1.3 粘滑振动现象分析
首先要分析钻柱的运动,实际上是要 弄清楚在整个钻井过程中出现粘滑现象的频率。研制的旋转导向系统进行了多次现场试验,试验数据回放表明,粘滑振动的发生频率很高。由于数据量大,对整个测量数据进行分析既费时又费力。
因此,我们利用储层采样原理]随机选取2 h的速度数据,以便从样本的数据中估计总体特征。首先选择顶部1 h的数据点,假设有k个数据点,从第k + 1个数据点到最后一个数据点,选择第i个点的概率为 1 i \frac{1}{i} i1,并随机替换先前选择的元素。这个遍历时间得到1 h的数据点可以保证完全随机选择。
由下图可以看出,在零附近的速度表示出现了粘滑。粘滑振动在钻井过程中始终存在,因此应用粘滑振动法提高测量精度是可行的。

1.4 利用粘滑振动提高测量精度
1.4.1 粘滑振动的应用方法
下图提出了旋转钻柱底部姿态的动态求解方法,即在非旋转情况下,三轴实时信号滤波全部用于计算,同时存储x、y轴滤波信号;在旋转状态下,采用z轴实时滤波信号和非旋转管柱的x、y轴存储信号。
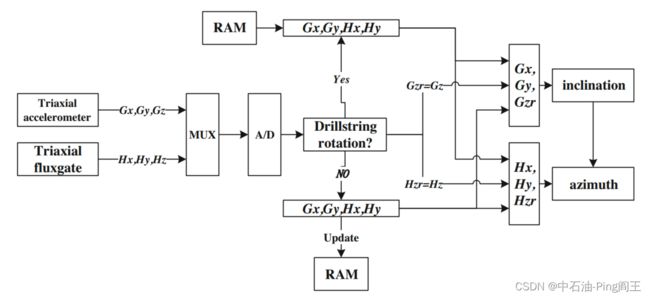
此外,井下钻具的粘滑状态被视为一种不旋转的“静止”状态。提出了基于井下实测数据的管柱旋转状态实时判断方法。钻柱转速可用于判断钻柱是否旋转,是一种切实可行的方法,但可靠性不高。通过以上分析,用标准差统计方法来确定钻柱运动将会更好,因为它反映了组内个体之间的分散程度。使用50个数据点作为时间窗口,假设为x1, x2,…, x49, x50,将得到标准差σ。如下图所示,当标准差接近于零时,钻柱力矩可以认为是静态的。
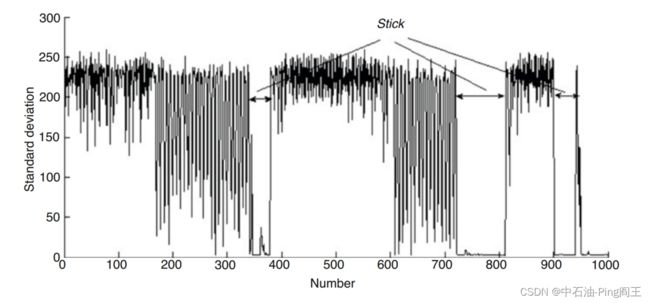
1.4.2 卡尔曼滤波
卡尔曼滤波是一种最优递归数据处理算法。它是最优的,因为它使用所有可用的信息来最小化给定系统状态变量中的错误。它是递归的,因为它不需要将所有以前的数据保存在存储中。它也是一种数据处理算法,因为它不是电滤波器,而是计算机程序。为了实现离散卡尔曼滤波器,误差模型必须以状态空间形式给出: x k = F k , k − 1 + G k − 1 w k − 1 ( 3.93 ) x_k = F_{k,k-1}+G_{k-1}w_{k-1} (3.93) xk=Fk,k−1+Gk−1wk−1(3.93) y k = H k x k + v k ( 3.94 ) y_k=H_kx_k+v_k(3.94) yk=Hkxk+vk(3.94)
式(3.93)称为动力学方程,式(3.94)为观测或更新方程。这里 x k x_k xk是过程状态向量, F k , k − 1 F_{k,k-1} Fk,k−1是 x k {x_k} xk与 x k − 1 x_{k-1} xk−1之间的方阵,称为状态转移矩阵,而 w k − 1 w_{k-1} wk−1是一个随机函数,以 G k − 1 {G_{k-1}} Gk−1为系数向量,被认为是白噪声。在式(12)中, y k {y_k} yk为第k时刻的测量向量, H k {H_k} Hk为给出观测向量与状态向量之间理想无噪声关系的设计矩阵, v k {v_k} vk为观测随机噪声。假设 v k {v_k} vk与 w k − 1 {w_{k-1}} wk−1无关。
定义刀具面为φ,倾角为θ,方位为ψ。变换矩阵Rn b可以定义为:
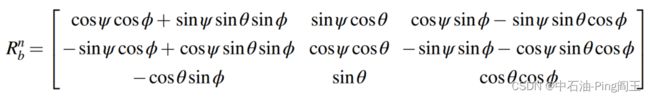
设 G b = [ G x G y G y ] T G^b=\begin{bmatrix}G_x &G_y &G_y\end{bmatrix}^T Gb=[GxGyGy]T,转速分别在xyz轴上定义为 w x , w y , w z w_x,w_y,w_z wx,wy,wz, w i b b = [ w x w y w y ] T w_{ib}^b=\begin{bmatrix}w_x &w_y &w_y\end{bmatrix}^T wibb=[wxwywy]T,则得到旋转角度。

用四元数 Q = [ q 1 q 2 q 3 q 4 ] T Q=\begin{bmatrix}q1 &q2 &q3&q4\end{bmatrix}^T Q=[q1q2q3q4]T表示坐标系变换,则 R n b R_n^b Rnb可以重新定义为:
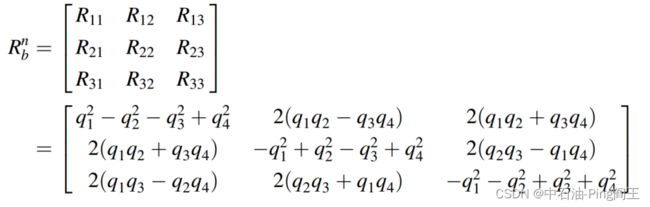
然后得到倾角和方位角求解的动力学方程:
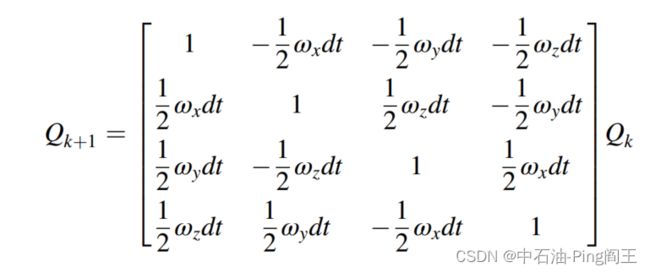
1.4.2 仿真效果
我们提取了旋转钻柱状态下的4000个数据点,Matlab仿真结果如下图所示。由此可见,利用粘滑现象,大大提高了钻柱动态旋转时的井眼倾角和方位角计算精度。
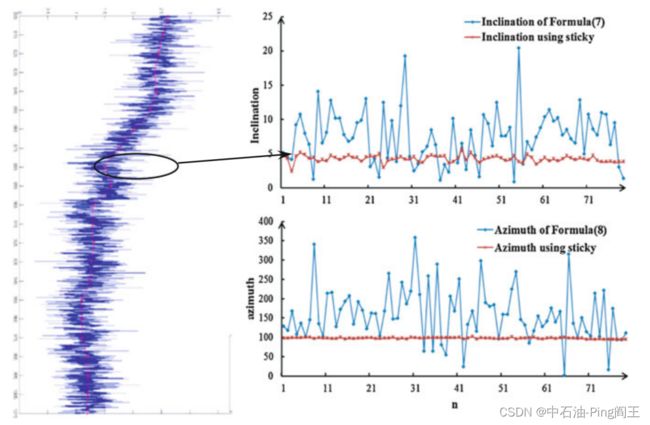
在定向钻井和旋转导向钻井技术及应用中,随着钻柱的旋转,如何实时准确测量井底钻具的空间姿态(倾角、方位、刀面)是一个具有挑战性的问题。仿真和实验表明,本章提出的动态求解方法能够满足工程要求。但钻柱的振动严重影响了动态求解的精度。通过对现场资料的统计分析,我们发现粘滑现象普遍存在,因此我们利用粘滑状态来开发一种动态算法,以提高井眼倾角和方位求解器的精度。仿真和实验评价结果表明,所设计的算法具有良好的实用性。这对定向钻井和旋转导向技术的发展具有参考意义。
二、 往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法