HAWQ:基于 Hessian 的混合精度神经网络量化
HAWQ:基于 Hessian 的混合精度神经网络量化
-
-
- 摘要
- 动机
- 方法
-
- 海森方法的有效性分析
- 海森矩阵方法推导
-
- 根据幂迭代求海森矩阵的最大特征值
- 根据海森矩阵最大特征值确定量化精度与顺序
- 实验结果
-
- ResNet20 On CIFAR-10
- ResNet50 on ImageNet
- SqueezeNext on ImageNet
- Inception-V3 on ImageNet
- 消融实验
-
- 海森混合精度量化的有效性
- Block-Wise微调的有效性
-
本文为 UC Berkeley 大学发表在 ICCV 2019上的混合精度量化论文。旨在利用Block块的 Hessian 最大特征值选择各层的相对量化精度与量化微调 Block 块的顺序,在不同网络下测试获得了不错的精度提升。
论文题目:HAWQ: Hessian AWare Quantization of Neural Networks with Mixed-Precision
论文链接:https://arxiv.org/pdf/1905.03696v1.pdf
代码链接:https://github.com/Zhen-Dong/HAWQ
摘要
在许多应用程序中部署神经网络时,模型大小和推理速度/功率已成为主要挑战。解决这些问题的一种有前途的方法是量化。但是,将模型统一量化为超低精度会导致精度显着下降。一种新颖的解决方案是使用混合精度量化,因为与其他层相比,网络的某些部分可能允许较低的精度。但是,没有系统的方法来确定不同层的精度。对于深度网络,蛮力方法不可行,因为混合精度的搜索空间在层数上是指数级的。另一个挑战是在将模型量化到目标精度时用于确定逐块微调顺序复杂度是阶乘级别的。本文介绍了 Hessian AWare 量化(HAWQ),这是一种解决这些问题的新颖的二阶量化方法。 HAWQ 根据Block块的 Hessian 最大特征值选择各层的相对量化精度。而且,HAWQ基于二阶信息为量化层提供了确定性的微调顺序。本文使用 ResNet20 在 Cifar-10 上以及用Inception-V3,ResNet50 和 SqueezeNext 模型在 ImageNet 上验证了方法的结果。将HAWQ 与最新技术进行比较表明,与 DNAS 相比,本文在 ResNet20 上使用 8 倍的激活压缩率可以达到相似/更好的精度,并且与最近提出的RVQuant和HAQ的方法相比,在ResNet50 和 Inception-V3 模型上,当缩小 14% 模型大小的情况下可以将精度提高 1%。此外,本文证明了可以将 SqueezeNext 量化为仅 1MB 的模型大小,同时在 ImageNet 上实现 Top-1 精度超过 68%。
动机
量化方法需要对NN参数(即权重)和激活都进行量化,以减少推理期间模型的总内存占用量。但是,这里的主要挑战是传统的量化方式会导致准确性的显著下降。尤其是,不可能将普通卷积网络的所有权重/激活的位数减少到超低精度,而又不显著降低精度。这是因为并非卷积网络的所有层都允许相同的量化级别。解决此问题的一种可能方法是使用混合精度量化,其中较高的精度用于网络的某些“敏感”层,而较低的精度用于“非敏感”层。但是,为每一层找到正确精度的搜索空间在层数上是指数级的。此外,为了避免准确性损失,需要对模型进行微调(即重新训练)。正如后面要讨论的,一次量化整个模型然后进行微调并不是最佳的。取而代之的是,需要执行多阶段量化,其中在网络的每个阶段将部分量化为低精度,然后进行量化感知的微调以恢复准确性。但是,用于确定首先要量化哪些层的搜索空间是层数的系数大小。为解决上述搜索空间大的问题,本文提出了一种Hessian指导的方法来应对这些挑战。本文贡献如下:
-
选择混合精度量化的搜索空间的层数是指数级的。因此,提出了一种新颖的确定性方法,用于根据每层的Hessian 频谱确定各层的相对量化级别。
-
模型的量化感知微调的搜索空间是块/层数的系数。因此,提出了一种基于 Hessian 方法来确定不同NN块的微调顺序。
-
最后进行了HAWQ的消融研究,并在 CIFAR-10 上使用 ResNet20 以及在 ImageNet 上使用 Inception-V3 / ResNet50 / SqueezeNext 提出了新颖的量化结果。与最新技术的比较表明,本文的方法实现了更高的精度(高达1%),更小的模型尺寸(高达20%)和更小的激活尺寸(高达8)。
方法
海森方法的有效性分析
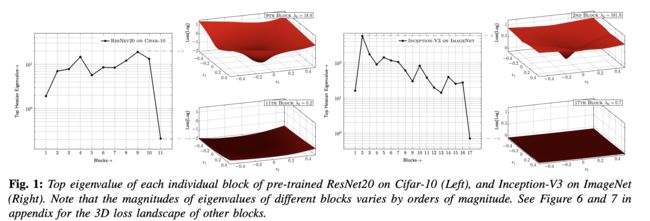
基于最小描述长度(MDL)理论,在给定的阈值下,指定一个平坦区域所需的比特数较少,反之,指定一个具有尖锐曲率的区域所需的比特数较多。更通俗的解释,平坦区域的不精确位置所产生的噪声不会被放大,使得它更容易被量化。而尖锐区域则相反,即使是小的舍去误差也会被放大。因此,预计具有较高 Hessian 频谱的层(即较大的特征值)对量化更敏感。下图显示了CIFAR-10上的ResNet20和ImageNet上的Inception-V3的这些特征值对不同块的分布。可以发现,不同的区块表现出数量级的差异。例如,ResNet20第 9 个 block 相比于最后一个 block 的扰动更为敏感。
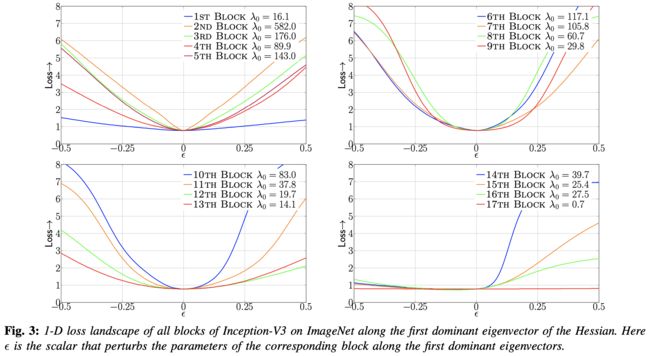
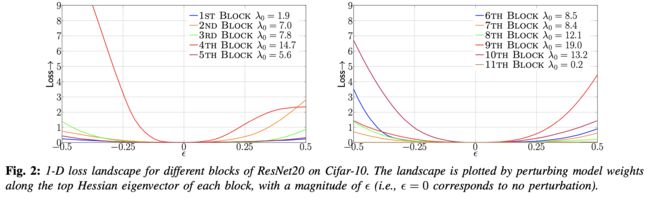
为了进一步说明这一点,本文提供了以下的一维损失可视化示意图。 首先计算出每一个 Block 的海森特征向量,然后对每一个 Block 沿着特征向量分别计算损失的变化,如下图所示分别展现了 ResNet20(在Cifar-10上)和 Inception-V3(在ImageNet上)的结果。可以清楚地看到,具有较大的 Hessian 特征值(即曲率更尖锐)的 Block 表现出较大的损失波动。
海森矩阵方法推导
假设 NN 被划分为 b 个block { B 1 , B 2 … , B b } \left\{B_{1}, B_{2} \ldots, B_{b}\right\} {B1,B2…,Bb} , 对应的权重参数表示为 { W 1 , W 2 … , W b } \left\{W_{1}, W_{2} \ldots, W_{b}\right\} {W1,W2…,Wb}。
根据幂迭代求海森矩阵的最大特征值
首先了解幂法求矩阵特征值的具体流程,如下Python代码:
# 参考代码:https://www.cnblogs.com/qizhou/p/12271287.html
import numpy as np
#矩阵A
A = np.matrix(
[[-5.6,2.,0.],
[3.,-1.,1.],
[0.,1.,3.]])
L0=2#范数类型
v = np.matrix([[-2.],[-7.],[1.]])#v0(随机值)
u = v/(np.linalg.norm(v,L0))#u0
#迭代函数
def iterate_fun(A,u,final,L):
i=0
while i<final:
v = A*u
u = v/(np.linalg.norm(v,L))
i=i+1
print("幂法特征值:")
print(np.linalg.norm(v,L))
print("numpy特征值:")
print(np.linalg.eig(A)[0])
print("幂法特征向量:")
print(u)
print("numpy特征向量:")
print(np.linalg.eig(A)[1])
iterate_fun(A,u,1000,L0)
根据下图算法1可以了解幂迭代求海森矩阵的最大特征值的具体流程,这里需要注意的是for循环的i与 W i W_{i} Wi中的i是没有关系的,另外,算法1的巧妙之处是无需求解海森矩阵就可以求出海森矩阵的特征值。根据幂迭代的算法可以求解出海森矩阵的特征值 λ i = ∥ H v ∥ 2 \lambda_{i} = \|H v\|_{2} λi=∥Hv∥2,而$ H_{i} v$ 根据下面公式推导得出恰好为 g i T v g_{i}^{T} v giTv 关于 W i W_i Wi 的偏导数。
∂ ( g i T v ) ∂ W i = ∂ g i T ∂ W i v + g i T ∂ v ∂ W i = ∂ g i T ∂ W i v = H i v \frac{\partial\left(g_{i}^{T} v\right)}{\partial W_{i}}=\frac{\partial g_{i}^{T}}{\partial W_{i}} v+g_{i}^{T} \frac{\partial v}{\partial W_{i}}=\frac{\partial g_{i}^{T}}{\partial W_{i}} v=H_{i} v ∂Wi∂(giTv)=∂Wi∂giTv+giT∂Wi∂v=∂Wi∂giTv=Hiv
根据海森矩阵最大特征值确定量化精度与顺序
-
量化精度由 S i = λ i / n i S_{i}=\lambda_{i} / n_{i} Si=λi/ni 决定。
-
量化Block的微调顺序由 $ \Omega_{i}=\lambda_{i}\left|Q\left(W_{i}\right)-W_{i}\right|_{2}^{2} $ 决定。
实验结果
ResNet20 On CIFAR-10
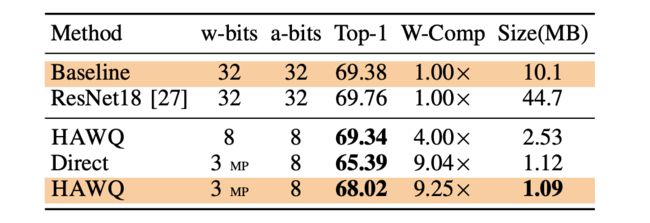
ResNet50 on ImageNet
SqueezeNext on ImageNet
Inception-V3 on ImageNet
消融实验
海森混合精度量化的有效性
Block-Wise微调的有效性
![]()