数据结构之队列

目录

队列的定义与结构

  队列的实现

队列的结构

初始化空队列

销毁队列

队尾入队列

队头出队列

获取队列头部元素

获取队列尾部元素

判断队列是否为空

获取队列长度

栈与队列经典试题

队列实现栈

栈实现队列

---

队列的定义与结构

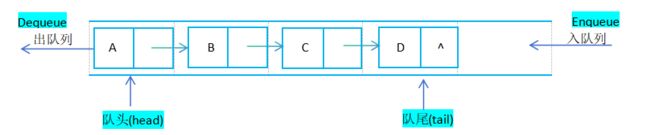
队列是一种先进先出（First In First Out）的顺序表，队列只允许在表的一端进行插入，而在另一端删除元素；队列中允许插入的一端叫做队尾，允许删除的一端称为队头；假设队列为q=(a1,a2,a3,......,an)，那么a1就是对头元素，an就是队尾元素；

入队列的顺序为a1,a2,a3,.....an，出队列的顺序为a1,a2,a3,......an退出；

  队列的实现

思考：选择数组还是链表去实现队列?

若选择数组实现队列，当元素出队列时，头部与尾部都要移动元素，时间复杂度为O(N)；

若选择链表实现队列，通过定义队头指针和队尾指针，入队列与出队列的时间复杂度为O(1);

采用单链表的思考：

队列在尾部添加元素，在头部删除元素（尾进头出)；采用链表头作为队列的头部，因为链表头部容易执行删除操作(出队)；链表尾作为队列的尾部，执行插入操作（入队)；但是执行插入操作时，首先得遍历整个链表，找到最后一个链表结点（尾结点)，才能执行插入操作（入队列），为了减少遍历，需要维护一个尾指针，指向链表尾部；使用单列表实现一个队列，链表需要维护俩个指针，头指针和尾指针；头指针指向链表头部，用于出队列；尾指针指向链表尾部，用于入队列；

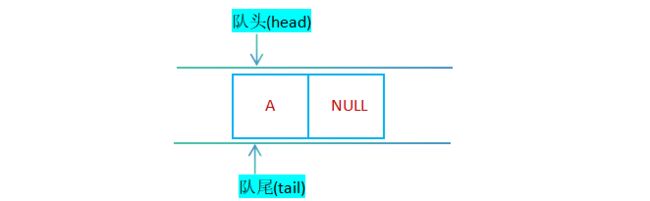
• 空队列示意图

•  空队列插入第一个元素示意图

• 入队（单链表尾插）

• 出队 （单链表头删）

队列的结构

typedef int QDataType;
typedef struct QueueNode
{
	QDataType data;//数据域
	struct QueueNode* next;//指针域-指向下一个队列结点
}QueueNode;

//当进行出队列操作(头删),需要修改队头指针，但是对于形参的修改不影响实参，只能传递二级指针；
//采取如下方案:将对头指针,队尾指针封装成结构体,只需要修改结构体指针即可修改结构体变量;
typedef struct Queue
{
	QueueNode* head;//队头指针
	QueueNode* tail;//队尾指针
	int size;//获取队列的长度
}Queue;

初始化空队列

当队头指针head与队尾指针均为空指针，且队列的长度为0，此时链队列为空；

void InitQueue(Queue* ps)
{
	assert(ps != NULL);

	ps->tail = ps->head = NULL;
	ps->size = 0;
}

销毁队列

void DestroyQueue(Queue* ps)
{
	assert(ps != NULL);
	QueueNode* cur = ps->head;
	while (cur != NULL)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur= next;
	}
	ps->head = NULL;
	ps->tail = NULL;
	ps->size = 0;
}

队尾入队列

//队尾入队列(尾插)
void QueuePush(Queue* ps, QDataType x)
{
	assert(ps != NULL);
	//创建新队列结点
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc failed:");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//入队列(尾插)
	//空队列时通过赋值完成尾插，队列中存在队列结点,按照逻辑关系完成连接;
	if (ps->tail == NULL)
	{
		ps->head = ps->tail = newnode;
	}
	else
	{
		ps->tail->next = newnode;
		ps->tail = newnode;
	}
	ps->size++;
}

队头出队列

//队头出队列(头删)
void QueuePop(Queue* ps)
{
	assert(ps != NULL);

	//空队列不可删
	assert(ps->tail != NULL);

	//出队列
	//队列中只有一个队列结点
	if (ps->head->next == NULL)
	{
		free(ps->head);
		ps->head = ps->tail = NULL;
	}
	//队列中有两个以上队列结点
	else
	{
		QueueNode* next = ps->head->next;
		free(ps->head);
		ps->head = next;
	}
	ps->size--;
}

获取队列头部元素

//获取队列头部元素
QDataType QueueFront(Queue* ps)
{
	assert(ps != NULL);
	//队列不为空
	assert(ps->head != NULL);

	return ps->head->data;
}

获取队列尾部元素

//获取队列尾部元素
QDataType QueueBack(Queue* ps)
{
	assert(ps != NULL);
	//队列不为空
	assert(ps->tail != NULL);

	return ps->tail->data;
}

判断队列是否为空

队列为空返回true，队列不为空false；

//判断队列是否为空
bool QueueEmpty(Queue* ps)
{
	assert(ps);
	if (ps->tail == NULL)
	{
		return true;
	}
	return false;
}

获取队列长度

//获取队列长度
int QueueLength(Queue* ps)
{
	assert(ps);

	return ps->size;
}

栈与队列经典试题

• 队列实现栈

题目描述：

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）；

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false

题目链接:力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

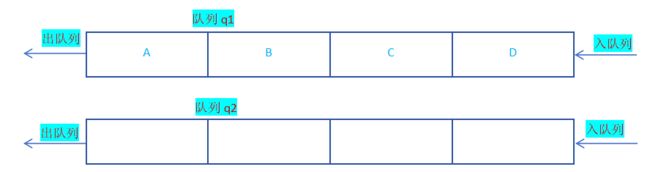
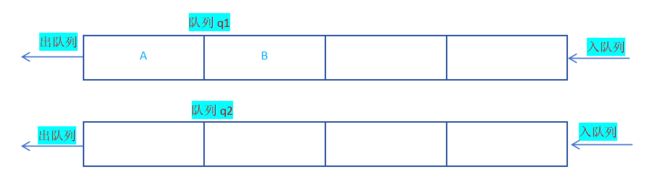
假设栈中入栈顺序为A B C D；则出栈顺序为D C B A； 如何用队列达到这种效果?

首先将栈中的数据全部存放于一个队列，其次将存放数据的队列取对头元素入空队列，直至原先存放数据的队列只剩一个数据为止；

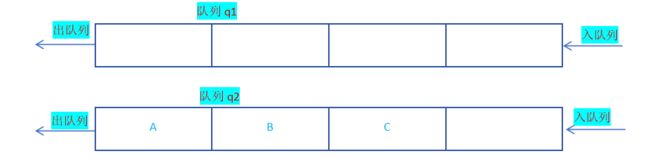
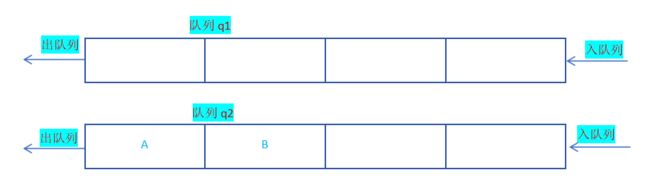
此时原先的队列只剩一个元素，调用QueuePop()函数就可达到StackPop()函数的效果，但仅仅是一个元素达到了后进先出，将元素D删除后，回到原先假设情形；

 继续将非空队列中的数据放入空队列，直至非空队列只剩1个元素，调用QueuePop()函数删除仅剩元素；

按此循环，直至两个队列全部为空；这样达到了出栈顺序为D C B A；

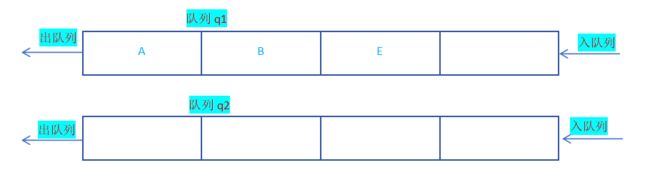
假设栈中入栈顺序为A B C D，出栈两个元素即先删除D，后删除C；然后再入栈元素E， 那么元素E应该送入那个队列？才能完成出栈顺序为D C E B A？

为了维持原先逻辑的一致性，选择将元素E送入到非空队列；然后继续按照原先逻辑pop数据；

 

 思路总结：

数据入队列时，首先判断出那个队列不是空队列，然后将数据送入非空队列；

数据出队列时，非空队列的前size-1个数据全部插入到空队列，然后删除非空队列仅剩的一个元素；两个队列始终保持一个为空；

（注：队列定义时size为队列中有效数据的个数）

typedef struct 
{
  Queue q1;
  Queue q2;
} MyStack;

MyStack* myStackCreate() 
{
   MyStack* p=(MyStack*)malloc(sizeof(MyStack));

   InitQueue(&(p->q1));
   InitQueue(&(p->q2));
   return p;
}

//那个队列不为空，数据尾插到那个队列
void myStackPush(MyStack* obj, int x) 
{
if(!QueueEmpty(&(obj->q1)))
{
   QueuePush(&(obj->q1),x);
}
//队列q1为空，无论队列q2为不为空，数据尾插到q2;
else
{
    QueuePush(&(obj->q2),x);
}
}

int myStackPop(MyStack* obj) 
{
   //首先判断那个是空队列，假设法;
   Queue* Empty=&(obj->q1);
   Queue* NonEmpty=&(obj->q2);
   if(!QueueEmpty(&(obj->q1)))
   {
       Empty=&(obj->q2);
       NonEmpty=&(obj->q1);
   }
  //空队列为Empty，非空队列为NonEmpty;
  //由于队列中包含队列的长度,需要将非空队列的前size-1个数据插入到空队列;
  //队列每出一个数据,长度自动减一，当非空队列大于1个元素，不断将非空队列的数据插入到空队列；
  while(QueueLength(NonEmpty)>1)
  {
      QueuePush(Empty,QueueFront(NonEmpty));
      QueuePop(NonEmpty);
  }
  //非空队列只剩一个元素
  int top=QueueBack(NonEmpty);
  QueuePop(NonEmpty);
  return top;
}

int myStackTop(MyStack* obj) 
{
    //由于队列始终保持一个为空,取非空队列的对头元素即为栈顶元素
   if(!QueueEmpty(&(obj->q1)))
   {
       return QueueBack(&(obj->q1));
   }
   else
   {
       return QueueBack(&(obj->q2));
   }
}

bool myStackEmpty(MyStack* obj) 
{
    //栈为空当且仅当两个队列皆为空
   return QueueEmpty(&(obj->q1))&&QueueEmpty(&(obj->q2));
}

void myStackFree(MyStack* obj) 
{
   DestroyQueue(&(obj->q1));
   DestroyQueue(&(obj->q2));

   free(obj);
}

• 栈实现队列

题目描述：

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

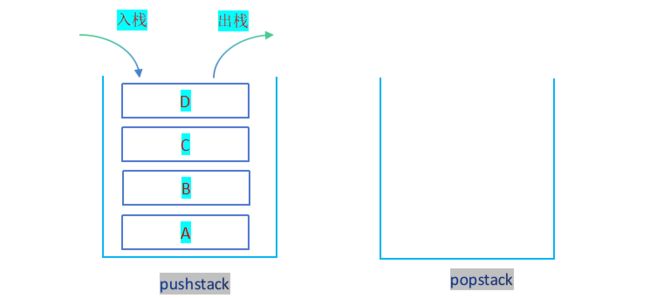
假设队列中入队列顺序为A B C D；则出队列顺序为A B C D； 如何用栈达到这种效果?

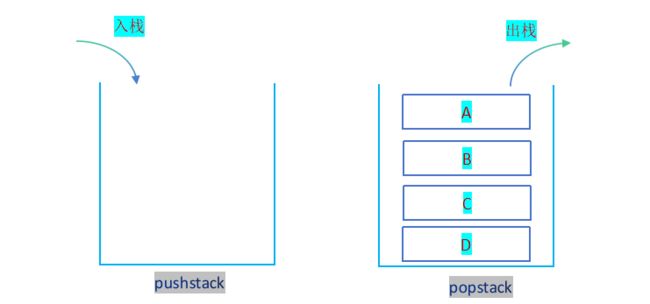
首先将队列中的数据全部存放于一个栈（pushstack），其次将存放数据的栈取栈顶元素依次入空栈(popstack)，直至原先存放数据的栈为空；

此时popstack栈不断pop(删除）数据，直至popstack栈为空；达到了入队列顺序为A B C D ，出队列顺序为A B C D ；

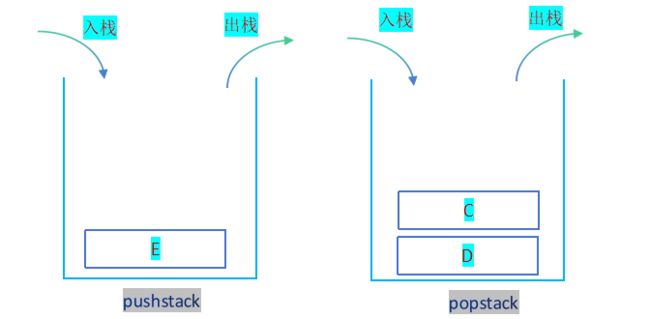
 假设队列中入队列顺序为A B C D，出队列两个元素即先删除A，后删除B；然后再入队列元素E， 那么元素E应该送入那个栈？才能完成出队列顺序为A B C D E？

数据E只能存放于空栈pushstack，只有当非空栈数据pop(删除)结束,然后将pushstack中的数据E插入到popstack栈，才能完成出队列顺序为A B C D E;

 思路总结：

数据先送入到pushstack,不断入栈，当需要出数据时，为达到先入先出的效果，将pushstack栈中的数据全部送入popstack栈中，如果此时还有数据需要入栈,全部送入pushstack中,然后不断从popstack栈中pop(删除)数据,当popstack栈为空时,再将pushstack栈中的数据全部送入popstack栈中,按此循环;

typedef struct 
{
    Stack pushstack;//入数据
    Stack popstack;//出数据
} MyQueue;

//初始化队列
MyQueue* myQueueCreate() 
{
    MyQueue* pst=(MyQueue*)malloc(sizeof(MyQueue));
    InitStack(&(pst->popstack));
    InitStack(&(pst->pushstack));
    return pst;
}

//数据入栈时全部存放于pushstack;
void myQueuePush(MyQueue* obj, int x) 
{
    StackPush(&(obj->pushstack),x);
}

//首先判断popstack栈是否为空，若popstack栈为空
//需要将pushstack栈中的数据全部送入popstack栈中;
//若popstack栈不为空,直接出数据,直到popstack为空;
int myQueuePop(MyQueue* obj) 
{
  if(StackEmpty(&(obj->popstack)))
  {
    //捯数据,将pushstack栈中的数据全部放入popstack栈中;
   while(!StackEmpty(&(obj->pushstack)))
   {
       StackPush(&(obj->popstack),StackTop(&(obj->pushstack)));
       StackPop(&(obj->pushstack));//干掉pushstack栈中栈顶元素
   }
  }
  //popstack栈不为空
   int top=StackTop(&(obj->popstack));
   StackPop(&(obj->popstack));
   return top;
}

//获取队头数据即popstack栈中即将出栈的第一个数据;
int myQueuePeek(MyQueue* obj)
{
  if(StackEmpty(&(obj->popstack)))
  {
    //捯数据,将pushstack栈中的数据全部放入popstack栈中;
   while(!StackEmpty(&(obj->pushstack)))
   {
       StackPush(&(obj->popstack),StackTop(&(obj->pushstack)));
       StackPop(&(obj->pushstack));//干掉pushstack栈中栈顶元素
   }
  }
  //popstack栈不为空
   return StackTop(&(obj->popstack));
}

//若队列为空当且仅当popstack与pushstack都为空;
bool myQueueEmpty(MyQueue* obj) 
{
   return StackEmpty(&(obj->pushstack))&&StackEmpty(&(obj->popstack));
}
//销毁队列
void myQueueFree(MyQueue* obj) 
{
    DestroyStack(&(obj->pushstack));
    DestroyStack(&(obj->popstack));
    free(obj);
}