LeetCode力扣刷题——指针三剑客之二:树
树
一、数据结构介绍
作为(单)链表的升级版,我们通常接触的树都是二叉树(binary tree),即每个节点最多有 两个子节点;且除非题目说明,默认树中不存在循环结构。LeetCode 默认的树表示方法如下。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};可以看出,其与链表的主要差别就是多了一个子节点的指针。
二、经典问题
1. 树的递归
对于一些简单的递归题,某些 LeetCode 达人喜欢写 one-line code,即用一行代码解决问题, 把 if-else 判断语句压缩成问号冒号的形式。我们也会展示一些这样的代码,但是对于新手,笔者仍然建议您使用 if-else 判断语句。
在很多时候,树递归的写法与深度优先搜索的递归写法相同,因此本书不会区分二者。
104. 二叉树的最大深度
104. Maximum Depth of Binary Tree
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
return root? 1 + max(maxDepth(root->left), maxDepth(root->right)): 0;
}
};110. 平衡二叉树
110. Balanced Binary Tree
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
解法类似于求树的最大深度,但有两个不同的地方:一是我们需要先处理子树的深度再进行 比较,二是如果我们在处理子树时发现其已经不平衡了,则可以返回一个-1,使得所有其长辈节 点可以避免多余的判断(本题的判断比较简单,做差后取绝对值即可;但如果此处是一个开销较 大的比较过程,则避免重复判断可以节省大量的计算时间)。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
return helper(root) != -1;
}
int helper(TreeNode* root){
if(!root){
return 0;
}
int left = helper(root->left), right = helper(root->right);
if(left == -1 || right == -1 || abs(left - right) > 1){
return -1;
}
return 1 + max(left, right);
}
};543. 二叉树的直径
543. Diameter of Binary Tree
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
注意:两结点之间的路径长度是以它们之间边的数目表示。
同样的,我们可以利用递归来处理树。解题时要注意,在我们处理某个子树时,我们更新的 最长直径值和递归返回的值是不同的。这是因为待更新的最长直径值是经过该子树根节点的最长直径(即两侧长度);而函数返回值是以该子树根节点为端点的最长直径值(即一侧长度),使用这样的返回值才可以通过递归更新父节点的最长直径值)。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 主函数
int diameterOfBinaryTree(TreeNode* root) {
int diameter = 0;
depth(root, diameter);
return diameter;
}
// 辅函数 - 深度递归
int depth(TreeNode* node, int& diameter){
if(!node) return 0;
int l = depth(node->left, diameter), r = depth(node->right, diameter);
diameter = max(l + r, diameter); // 更新直径长度
return 1 + max(l, r); // 返回深度
}
};437. 路径总和 III
437. Path Sum III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
递归每个节点时,需要分情况考虑:(1)如果选取该节点加入路径,则之后必须继续加入连 续节点,或停止加入节点(2)如果不选取该节点加入路径,则对其左右节点进行重新进行考虑。 因此一个方便的方法是我们创建一个辅函数,专门用来计算连续加入节点的路径。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 主函数
int pathSum(TreeNode* root, int targetSum) {
if(!root) return 0;
return pathSumStartWithRoot(root, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum);
}
// 辅函数 - 对当前节点连续加入节点,判断是否满足
long long pathSumStartWithRoot(TreeNode* root, long long targetSum){
if(!root) return 0;
long long count = root->val == targetSum? 1: 0;
count += pathSumStartWithRoot(root->left, targetSum - root->val);
count += pathSumStartWithRoot(root->right, targetSum - root->val);
return count;
}
};101. 对称二叉树
101. Symmetric Tree
给你一个二叉树的根节点 root , 检查它是否轴对称。
判断一个树是否对称等价于判断左右子树是否对称。笔者一般习惯将判断两个子树是否相等 或对称类型的题的解法叫做“四步法”:(1)如果两个子树都为空指针,则它们相等或对称(2) 如果两个子树只有一个为空指针,则它们不相等或不对称(3)如果两个子树根节点的值不相等, 则它们不相等或不对称(4)根据相等或对称要求,进行递归处理。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return helper(root->left, root->right);
}
bool helper(TreeNode* left, TreeNode* right){
if(!left && !right) return true;
if(!left || !right) return false;
if(left->val != right->val) return false;
return helper(left->left, right->right) && helper(left->right, right->left);
}
};1110. 删点成林
1110. Delete Nodes And Return Forest
给出二叉树的根节点 root,树上每个节点都有一个不同的值。
如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
这道题最主要需要注意的细节是如果通过递归处理原树,以及需要在什么时候断开指针。同 时,为了便于寻找待删除节点,可以建立一个哈希表方便查找。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector delNodes(TreeNode* root, vector& to_delete) {
vectorforest;
unordered_set dict(to_delete.begin(), to_delete.end());
root = helper(root, dict, forest);
// 自下而上最顶点的节点是处理不到,所以递归完后需要对最顶点的节点做处理
if(root){
forest.push_back(root);
}
return forest;
}
TreeNode* helper(TreeNode* root, unordered_set &dict, vector &forest){
if(!root) return root;
// 先进行递归操作,目的是自下而上对树进行操作,即树的后序遍历
root->left = helper(root->left, dict, forest);
root->right = helper(root->right, dict, forest);
// 如果存在一个节点的val值存在于to_delete数组中
if(dict.count(root->val)){
// 把当前的左右子树压入forest数组中
if(root->left){
forest.push_back(root->left);
}
if(root->right){
forest.push_back(root->right);
}
root = nullptr; // 删除当前节点
}
return root;
}
}; 2. 层次遍历
我们可以使用广度优先搜索进行层次遍历。注意,不需要使用两个队列来分别存储当前层的 节点和下一层的节点,因为在开始遍历一层的节点时,当前队列中的节点数就是当前层的节点 数,只要控制遍历这么多节点数,就能保证这次遍历的都是当前层的节点。
637. 二叉树的层平均值
637. Average of Levels in Binary Tree
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10^-5 以内的答案可以被接受。
利用广度优先搜索,我们可以很方便地求取每层的平均值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector averageOfLevels(TreeNode* root) {
vector ans;
if(!root) return ans;
queue q;
q.push(root);
while(!q.empty()){
int count = q.size();
double sum = 0;
for(int i=0; ival;
if(node->left){
q.push(node->left);
}
if(node->right){
q.push(node->right);
}
}
ans.push_back(sum / count);
}
return ans;
}
}; 2. 前中后序遍历
前序遍历、中序遍历和后序遍历是三种利用深度优先搜索遍历二叉树的方式。它们是在对节 点访问的顺序有一点不同,其它完全相同。考虑如下一棵树:
前序遍历先遍历父结点,再遍历左结点,最后遍历右节点,我们得到的遍历顺序是 [1 2 4 5 3 6]。
void preorder(TreeNode *root){
visit(root);
preorder(root->left);
preorder(root->right);
}中序遍历先遍历左节点,再遍历父结点,最后遍历右节点,我们得到的遍历顺序是 [4 2 5 1 3 6]。
void inorder(TreeNode *root){
inorder(root->left);
visit(root);
inorder(root->right);
}后序遍历先遍历左节点,再遍历右结点,最后遍历父节点,我们得到的遍历顺序是 [4 5 2 6 3 1]。
void postorder(TreeNode *root){
postorder(root->left);
postorder(root->right);
visit(root);
}105. 从前序与中序遍历序列构造二叉树
105. Construct Binary Tree from Preorder and Inorder Traversal
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
对于任意一颗树而言,前序遍历的形式总是:
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是:
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
我们通过本题的样例讲解一下本题的思路。前序遍历的第一个节点是 4,意味着 4 是根节点。 我们在中序遍历结果里找到 4 这个节点,根据中序遍历的性质可以得出,4 在中序遍历数组位置 的左子数组为左子树,节点数为 1,对应的是前序排列数组里 4 之后的 1 个数字(9);4 在中序 遍历数组位置的右子数组为右子树,节点数为 3,对应的是前序排列数组里最后的 3 个数字。有了这些信息,我们就可以对左子树和右子树进行递归复原了。为了方便查找数字的位置,我们可以用哈希表预处理中序遍历的结果。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
unordered_map index;
public:
TreeNode* buildTree(vector& preorder, vector& inorder) {
int n = preorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for(int i=0; i& preorder, const vector& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right){
if(preorder_left > preorder_right){
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = buildTreeHelper(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = buildTreeHelper(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
}; 144. 二叉树的前序遍历
144. Binary Tree Preorder Traversal
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
因为递归的本质是栈调用,因此我们可以通过栈来实现前序遍历。注意入栈的顺序。
递归写法:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector ans;
helper(root, ans);
return ans;
}
void helper(TreeNode* root, vector& ans){
if(!root){
return;
}
ans.push_back(root->val);
helper(root->left, ans);
helper(root->right, ans);
}
};
栈写法:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector ans;
if(!root) return ans;
stack s;
s.push(root);
while(!s.empty()){
TreeNode* node = s.top();
s.pop();
ans.push_back(node->val);
if(node->right){
s.push(node->right);
}
if(node->left){
s.push(node->left);
}
}
return ans;
}
}; 3. 二叉查找树
二叉查找树(Binary Search Tree, BST)是一种特殊的二叉树:对于每个父节点,其左子树中 所有节点的值小于等于父结点的值,其右子树中所有节点的值大于等于父结点的值。因此对于一 个二叉查找树,我们可以在 O(log n) 的时间内查找一个值是否存在:从根节点开始,若当前节点 的值大于查找值则向左下走,若当前节点的值小于查找值则向右下走。同时因为二叉查找树是有 序的,对其中序遍历的结果即为排好序的数组。
一个二叉查找树的实现如下。
template
class BST{
struct Node{
T data;
Node* left;
Node* right;
}
Node* root;
Node* makeEmpty(Node* t){
if(t == NULL) return NULL;
makeEmpty(t->left);
makeEmpty(t->right);
delete t;
return NULL;
}
Node* insert(Node* t, T x){
if(t == NULL){
t = new Node;
t->data = x;
t->left = t->right = NULL;
}else if(x < t->data){
t->left = insert(t->left, x);
}else if(x > t->data){
t->right = insert(t->right, x);
}
return t;
}
Node* find(Node* t, T x){
if(t == NULL) return NULL;
if(x < t->data) return find(t->left, x);
if(x > t->data) return find(t->right, x);
return t;
}
Node* findMin(Node* t){
if(t == NULL || t->left == NULL) return t;
return findMin(t->left);
}
Node* findMax(Node* t){
if(t == NULL || t->right == NULL) return t;
return findMax(t->right);
}
Node* remove(Node* t ,T x){
Node* temp;
if(t == NULL){
return NULL;
}else if(x < t->data){
t->left = remove(t->left, x);
}else if(x > t->data){
t->right = return(t->right, x);
}else if(t->left && t->right){
temp = findMin(t->right);
t->data = temp->data;
t->right = remove(t->right, t->data);
}else{
temp = t;
if(t->left == NULL){
t = t->right;
}else if(t->right == NULL){
t = t->left;
}
delete temp;
}
return t;
}
public:
BST(): root(NULL){}
~BST(){
root = makeEmpty(root);
}
void insert(T x){
insert(root, x);
}
void remove(T x){
remove(root, x);
}
};
99. 恢复二叉搜索树
99. Recover Binary Search Tree
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
我们可以使用中序遍历这个二叉查找树,同时设置一个 prev 指针,记录当前节点中序遍历 时的前节点。如果当前节点小于 prev 节点的值,说明需要调整次序。
有一个技巧是如果遍历整个序列过程中只出现了一次次序错误,说明就是这两个相邻节点需要被交换;如果出现了两次次序错误,那就需要交换这两个节点。
class Solution {
public:
void recoverTree(TreeNode* root) {
TreeNode *mistake1 = nullptr, *mistake2 = nullptr, *prev = nullptr;
inorder(root, mistake1, mistake2, prev);
if(mistake1 && mistake2){
int temp = mistake1->val;
mistake1->val = mistake2->val;
mistake2->val = temp;
}
}
void inorder(TreeNode* root, TreeNode* &mistake1, TreeNode* &mistake2, TreeNode* &prev){
if(!root) return;
if(root->left){
inorder(root->left, mistake1, mistake2, prev);
}
if(prev && root->val < prev->val){
if(!mistake1){
mistake1 = prev;
mistake2 = root;
}else{
mistake2 = root;
}
}
prev = root;
if(root->right){
inorder(root->right, mistake1, mistake2, prev);
}
}
};669. 修剪二叉搜索树
669. Trim a Binary Search Tree
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
利用二叉查找树的大小关系,我们可以很容易地利用递归进行树的处理。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root){
return root;
}
if(root->val > high){
return trimBST(root->left, low, high);
}
if(root->val < low){
return trimBST(root->right, low, high);
}
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};4. 字典树
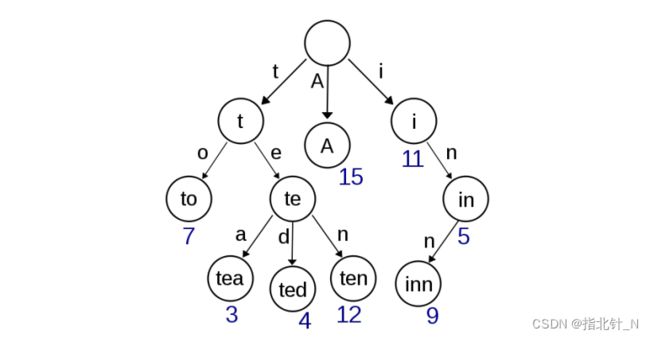
字典树/前缀树(Trie)用于判断字符串是否存在或者是否具有某种字符串前缀。
为什么需要用字典树解决这类问题呢?假如我们有一个储存了近万个单词的字典,即使我们 使用哈希,在其中搜索一个单词的实际开销也是非常大的,且无法轻易支持搜索单词前缀。然而 由于一个英文单词的长度 n 通常在 10 以内,如果我们使用字典树,则可以在 O(n)——近似 O(1) 的时间内完成搜索,且额外开销非常小。
208. 实现 Trie (前缀树)
208. Implement Trie (Prefix Tree)
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
以下是字典树的典型实现方法。
class TrieNode{
public:
TrieNode* childNode[26];
bool isVal;
TrieNode(): isVal(false) {
for(int i=0; i<26; ++i){
childNode[i] = nullptr;
}
}
};
class Trie {
TrieNode* root;
public:
Trie(): root(new TrieNode()) {
}
// 向字典树插入一个词
void insert(string word) {
TrieNode* temp = root;
for(int i=0; ichildNode[word[i] - 'a']){
temp->childNode[word[i] - 'a'] = new TrieNode();
}
temp = temp->childNode[word[i] - 'a'];
}
temp->isVal = true;
}
// 判断字典树里是否有一个词
bool search(string word) {
TrieNode* temp = root;
for(int i=0; ichildNode[word[i] - 'a'];
}
return temp? temp->isVal: false;
}
// 判断字典树是否有一个以词开始的前缀
bool startsWith(string prefix) {
TrieNode* temp = root;
for(int i=0; ichildNode[prefix[i] - 'a'];
}
return temp;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/ 三、巩固练习
欢迎大家共同学习和纠正指教