数据结构与算法——顺序表的实现及原理
目录
一、顺序表的原理
1.什么是顺序表?
2.什么是线性表
3.顺序表与链表的区别
二、顺序表的实现
1.顺序表的初始化
顺序表的定义:
顺序表的初始化
2.顺序表数据在尾部插入
3.顺序表数据在头部插入
4.顺序表数据在尾部的删除
5.顺序表数据在头部的删除
6.顺序表数据在任意位置插入
7.顺序表数据在任意位置删除
8.顺序表元素的查找
9.顺序表元素的修改
10.顺序表元素的打印
11.顺序表的销毁
总结
一、顺序表的原理
1.什么是顺序表?
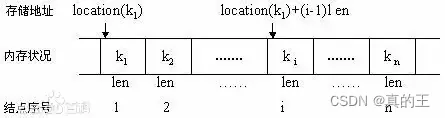
顺序表是在计算机内存中以数组的形式保存的线性表,线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的各个元素、使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中,即通过数据元素物理存储的相邻关系来反映数据元素之间逻辑上的相邻关系,采用顺序存储结构的线性表通常称为顺序表。顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。
2.什么是线性表
线性表是最基本、最简单、也是最常用的一种数据结构。线性表(linear list)是数据结构的一种,一个线性表是n个具有相同特性的数据元素的有限序列。
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的(注意,这句话只适用大部分线性表,而不是全部。比如,循环链表逻辑层次上也是一种线性表(存储层次上属于链式存储,但是把最后一个数据元素的尾指针指向了首位结点)。
3.顺序表与链表的区别
顺序表的本质是数组,它能够动态增长,但是它里面储存的数据必须是从左往右是连续的,
它的逻辑结构与物理结构是一致的
这是物理结构,而它的逻辑结构是一个数组,也是连续的。
顺序表的缺陷:1.动态增容有性能消耗还伴随着一定的空间浪费
2.头部插入数据需要挪动数据
所以在现实生活中,我们很少使用顺序表储存数据
链表:链表的空间是按需所取,头部插入数据时不需要挪动数据,它的物理结构与逻辑结构是不一致的,因为链表的节点是我们动态开辟出来的 ,我们只知道这个节点会指向下一个节点,但是我们并不清楚它的下一个节点在内存中存储的真实位置
4.线性表与数组的区别
通过上面的线性表的定义,我们清楚的知道线性表是包含数组的
二、顺序表的实现
1.顺序表的初始化
我们要知道顺序表是用来存储数据的,所以顺序表的节点一定可以存储数据,我们可以通过下标来访问顺序表的任意位置,同时我们还要知道顺序表节点的编号,来更好的访问,还要有顺序表的容量方便我们进行扩容,那么知道了这些我们就可以很清楚的写出顺序表的初始化
顺序表的定义:
typedef int SeqDataType;
typedef struct SeqList
{
SeqDataType* array;
SeqDataType sz;
SeqDataType capacity;
}SeqList;顺序表的初始化
//初始化顺序表
void SeqListInit(SeqList* pq)
{
pq->array = (SeqDataType*)malloc(sizeof(SeqDataType) * 3);
if (pq->array == NULL)
{
perror("SeqListInit::malloc");
exit(-1);
}
pq->capacity = 3;
pq->sz = 0;
}
2.顺序表数据在尾部插入
我们在思考如何在顺序表的尾部插入数据时我们会想到一个问题?
如果顺序表满了该怎么办呢?
我们可以进行扩容,但是扩大多少呢?
扩大的容量过大会导致空间的浪费,扩大的太小会导致频繁申请内存,拖慢程序运行速度
综合考虑,扩大到原容量的二倍算是比较好的。
//检查容量
void SeqCheckCapacity(SeqList* pq)
{
assert(pq);
if (pq->capacity == pq->sz)
{
SeqDataType* p = (SeqDataType*)realloc(pq->array, sizeof(SeqDataType) * pq->capacity * 2);
if (p == NULL)
{
perror("SeqCheckCapacity::realloc");
exit(-1);
}
pq->array = p;
}
}这里解决了容量问题,那么接下来我们就开始在尾部插入数据
//在尾部插入数据
void SeqListPushBack(SeqList* pq, SeqDataType x)
{
assert(pq);
SeqCheckCapacity(pq);
pq->array[pq->sz] = x;
pq->sz++;
}3.顺序表数据在头部插入
在头部插入数据与在尾部插入数据类似,但是我们要想在头部插入,必须将数组中的元素全体向后移动,之后在开始插入数据
//头插
void SeqListPushFront(SeqList* pq, SeqDataType x)
{
assert(pq);
SeqCheckCapacity(pq);
//将数据全体向后移动一位
int end = pq->sz - 1;
while (end >= 0)
{
pq->array[end+ 1] = pq->array[end];
end--;
}
pq->array[0] = x;
pq->sz++;
}4.顺序表数据在尾部的删除
尾部删除比较简单,我们只要吧sz向前挪动一位就可以解决这个问题
void SeqListPopBack(SeqList* pq)
{
assert(pq);
pq->sz--;
}5.顺序表数据在头部的删除
头部删除与头插的思路差不多,都是要将数组中的元素整体移动,来实现目的
//头删
void SeqListPopFront(SeqList* pq)
{
assert(pq);
assert(pq->sz > 0);
int begin = 0;
while (begin < pq->sz)
{
pq->array[begin] = pq->array[begin + 1];
begin++;
}
pq->sz--;
}6.顺序表数据在任意位置插入
//在任何位置插入
void SeqListInsert(SeqList* pq, int pos, SeqDataType x)
{
assert(pq);
assert(pos >= 0 && pos <= pq->sz);
SeqCheckCapacity(pq);
int end = pq->sz - 1;
while (end >= pos)
{
pq->array[end + 1] = pq->array[end];
end--;
}
pq->array[pos] = x;
pq->sz++;
}7.顺序表数据在任意位置删除
//在任何位置删除
void SeqListErase(SeqList* pq, int pos)
{
assert(pq);
assert(pos >= 0 && pos <= pq->sz);
int begin = 0;
while (beginsz)
{
pq->array[begin] = pq->array[begin + 1];
begin++;
}
pq->sz--;
} 8.顺序表元素的查找
//查找
int SeqListFind(SeqList* pq,SeqDataType x)
{
assert(pq);
for (int i = 0; i < pq->sz; i++)
{
if (pq->array[i] == x)
{
printf("找到了\n");
return i;
}
}
return -1;
}9.顺序表元素的修改
//修改顺序表
void SeqListModify(SeqList* pq,int pos, SeqDataType x)
{
assert(pq);
assert(pos >= 0 && pos <= pq->sz);
pq->array[pos] = x;
}10.顺序表元素的打印
//打印
void SeqListPrint(SeqList* pq)
{
assert(pq);
for (int i = 0; i < pq->sz; i++)
{
printf("%d ", pq->array[i]);
}
}11.顺序表的销毁
因为我们的数组是动态开辟出来的所以我们需要手动释放空间,来避免出现内存泄漏
//销毁
void SeqListDestory(SeqList* pq)
{
assert(pq);
free(pq->array);
pq->array = NULL;
}总结
以上就是顺序表的相关内容。