【数据结构】常见排序算法详细分析(内含java与c++代码)
目录
- 前言
- 1. 定义
- 2. 插入排序
-
- 2.1 直接插入排序
- 2.2 折半插入排序
- 2.3 希尔排序
- 3. 交换排序
-
- 3.1 冒泡排序
- 3.2 快速排序
- 4. 选择排序
-
- 4.1 简单选择排序
- 4.2 堆排序
- 5. 归并排序
- 6. 总结
前言
排序是计算机程序设计中的一种重要操作, 在很多领域中都有广泛的应用
在考研复试和企业面试都会有很强的考察需求
1. 定义
排序(Sorting) :是按关键字的非递减或非递增顺序对一组记录重新进行排列的操作
关于排序的稳定性标准
定义如下:
假设 Ki=kj (i与j 都是从1到n,但两者不能同时相等),且在排序前的序列中 Ri领先于 Rj (即
i
后的序列中Rj领先于Rj;, 则称所用的排序方法是不稳定的。注意,排序算法的稳定性是针对所有
记录而言的
关于排序的分类:
关于排序的分类有很多种用法
这里从宏观上讲
主要分为内部排序与外部排序
- 内部排序:待排序记录全部存放在计算机内存中进行排序的过程
- 外部排序:待排序记录的数量很大,以致内存一次不能容纳全部记录, 在排序过程中尚需对外存进行访问的排序过程
内部排序可以分为:
- 插入类:将无序子序列中的一个或几个记录 "插入” 到有序序列中, 从而增加记录的有
序子序列的长度。 主要包括直接插入排序、折半插入排序和希尔排序。 - 交换类:通过 “交换“ 无序序列中的记录从而得到其中关键字最小或最大的记录,并将
它加入到有序子序列中,以此方法增加记录的有序子序列的长度。主要包括冒泡排序和快速排序。 - 选择类:从记录的无序子序列中 ”选择“ 关键字最小或最大的记录,并将它加入到有序子序
列中, 以此方法增加记录的有序子序列的长度。 主要包括简单选择排序、树形选择排序和堆排序。 - 归并类:通过 “归并“ 两个或两个以上的记录有序子序列, 逐步增加记录有序序列的长
度。2-路归并排序是最为常见的归并排序方法。 - 分配类:是唯一一类不需要进行关键字之间比较的排序方法, 排序时主要利用分配和收
集两种基本操作来完成。基数排序是主要的分配类排序方法
以下讲解的算法都是基于顺序表,且都是整数格式
具体定义如下:
可看一下c++的定义结构,其他语言也类似
#define MAXSIZE 20 //顺序表的最大长度
typedef int KeyType; //定义关键字类型为整型
typedef struct{ //关键字项
KeyType key; //其他数据项
InfoType otherinfo; //记录类型
) RedType;
typedef struct{
RedType r[MAXSIZE+1]; //闲置或用做哨兵单元
int length; //顺序表长度
) SqList;
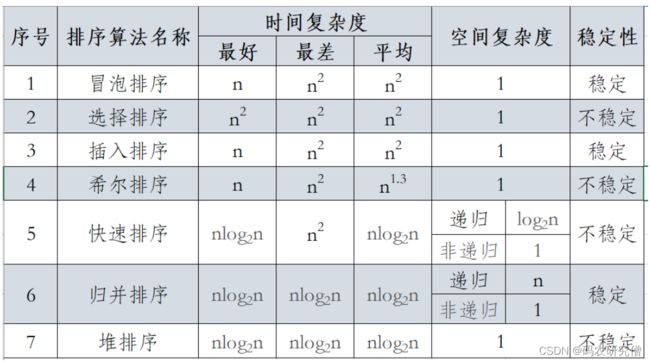
关于排序的评价指标好坏:
分别为时间复杂度和空间复杂度
2. 插入排序
插入排序的基本思想是:每一趟将一个待排序的记录,按其关键字的大小插入到已经排好序的一组记录的适当位置上,直到所有待排序记录全部插入为止
分别为:直接插入排序、折半插入排序和希尔排序
2.1 直接插入排序
将一条记录插入到已排好序的有序表中,从而得到一个新的、 记录数量增1的有序表
i为1到n(不包括n)的范围,则j刚开始的初始为i-1
遍历轮换位置的时候为arr[j + 1] = arr[j];
x为哨兵,存放要插入的值
java版本
public class InsertSort {
public static void sort(int[] arr) {
if (arr.length >= 2) {
for (int i = 1; i < arr.length; i++) {
//挖出一个要用来插入的值,同时位置上留下一个可以存新的值的坑
int x = arr[i];
int j = i - 1;
//在前面有一个或连续多个值比x大的时候,一直循环往前面找,将x插入到这串值前面
while (j >= 0 && arr[j] > x) {
//当arr[j]比x大的时候,将j向后移一位,正好填到坑中
arr[j + 1] = arr[j];
j--;
}
//将x插入到最前面
arr[j + 1] = x;
}
}
}
}
c++版本
void InsertSort(SqList &L)
{//对顺序表L做直接插入排序
for(i=2;i<=L.length;++i){
if(L.r[i].key<L.r[i-1].key) //需将 r[i]插人有序子表
{
L.r[O]=L.r[i]; //将待插人的记录暂存到监视哨中
L.r[i]=L.r[i-1]; //r[i-1]后移
for(j=i-2; L.r[O].key<L.r[j] .key; --j)//从后向前寻找插入位置
{
L.r[j+1]=L.r[j];//记录逐个后移,直到找到插人位置
}
L.r[j+1]=L.r[O];//将 r[O]插人到正确位置
}
}
2.2 折半插入排序
折半查找其实就是在查找插入位置的时候采用二分查找算法
折半插入算法是(直接插入排序+二分查找)
算法思想:
将数据分为有序数据和无序数据
第一次排序时默认Array[0]为有序数据,Array[1]~Array[n-1]为无序数据,有序数据分区的第一个元素位置为low,最后一个元素的位置为high
其逻辑思路写在纸上就是
java版本
import java.util.Arrays;
public class BinaryInsertSort {
//这般插入排序
public static void main(String[] args) {
int[] arr = new int[]{5,1,0,3,4,2,7,9,8,6};
System.out.println("排序之前:"+ Arrays.toString(arr));
binaryInsertSort(arr);
System.out.println("排序之后:"+ Arrays.toString(arr));
}
public static void binaryInsertSort(int[] arr){
int temp;
int low, high, mid;
for (int i = 1; i < arr.length; i++){
temp = arr[i];
low = 0; high = i - 1;
while (low <= high){
mid = (low + high)/2;
if (temp < arr[mid])
high = mid - 1;
else
low = mid + 1;
}
for (int j = i - 1; j >= high + 1; j-- ){
arr[j + 1] =arr[j];
}
arr[high + 1] = temp;
}
}
}
c++版本
void Binsert Sort(SqList &L)
{//对顺序表L做折半插入排序
for (i=2; i < =L. length; ++i)
{
L.r[O]=L.r[i];//将待插人的记录暂存到监视哨中
low=1;high=i-1; //置查找区间初值
while(low<=high)//在r[low .. high]中折半查找插入的位置
{m=(low+high)/2; //折半
if(L.r[O].key<L.r[m].key) high=m-1; //插入点在前一子表
else low=m+1;//插入点在后一子表
}
for (j=i一1;j>=high+1; --j) L.r[j+1]=L.r(j]; //记录后移
L.r[high+1]=L.r[O]; //将r[O]即原r[i], 插入到正确位置
}
}
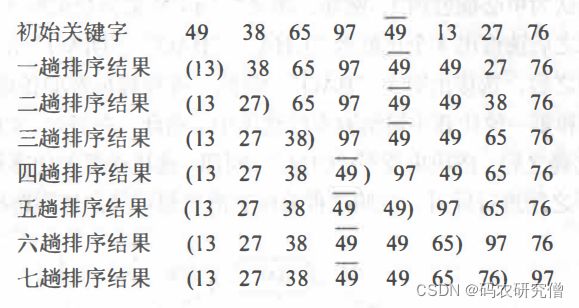
2.3 希尔排序
希尔排序(Shell’sSort)又称 ”缩小增量排序" (Diminishing Increment Sort), 是插入排序的一种
算法思想:
希尔排序实质上是采用分组插入的方法。先将整个待排序记录序列分割成几组,从而减少参与
直接插入排序的数据量,对每组分别进行直接插入排序,然后增加每组的数据量,重新分组。 这样
当经过几次分组排序后,整个序列中的记录 “基本有序” 时,再对全体记录进行一次直接插入排序
希尔对记录的分组,不是简单地 ”逐段分割", 而是将相隔某个 “增量” 的记录分成一组。
非代码演示其逻辑:
- 第一趟取增量 d1 =5 , 所有间隔为 5 的记录分在同一组,全部记录分成 5 组, 在各个组
中分别进行直接插入排序 - 第二趟取增量 d2 = 3, 所有间隔为 3 的记录分在同一组, 全部记录分成 3 组,在各个组
中分别进行直接插入排序 - 第三趟取增量 d3 = 1, 对整个序列进行一趟直接插入排序, 排序完成
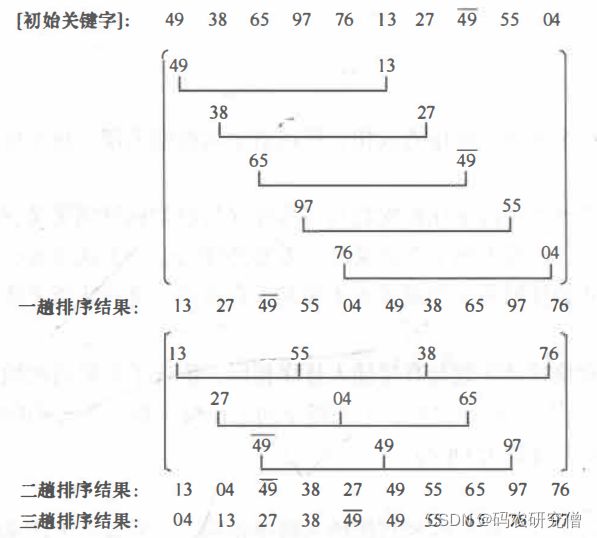
使用三个for
- 最外层for用来做步长的循环判断,并且一半半减半
- 第二层for,如果确定好了步长,第二层for用来确定右区间,并且一步步增长
- 第三层for,也就是内层for,用来确定左区间,并且交换其左右区间,也要一步步和右区间增长
java版本
public static void main(String[] args) {
int arr[] = {7, 5, 3, 2, 4};
//希尔排序(插入排序变种版),i层循环控制步长
for (int i = arr.length / 2; i > 0; i /= 2) {
//j控制无序端的起始位置,并且一步步往右扩充,但不能超过完整长度
for (int j = i; j < arr.length; j++) {
//有区间一步步增长:k=j,左区间一步步增长:k=k-i=j-i=i-i=0;
for (int k = j; k > 0 && k - i >= 0; k -= i) {
if (arr[k] < arr[k - i]) {
int temp = arr[k - i];
arr[k - i] = arr[k];
arr[k] = temp;
} else {
break;
}
}
}
//j,k为插入排序,不过步长为i
}
}
c++版本
void Shellinsert(SqList &L, int dk)
{//对顺序表L做一趟增量是dk的希尔插入排序
for(i=dk+1;i<=L.length;++i)
{
if(L.r[i].key<L.r[i-dk].key) //需将L.r[i]插入有序增扯子表
{
L.r[O]=L.r[i]; //暂存在L.r[O]
for(j=i-dk; j >O&& L.r[O].key<L.r[j].key;j-=dk)
{
L.r[j+dk]=L.r[j];//记录后移, 直到找到插入位置
}
L.r[j+dk]=L.r[O]; //将 r[O]即原r[i], 插入到正确位置
}
}
void ShellSort(SqList &L,int dt[],int t)
{//按增批序列 dt[O .. t-1]对顺序表 L作t 趟希尔排序
for (k=O;k<t;++k) {
Shellinsert(L,dt[k]);//一趟增址为 dt[t]的希尔插入排序
}
}
js版本
此处来源于
舍友的js代码
A = [1, 5, 4, 9, 3, 6, 7, 50, 60, 5, 2];
function shell(A) {
for (let dk = Math.floor(A.length / 2); dk >= 1; dk = Math.floor(dk / 2)) {
for (let i = dk; i < A.length; i++) {
let k = i;
let temp = A[k];
while (temp < A[k - dk] && k > 0) {
A[k] = A[k - dk];
k = k - dk;
}
A[k] = temp;
}
}
return A;
}
console.log(shell(A));
3. 交换排序
交换排序的基本思想是:两两比较待排序记录的关键字,一旦发现两个记录不满足次序要求时则进行交换,直到整个序列全部满足要求为止
3.1 冒泡排序
冒泡排序(Bubble Sort)是一种最简单的交换排序方法,它通过两两比较相邻记录的关键字,如果发生逆序,则进行交换,从而使关键字小的记录如气泡一般逐渐往上 "漂浮"(左移),或者使关键字大的记录如石块一样逐渐向下 "坠落”(右移)
java版本
- 右移的版本,也就是先放最大的数字
外层循环控制循环的次数,一次次缩小,没有自身
内层循环控制循环的个数,随着外层循环的增加,内层循环会越来越小
类似这种数字
public static void main(String[] args) {
int arr[] = {4,5,6,3,2,1};
//冒泡
for (int i = 0; i < arr.length-1; i++) {
//外层循环,遍历次数
for (int j = 0; j < arr.length - i - 1; j++) {
//内层循环,升序(如果前一个值比后一个值大,则交换)
//内层循环一次,获取一个最大值
if (arr[j] > arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
- 左移版本,先弄最小数字
外层循环时0到n-1,因为时比较最小数字,所以要留一个数字和右边的比较,不能是n与自已比较,是n-1与n比较
内层循环是比较
int arr[] = {4,5,6,3,2,1};
int b =0;
for(int i=arr.length;i>1;i--) { //从大开始循环 从后面开始比较
for(int j=0;j<i-1;j++) {
if(arr[j]<arr[j+1]) {
b=arr[j];
arr[j]=arr[j+1];
arr[j+1]=b;
}
}
}
- 进化版
加入一个布尔变量,如果内循环没有交换值,说明已经排序完成,提前终止
public static void sortPlus(int[] arr){
if(arr != null && arr.length > 1){
for(int i = 0; i < arr.length - 1; i++){
// 初始化一个布尔值
boolean flag = true;
for(int j = 0; j < arr.length - i - 1 ; j++){
if(arr[j] > arr[j+1]){
// 调换
int temp;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
// 改变flag
flag = false;
}
}
if(flag){
break;
}
}
}
}
c++版本
void BubbleSort(SqList &L)
{//对顺序表L做冒泡排序
m=L.length-1;flag=1; //flag用来标记某一趟排序是否发生交换
while ((m>O) && (flag==1))
{
flag=O; //flag置为0, 如果本趟排序没有发生交换,则不会执行下一趟排序
for (j=1;j<=m;j++)
{
if(L.r[j].key>L.r[j+1].key)
{
flag=1; //flag置为1, 表示本趟排序发生了交换
t=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=t;//交换前后两个记录
} //if
m--;
}
}
3.2 快速排序
快速排序 (Quick Sort) 是由冒泡排序改进而得的。 在 冒泡排序过程中, 只对相邻的两个记录进行比较, 因此每次交换两个相邻记录时只能消除一个逆序。 如果能通过两个(不相邻)记录的一次交换,消除多个逆序, 则会大大加快排序的速度。 快速排序方法中的一次交换可能消除多个逆序
算法思想:
在待排序的 n个记录中任取一个记录(通常取第一个记录)作为枢轴(或支点),设其关键字为
pivotkey。经过一趟排序后,把所有关键字小千pivotkey 的记录交换到前面,把所有关键字大于pivotkey
的记录交换到后面,结果将待排序记录分成两个子表,最后将枢轴放置在分界处的位置。然后,分别
对左、右子表重复上述过程,直至每一子表只有一个记录时,排序完成
具体步骤如下:
- 选择待排序表中的第一个记录作为枢轴,将枢轴记录暂存在 r[0]的位置上。附设两个指针 low
和 high, 初始时分别指向表的下界和上界(第一趟时, low = 1; high= L.length;)。 - 从表的最右侧位置依次向左搜索 ,找到第一个关键字小于枢轴关键字 pivotkey 的记录,将其移到 low 处。具体操作是:当 low
- 然后再从表的最左侧位置,依次向右搜索找到第一个关键字大于 pivotkey 的记录和枢轴记录交换。具体操作是:当 low
- 重复步骤2和3, 直至 low 与 high 相等为止。此时 low 或 high 的位置即为枢轴在此趟排序中的最终位置, 原表被分成两个子表
- 然后再从表的最左侧位置,依次向右搜索找到第一个关键字大于 pivotkey 的记录和枢轴记录交换。具体操作是:当 low
注意事项
一定要移动j在移动i。
不能先移动i指针,如果本身是已经排序好的序列,那么i就直接移动到最后一格停止,然后arr[low]和arr[i]再交换就错了。而先移右边,即使j直接移到了第一个low,那么arr[low]和arr[i]就是同一个元素,交换也没影响

另一种算法,通俗易懂的算法步骤:
-
设置两个指针left和right分别指向数组的头部和尾部,并且以头部的元素为基准数
-
right指针先往左移动,找到小于基准数的元素就停下,然后准备移动left指针
-
left指针往右移动,找到大于基准数的元素就停下,然后交换right和left指针所值元素的值
重复第二、三步,直到两个指针left和right重合
- 两个指针重合后将基准数与两个指针指向的元素值交换
java版本
public class QuickSort {
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return;
}
i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i<j) {
//先看右边,依次往左递减
while (temp<=arr[j]&&i<j) {
j--;
}
//再看左边,依次往右递增
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
public static void main(String[] args){
int[] arr = {10,7,2,4,7,62,3,4,2,1,8,9,19};
quickSort(arr, 0, arr.length-1);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
c++版本
int Partition(SqList &L, int low, int high)
{//对顺序表1中的子表r[low .. high)进行一趟排序,返回枢轴位置
L.r[O]=L.r[low]; //用子表的第一个记录做枢轴记录
pivotkey=L.r[low].key; //枢轴记录关键字保存在pivotkey中
while(low<high) //从表的两端交替地向中间扫描
{
while(low<high&&L.r[high] .key>=pivotkey) --high;
L.r[low]=L.r[high]; //将比枢轴记录小的记录移到低端
while(low<high&&L.r[low].key<=pivotkey) ++low;
L.r[high)=L.r[low] ; //将比枢轴记录大的记录移到高端
}
L.r[low] =L.r[O];//枢轴记录到位
return low;//返回枢轴位置
}
void QSort(SqList &L,int low,int high)
(//调用前置初值: low=1; high=L.length;
//对顺序表L中的子序列L.r[low .. high]做快速排序
if(low<high) { //长度大于1
pivotloc=Partition (L, low, high); //将L.r[low.. high] 一分为二,pivotloc是枢轴位置
QSort(L, low, pivotloc-1); //对左子表递归排序
QSort (L, pivotloc+1, high); //对右子表递归排序
}
}
void QuickSort(SqList &L)
{//对顺序表L做快速排序
QSort(L,1,L.length);
}
4. 选择排序
选择排序的基本思想是:每一趟从待排序的记录中选出关键字最小的记录,按顺序放在已排序的记录序列的最后,直到全部排完为止
4.1 简单选择排序
简单选择排序 (SimpleSelection Sort)也称作直接选择排序
算法思想:
- 设待排序的记录存放在数组r[l… n]中。第一趟从r[I]开始,通过n-1次比较,从n个记录中选出关键字最小的记录,记为r[k], 交换r[l]和r[k]。
- 第二趟从r[2]开始,通过n-2次比较,从n-1个记录中选出关键字最小的记录,记为r[k],交换r[2]和r[k]
- 依次类推,第i趟从r[i]开始,通过n-i次比较,从n-i+l个记录中选出关键字最小的记录,记为r[k], 交换r[i]和r[k]。
- 经过n-1趟,排序完成。
int min;//将当前的i暂定为是最小的数的位置
int tmp;//用于交换
for (int i = 0; i < a.length; i++) {
min= i;
for (int j = i + 1; j < a.length; j++) {
if (a[min] > a[j]) {
min = j;//把较小的数放到前面,但是目前仍未进行交换,因为还没有找出最小的那个数
}
}
tmp = a[min];
a[min] = a[i];
a[i] = tmp;
}
c++版本
void SelectSort(SqList &L)
{//对顺序表L做简单选择排序
for(i=1;i<L.length;i++){//在L.r[i. .L. length]中选择关键字最小的记录
k=i;
for (j=i+1; j<=L.length; ++j) {
if(L.r[j].key<L.r[k].key) k=j;
} //k指向此趟排序中关键字最小的记录
if (k!=i)
{t=L.r[i]; L.r[i)=L.r[k]; L.r[k]=t;} //交换r[i]与r[k]
}
}
4.2 堆排序
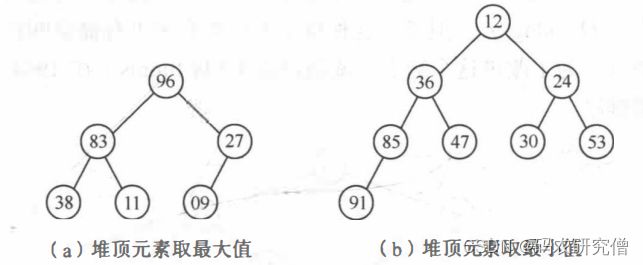
堆排序 (Heap Sort) 是一种树形选择排序,在排序过程中,将待排序的记录 r[l…n]看成是一棵完全二叉树的顺序存储结构,利用完全二叉树中双亲结点和孩子结点之间的内在关系,在当前无序的序列中选择关键字最大(或最小)的记录
顾名思义, 就是将数据以堆的结构, 或者说类似于二叉树的结构, 每次都整理二叉树将最大值或者最小值找到, 然后放到数组末尾
显然,在这两种堆中 ,堆顶元素(或 完全二叉树的根)必为序列中 n个元素的最大值(或最小值),分别称之为大根堆和小根堆
5. 归并排序
归井排序(Merging Sort)就是将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并成一个有序表的过程称为2-路归井,2-路归并 最为简单和常用
基本思想其实就是分治算法,将待排序元素分成大小大致相同的2个子集合,分别对2个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
整体代码思路如下
这是分治的”治“算法部分逻辑

所谓的“治”算法 非代码演示如下

java版本
public class Main {
public static void main(String[] args) {
int[] arr = {11,44,23,67,88,65,34,48,9,12};
int[] tmp = new int[arr.length]; //新建一个临时数组存放
mergeSort(arr,0,arr.length-1,tmp);
for(int i=0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
public static void merge(int[] arr,int low,int mid,int high,int[] tmp){
int i = 0;
int j = low,k = mid+1; //左边序列和右边序列起始索引
while(j <= mid && k <= high){
if(arr[j] < arr[k]){
tmp[i++] = arr[j++];
}else{
tmp[i++] = arr[k++];
}
}
//若左边序列还有剩余,则将其全部拷贝进tmp[]中
while(j <= mid){
tmp[i++] = arr[j++];
}
while(k <= high){
tmp[i++] = arr[k++];
}
for(int t=0;t<i;t++){
arr[low+t] = tmp[t];
}
}
public static void mergeSort(int[] arr,int low,int high,int[] tmp){
if(low<high){
int mid = (low+high)/2;
mergeSort(arr,low,mid,tmp); //对左边序列进行归并排序
mergeSort(arr,mid+1,high,tmp); //对右边序列进行归并排序
merge(arr,low,mid,high,tmp); //合并两个有序序列
}
}
}
c++版本
void Merge{RedType R[],RedType &T[],int low,int mid,int high)
{//将有序表 R[low.. mid]和R[mid+l. .high]归并为有序表 T[low.. high]
i=low;j=mid+l;k=low;
while(i<=mid&&j<=high) //将R中记录由小到大地并入T中
{
if (R[i].key<=R[j].key) T[k] =R[i++];
else T[k)=R[j++];
}
while(i<=mid) T[k++]=R[i++]; //将剩余的 R[low.. mid]复制到 T中
while (j<=high) T [k++]=R[j++]; //将剩余的 R[j.high]复制到 T 中
}