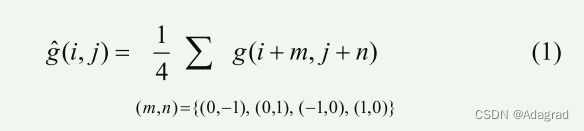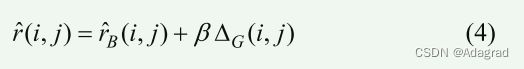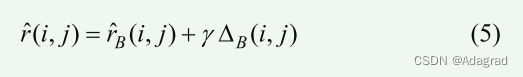HIGH-QUALITY LINEAR INTERPOLATIONFOR DEMOSAICING OF BAYER-PATTERNED COLOR IMAGES

ABSTRACT

本文介绍了一种新的插值技术，用于对单 CCD 数码相机生成的彩色图像进行去马赛克。我们表明，与双线性去马赛克相比，所提出的简单线性滤波器可以使 PSNR 提高超过 5.5 dB，与最近引入的线性插值器相比，R 和 B 插值可提高约 0.7 dB。所提出的滤波器还优于大多数非线性去马赛克算法，没有由于非线性处理而产生的伪影，并且大大降低了计算复杂性。

1. INTRODUCTION

数码相机如今非常流行。许多用户正在放弃常规的胶片摄影。为了降低成本，大多数数码相机使用单个电荷耦合器件 (CCD) 传感器，在光路中的 CCD 像素之前是拜耳马赛克图案的滤色器阵列 (CFA)，如图 1 所示。每组 2×2 像素中，两个对角相对的像素具有绿色滤光片，另外两个像素具有红色和蓝色滤光片。由于G携带了人类的大部分亮度信息，因此其采样率是R和B的两倍。

我们将去马赛克称为对 CFA 捕获的图像进行插值的问题，这样对于每个 CCD 像素，我们都可以关联一个完整的 RGB 值。最简单的去马赛克方法是双线性插值 [1]–0，其中三个颜色平面使用对称双线性插值从相同颜色的最近邻独立插值。正如预期的那样，双线性插值会产生明显的伪影，尤其是在边缘和其他高频内容上，因为它没有考虑 RGB 值之间的相关性。实用的去马赛克算法将这种相关性纳入考虑范围，要么使用更好的线性滤波器[4]，要么使用使插值平滑度适应图像活动或边缘度[1]–0的非线性滤波器。

在本文中，我们提出了一种简单的线性去马赛克滤波器，与[4]中的滤波器相比，具有更好的性能和更低的复杂性。我们的滤波器还优于许多非线性算法。在第 2 节中，我们快速回顾了一些为改进去马赛克性能而提出的技术，在第 3 节中，我们介绍了新的线性滤波器。第 4 节和第 5 节分别介绍了性能比较和结论。

2. BEYOND BILINEAR DEMOSAICING

参考图1，在双线性马赛克中，红色或蓝色像素处的像素位置(i,j)的绿色值g(i,j)，是通过交叉图中相邻绿色值的平均值来计算的:

对应于将图1中标记为“+”的像素处的绿色值估计为观察到的标记为“·”的绿色值的平均值。在图像边界处，只包含位于图像内的像素，并调整缩放。对于R和B颜色，同样的方程适用(具有对角交叉模式)，除了对于位于绿色像素中的像素位置(i,j)，只有两个相邻的红色值被平均以产生一个插值的红色值;蓝色也是如此。(1)除了计算简单外，它的输出值保证与输入值具有相同的动态范围，因此输出值不需要溢出逻辑。

利用 RGB 通道之间的相关性是提高去马赛克性能的主要思想。具体来说，我们可以假设在亮度/色度分解中，色度分量在像素之间变化不大。在 Freeman [2]、[5] 的恒定色调方法中，对绿色通道进行双线性插值，然后对 R 和 B 通道进行插值，以保持恒定色调，定义为 R/G 和 B/G比率。即使以计算这些除法为代价，它仍然会产生可见的伪影 [2]。通过从双线性插值 G 像素开始，并对色差 R – G 和 B – G 的插值应用中值滤波器，可以获得更好的结果 [2]。

使用基于梯度的方法[2]、[6]可以获得改进的性能，这些方法通常估计边缘方向并调整插值公式，以便优先沿着边缘方向而不是跨边缘方向执行滤波。例如，在Laroche和Prescott方法中插值绿色通道时，R和B通道用于确定边缘方向，这为绿色通道确定了与(1)中的项不相等的权重；然后对色差 R–G 和 B–G 进行插值 [2],[6]。 Hamilton 和 Adams 的方法通过考虑一阶和二阶像素差异来改进 Laroche 和 Prescott 的方法 [6],[7]。 Chang、Cheung 和 Pang 通过考虑可变数量的梯度对此进行了改进 [8]。 [9]中提出了一种更简单但有效的算法，它使用软决策规则来组合水平和垂直方向的插值结果。

迭代方法可以通过使用 B 和 R 插值的结果来校正 G 插值来进一步改进，反之亦然。这是 Kimmel 方法 0 的基础，其中插值步骤基于恒定色调和基于梯度的方法的组合。 [6] 中提出了一种基于迭代投影的技术。它在一组流行的标准测试图像上具有迄今为止最好的性能，但它具有非常高的复杂性（每个输入像素多达 480 次操作）。因此，[6]中的方法可以被视为将性能界限设置为更实用的算法可以实现的性能。

3. IMPROVED LINEAR INTERPOLATION

有趣的是，上一节讨论的大多数算法都使用非线性滤波器，其支持区域超出直接相邻的像素。这就提出了一个简单的问题，[1]–0、[5]–[9] 中没有解决这个问题：我们可以从支持区域延伸到 5×5 的线性滤波器中获得的最佳性能是什么？像素区域？

Pei 和 Tam 沿着这些思路提出了一个很好的解决方案 [4]，首先通过双线性插值估计 R 和 G，然后估计这些颜色差异 B – G 和 R – G，通过 4 点平均值平滑颜色差异（在假设色差缓慢变化），最后使用这些值来插值 G 值，然后对 R 和 B 值进行最终估计。它们展开的插值方程相当于在当前像素周围的 5x5 像素窗口上运行的线性滤波器 [4]。

3.1 The Proposed Interpolation Method

我们建议使用以下标准，而不是像上述方法那样使用恒定或接近恒定的色调方法：边缘的亮度比色度分量强得多。因此，例如，当我们在红色像素位置处查看绿色值的插值时，我们不会丢弃该位置处的红色值 - 这是有价值的信息！相反，我们将该红色值与最近红色样本的双线性插值的估计值进行比较。如果与该估计值不同，则可能意味着该像素处存在急剧的亮度变化，因此我们通过添加该估计亮度变化的一部分来校正双线性插值的绿色值。

具体来说，例如，要在 R 位置插值 G 值（图 1 中的“+”像素），我们使用以下公式

(2)中的下标B表示双线性插值，如(1)。因此，我们通过测量像素位置处已知颜色的梯度 ΔR 来校正双线性插值估计，这是通过（3）中的简单公式估计的。增益因子α控制这种校正的强度。

因此，我们的方法实际上是一种梯度校正双线性插值方法，具有增益参数来控制应用多少校正。对于在蓝色像素处插值 G，使用相同的公式，但通过 ΔB(i,j) 进行校正。为了在绿色像素处插值 R，我们使用以下公式

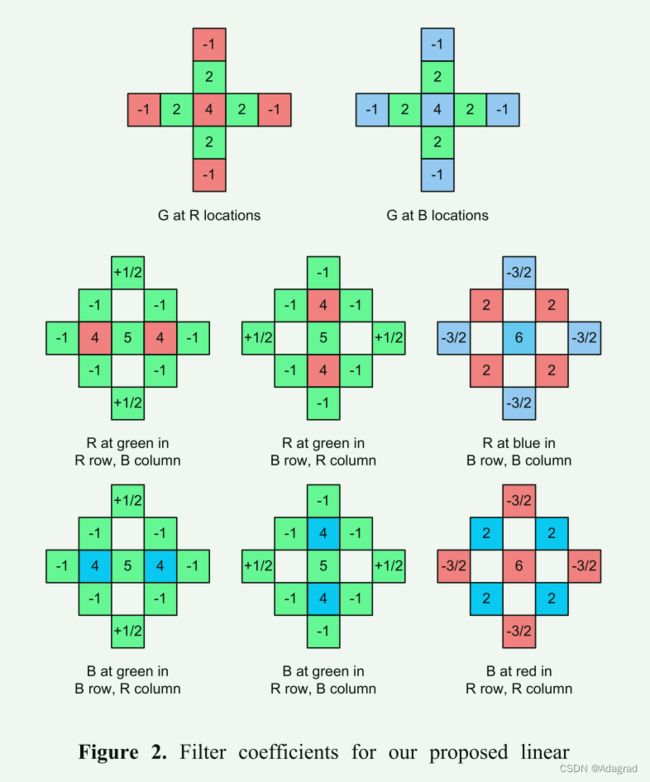
ΔG(i,j) 由 9 点区域确定，如图 2 所示。为了在蓝色像素处插值 R，我们使用以下公式

ΔB(i,j) 在 5 点区域上计算，如图 2 所示。根据对称性，插值 B 的公式类似。

3.2 Gradient-Correction Gains

为了确定增益参数 {α,β,γ} 的适当值，我们使用了维纳方法；也就是说，我们计算了导致最小均方误差插值的值，给定从良好数据集（[6]中使用的柯达图像集）计算出的二阶统计量。然后我们用1/2小幂的整数倍来近似最优维纳系数，最终结果α = 1/2，β = 5/8，γ = 3/4。根据 {α,β,γ} 的值，我们可以计算每个插值情况的等效线性 FIR 滤波器系数。如图 2 所示，所得系数值使滤波器非常接近 5×5 支持区域的最佳维纳滤波器（均方误差在 5% 以内）。

因此，我们认为设计具有较低均方插值误差的实用线性滤波器的唯一方法是使用更大的支持区域。这不仅会增加计算复杂性和内存占用，还会导致边缘周围出现振铃伪影。

评估计算复杂度的一种方法是计算 5×5 支持区域内非零滤波器系数的数量。对于 Pei-Tam 的方法 [4]，G 通道有 9 个非零系数，R 和 B 通道平均各有 13 个。我们的方法的复杂度稍低：G 通道有 9 个系数，R 和 B 通道各有 11 个系数。

4. PERFORMANCE

我们将我们提出的方法与其他几种方法进行了比较，使用柯达图像集 [6]，通过模拟拜耳采样阵列（简单地通过为每个像素仅保留每个 RGB 值之一，如图 1 所示），然后应用各种插值算法。这种子采样方法并不真正代表数码相机，数码相机通常采用仔细的镜头设计来有效地执行少量低通滤波，以减少由于拜耳模式子采样而导致的混叠。然而，由于参考文献中的所有论文都只执行子采样，没有低通滤波，所以我们做了同样的事情，以便我们可以比较结果。我们还在拜耳二次采样之前使用少量高斯低通滤波测试了所有插值方法，发现无论有没有滤波，这些方法的相对性能大致相同。表 1 显示了双线性插值法在峰值信噪比 (PSNR) 方面的改进。除了 Freeman 方法之外，大多数方法都带来了超过 5 dB 的改进，并且我们提出的方法平均优于所有其他方法。

除了 PSNR 测量之外，我们还需要验证视觉质量。图 3 显示了柯达集中一张图像的插值结果。从这些结果中我们可以看出，我们提出的方法的质量类似于 Kimmel 0 等良好的非线性方法，但复杂性要低得多。与 Pei-Tam 线性滤波器相比，我们的方法产生的色边失真稍显不明显，并且 PSNR 较低，计算复杂度也略有降低。

5. CONCLUSION

我们提出了一种新的去马赛克方法，用于使用拜耳滤色器阵列对从单个 CCD 捕获的图像进行颜色插值。所提出的线性滤波器在维纳意义上几乎是最优的，并且实际上优于许多更复杂的非线性滤波器。与最近推出的线性去马赛克方法 [4] 相比，我们的滤波器使插值图像质量提高了 0.5 dB（均方误差降低了 12%），这是由于绿色通道的质量相同且提高了约 0.7 dB对于 R 和 B 通道。与[4]相比，我们的方法还导致计算复杂度小幅降低（大约12%）。