回溯算法问题个人感悟--包含剪枝问题(基于力扣-c++版)
回溯法也可以叫做回溯搜索法,它是采用递归的一种穷举搜索的方式。
至于为啥需要回溯,直接for循环遍历穷举不就完事了。。但是有时候你并不知道for循环有几层,或者for循环太多,写起来太费事,但是能发现没层for循环都有一定的可以规律,比如第一此需要从10个鸡蛋挑一个,第二次需要从剩余9个鸡蛋再挑一个,依次类推,凡是拥有可递归规律的问题都可以采用回溯法。
目录
回溯过程与模板
感悟1:关于模板中本层for循环的书写
理解2:剪枝不同情况及三种方法
回溯过程与模板
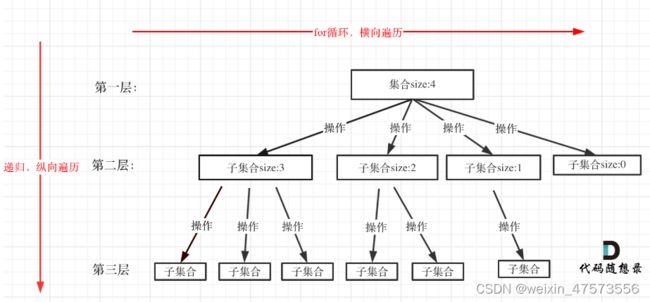
一般回溯都是树形结构,毕竟是基于递归
如何完成穷举,即在相同状态下每一次选择时遍历每一种可能(即下面的树层的横向for操作),在状态改变后的遍历则交给递归去做(即下面的纵向树枝操作)
这树层与树枝两个概念需要理解,接下来将由此展开
代码模板如下:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}经典回溯题型:力扣
感悟1:关于模板中本层for循环的书写
对于这题:力扣
我的解答如下:
class Solution {
public:
set path;
set> result;
int Get(vector& candidates, int target,int cur){
if(cur==target){
result.insert(path);
return 0;
}
else if(cur>target)
return 1;
else{
for(int i=0;i> combinationSum(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
Get(candidates,target,0);
vector> res(result.begin(),result.end());
return res;
}
}; 别人的解答:
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
return;
}
// 如果 sum + candidates[i] > target 就终止遍历
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i);
sum -= candidates[i];
path.pop_back();
}
}
public:
vector> combinationSum(vector& candidates, int target) {
result.clear();
path.clear();
sort(candidates.begin(), candidates.end()); // 需要排序
backtracking(candidates, target, 0, 0);
return result;
}
}; 在对于树层的for循环书写中,我的理解很直接,既然次数不限制,即每一次都可以选择任一数,所以下标从0开始遍历就行,但是其他人的回溯则对数组遍历有了起始下标,一开始没有理解其思想.
例如给样例 [2,3,6,7],这样第二层就只能从选择3,6,7,无法选择2,这样会不会漏掉答案,起始回溯的本质就是穷举,只要能遍历所有可能即可,因为答案是无序的,所以包含有2的答案别人在第一层循环中就已经遍历了所有的可能,这样在后续的数层中就可以遍历不包含2的情况,其实也是穷举了所有可能。
只要可以穷举则行得通,甚至有的题目不用for循环也可以,例如我的以下解答:
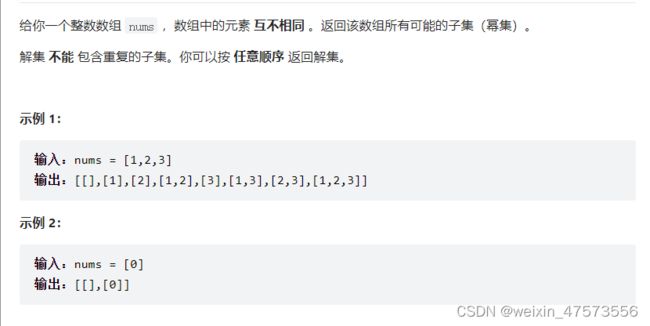
子集题目1:力扣
class Solution {
public:
vector> result;
vector path;
void Get(vector& nums,int k){
if(k==nums.size()){
result.push_back(path);
return;
}else{
path.push_back(nums[k]);
Get(nums,k+1); //选了当前元素
path.pop_back();
Get(nums,k+1); //没选当前元素
}
return;
}
vector> subsets(vector& nums) {
Get(nums,0);
return result;
}
}; 可以看出,这题我连for循环都没有使用,因为我做这题的思想是子集就是遍历每一个元素,每个元素的选择只有两种可能,一种是子集中有这个元素,一种是没有这个元素,故不需要for循环。
但是之所以模板给的有for循环,其实还是有尽量在一层中可以遍历所有元素会好一点,因为可以进行剪枝,例如下题:
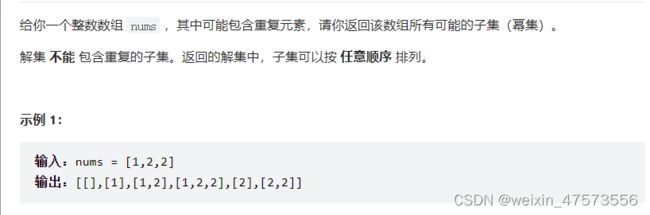
子集题目2:力扣
这题,给的数组元素可以重复,如果像我之前那样写,则不容易进行剪枝,只能对结果进行去重,但是这样效率低,很容易超时,规范解答如下:
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex) {
result.push_back(path);
unordered_set uset;
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector> subsetsWithDup(vector& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 去重需要排序
backtracking(nums, 0);
return result;
}
}; 可以看到,整体做题思想没变的前提下(就是对于某个元素,子集中有它或没有它两种情况遍历),改写成for循环形式,通过在树层中遍历每一个元素(在同一层中遍历到某个元素,则代表当前递归的这个子集,在该元素之前的元素都没选),从而实现对所有情况的遍历。
并且有了for循环后方便剪枝,该题就是通过set进行树层级别的剪枝,具体剪枝方法下面介绍,这里只需知道在树层级别遍历元素可以方便剪枝即可。
理解2:剪枝不同情况及三种方法
没有剪枝的回溯就是穷举,优秀的剪枝操作不仅省时,并且有时也方便满足题目的需求。
以上面的提到过的子集问题2为例:
1、首先最为推荐的的就是使用used数组去重:
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex, vector& used) {
result.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 而我们要对同一树层使用过的元素进行跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, i + 1, used);
used[i] = false;
path.pop_back();
}
}
public:
vector> subsetsWithDup(vector& nums) {
result.clear();
path.clear();
vector used(nums.size(), false);
sort(nums.begin(), nums.end()); // 去重需要排序
backtracking(nums, 0, used);
return result;
}
}; 这也是最可以在多种问题上复制的套路,就是创建一个used数组,通过判断used[i]是false还是true从而判断是否跳过这个元素实现去重,剪枝等。这个方法要好好理解:
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
这里比价抽象,因为初始化为false,而每一次回溯则将used[i]转为false,故相当于同一层中前面相同值为false,则代表已经遍历过这种情况了故跳过,而若对树枝剪枝,则判断used[i]是否为true(这里只是一个方便的点,假如有需要的话,一般树枝去重需要自己根据具体情况写不同代码,这里有used数组主要是方便具体操作)。
这里需要对递归有一定理解,所有的遍历+递归情况都对同一used数组进行操作,只不过在不同时间中used数组因为递归+回溯而一直在改变。
2、使用set进行去重
这个方法的代码在前面已经展示过了,这里方便比较,再展示一下,思想和used一样,同一层出现的元素则不再使用,故自然联想到使用set集合存储判断
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex) {
result.push_back(path);
unordered_set uset;
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector> subsetsWithDup(vector& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 去重需要排序
backtracking(nums, 0);
return result;
}
}; 3、使用下标剪枝
这也是最为简便的一种剪枝方式,用于树层去重,其思想相同,但是应用范围比较小
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex) {
result.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
while(i+1> subsetsWithDup(vector& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 去重需要排序
backtracking(nums, 0);
return result;
}
}; 其实这三种方法在树层中剪枝的思想一样,但是之所以介绍三种是因为不同的使用场景可能会发挥不一样的作用,例如used可以进行树枝剪枝,而下标剪枝则必须要排序(有的题目不能排序)
总体来说这三种方法的适用场景范围:
used数组剪枝 > set剪枝 > 下标剪枝
本文内容素材基于代码随想录