Bellman_Ford算法---最短路问题

算法模板：

 例题：AcWing 853有边数限制的最短路：

给定一个 n 个点 mm条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k条边的最短距离，如果无法从 1号点走到 n号点，输出 impossible。

数据范围

1≤n,m≤10^5 1≤n,m≤10^5,
图中涉及边长绝对值均不超过 1000010000。

for (int i = 1; i <= k; i++)
    {
        memcpy(backup, dis, sizeof dis);
        for (int j = 1; j <=m; j++)
        {

            int b = edge[j].b, a = edge[j].a, w = edge[j].w;
            if (dis[b] > (backup[a] + w))dis[b] = backup[a] + w;
        }
    }

1.（外重循环）循环i从1到n，遍历n次指的：是不经过i条边到达终点的最短距离

经过n次操作n个点的最短距离也就确定了；

2.（内重循环）循环j从1到m，遍历m条边，把所有边都进行松弛操作；

每次取出两点以及他们连接的边的权重（a,b,w表示a—>b的一条边）；

用从起点到a的当前最短距离+权重来更新从起点到b的当前最短距离；

最短距离的原理：第二重循环遍历了m条边，每条都被遍历了n次；

所以这n个点的所有他的前驱后继相对应的边权一定都被遍历到了

又因为他是有松弛操作的，所以只要上一个点（前驱）的当前最短路求出来了

这个点就可以用他的前驱来更新他的最短距离，从而他的后继又可以用它来更新最短距离了。

PS：backup数组用来防止串联 memcpy备份：只用上一次迭代的结果

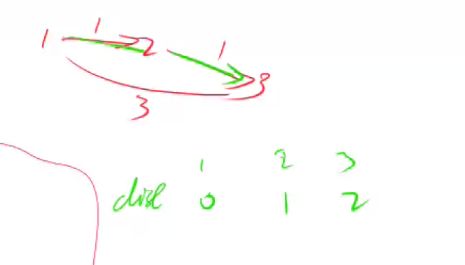
 样例中k的限制是1，在此限制下的最短距离因为为3，但是因为串联(用二重循环中本次更新的2结点)来更新节点3的距离，导致最短路错为2。

#include
#include

using namespace std;
const int N = 520;
const int M = 100000;
int n, m, k, dis[N], backup[N];

struct edge {
    int a, b, w;
}edge[M];

void bellman_ford()
{
    memset(dis, 0x3f, sizeof dis);
    dis[1] = 0;
    for (int i = 1; i <= k; i++)
    {
        memcpy(backup, dis, sizeof dis);
        for (int j = 1; j <=m; j++)
        {

            int b = edge[j].b, a = edge[j].a, w = edge[j].w;
            if (dis[b] > (backup[a] + w))dis[b] = backup[a] + w;
        }
    }
    if (dis[n] > 0x3f3f3f3f / 2)cout << "impossible";
//这里除以2的原因是：如果图中存在负权，用距离是正无穷的点来更新下一个点时，会在
//正无穷上减去负权值，所以我们用一个小于正无穷的较大数来判断是不是满足条件
    else cout << dis[n];
}
int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++)
    {
        cin >> edge[i].a >> edge[i].b >> edge[i].w;
    }
    bellman_ford();

}

注释的举例：

借鉴于AcWing 853. 有边数限制的最短路 - AcWing