leetcode 数组
数组
统计系列
有效数独
按行枚举,按列枚举,按方格枚举
bool isValidSudoku(vector<vector<char>>& g) {
bool st[9];
// 行枚举
for (int i = 0; i < 9; i++) {
memset(st, 0, sizeof(st));
for (int j = 0; j < 9; j++) {
if (g[i][j] != '.') {
int t = g[i][j] - '1';
if(st[t]) return false;
else st[t] = true;
}
}
}
// 列枚举
for (int i = 0; i < 9; i++) {
memset(st, 0, sizeof(st));
for (int j = 0; j < 9; j++) {
if (g[j][i] != '.') {
int t = g[j][i] - '1';
if(st[t]) return false;
else st[t] = true;
}
}
}
// 方块枚举
for (int i = 0; i < 9; i += 3) {
for (int j = 0; j < 9; j += 3) {
memset(st, 0, sizeof(st));
for (int x = 0; x < 3; x++) {
for (int y = 0; y < 3; y++) {
if (g[i + x][j + y] != '.') {
int t = g[i + x][j + y] - '1';
if(st[t]) return false;
else st[t] = true;
}
}
}
}
}
return true;
}
甲板上的战舰
只需要记录左上角 x 的数量
int countBattleships(vector<vector<char>>& g) {
int res = 0;
for (int i = 0; i < g.size(); i++) {
for (int j = 0; j < g[0].size(); j++) {
if (i > 0 && g[i - 1][j] == 'X') continue;
if (j > 0 && g[i][j - 1] == 'X') continue;
if (g[i][j] == 'X') res++;
}
}
return res;
}
矩阵置 0
用第一行记录所有列上是否有 0
用第一列记录所有行上是否有 0
只需再开辟两个变量记录第一行和第一列是否有 0
void setZeroes(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
int row = 1, col = 1;
// 用两个变量记录第一行和第一列是否有 0
for (int i = 0; i < m; i++) if (!g[0][i]) row = 0;
for (int i = 0; i < n; i++) if (!g[i][0]) col = 0;
// 用第一行记录所有列上是否有 0
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++)
if (!g[j][i]) g[0][i] = 0;
}
// 用第一列记录所有行是否有 0
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++)
if (!g[i][j]) g[i][0] = 0;
}
// 用第一行的记录回填列
for (int i = 1; i < m; i++) {
if (!g[0][i])
for (int j = 1; j < n; j++) g[j][i] = 0;
}
// 用第一列的记录回填行
for (int i = 1; i < n; i++) {
if (!g[i][0])
for (int j = 1; j < m; j++) g[i][j] = 0;
}
// 用两个单独记录第一行第一列的变量回填第一行和第一列
if (!row) for (int i = 0; i < m; i++) g[0][i] = 0;
if (!col) for (int i = 0; i < n; i++) g[i][0] = 0;
}
最小操作次数使数组元素相等
曲线救国方式:除选择的元素增加 1 -> 选择的元素 -1
只需要把所有元素降到最小值即可,所以只需要关注当前值 - 最小值
int minMoves(vector<int>& a) {
int minv = INT_MAX, res = 0;
for (auto x : a) minv = min(minv, x); // 求最小值
for (auto x : a) res += x - minv; // 当前元素移动次数 = 当前值 - 最小值
return res;
}
数组拆分 I
min(ai, bi) 总和最大 -> ai 和 bi 尽可能相等 -> 排序即可
因为排序了,所以前一个元素肯定比后一个元素小
int arrayPairSum(vector<int>& a) {
sort(a.begin(), a.end());
int res = 0;
for (int i = 0; i < a.size() - 1; i+= 2) res += a[i];
return res;
}
区间系列
区间合并
先按照左端点排序,有交集更新端点,无交集开辟区间
vector<vector<int>> merge(vector<vector<int>>& is) {
vector<vector<int>> res;
if (is.empty()) return res;
sort(is.begin(), is.end());
int l = is[0][0], r = is[0][1];
for (int i = 1; i < is.size(); i++) {
// 有交集更新端点
if (r >= is[i][0]) r = max(r, is[i][1]);
// 无交集开辟区间
else {
res.push_back({l, r});
l = is[i][0], r = is[i][1];
}
}
res.push_back({l, r});
return res;
}
插入区间
vector<vector<int>> insert(vector<vector<int>>& a, vector<int>& b) {
vector<vector<int>> res;
int i = 0, n = a.size();
// 1. 前面无交集部分,直接添加
while (i < n && a[i][1] < b[0]) res.push_back(a[i++]);
// 2. 有交集部分,扩展
if (i < n) {
b[0] = min(b[0], a[i][0]);
while (i < n && a[i][0] <= b[1]) b[1] = max(b[1], a[i++][1]);
}
res.push_back(b);
// 3. 后面无交集部分,直接添加
while (i < n) res.push_back(a[i++]);
return res;
}
摩尔投票
多数元素
摩尔投票法简化版:肉搏一换一,人多的一方绝对会胜利。胜利方最少比对方多一
int majorityElement(vector<int>& a) {
int res = a[0], cnt = 1;
for (int i = 1; i < a.size(); i++) {
if (res == a[i]) cnt++;
else cnt--;
if (cnt < 0) res = a[i], cnt = 1;
}
return res;
}
众数 K
摩尔投票法(可推广到 k/n):三人肉搏,只有一人活下,在某方团灭后,最少会剩下一支队伍。然后遍历是否满足条件
vector<int> majorityElement(vector<int>& a) {
int n = a.size(), r1, r2, c1 = 0, c2 = 0;
// PK
for (int i = 0; i < n; i++) {
if (c1 && r1 == a[i]) c1++;
else if (c2 && r2 == a[i]) c2++;
else if (!c1) r1 = a[i], c1 = 1;
else if (!c2) r2 = a[i], c2 = 1;
else c1--, c2--;
}
// 统计
c1 = 0, c2 = 0;
for (int i = 0; i < n; i++) {
if (a[i] == r1) c1++;
else if (a[i] == r2) c2++;
}
vector<int> res;
if (c1 > n / 3) res.push_back(r1);
if (c2 > n / 3) res.push_back(r2);
return res;
}
旋转系列
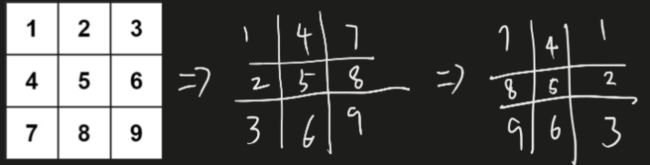
旋转图像
- 先主对角线翻转
- 再按对称轴翻转
void rotate(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
// 主对角线翻转
for (int i = 0; i < n; i++) {
for (int j = i; j < m; j++) {
swap(g[i][j], g[j][i]);
}
}
// 对称轴翻转
for (int i = 0; i < n; i++) {
for (int j = 0; j < m >> 1; j++) {
swap(g[i][j], g[i][m - j - 1]);
}
}
}
旋转数组
这道题是循环右移,408 考过一道循环左移
0 ~ n - 1逆序0 ~ k - 1逆序k ~ n - 1逆序
void rotate(vector<int>& a, int k) {
int n = a.size();
k %= n;
rev(a, 0, n - 1);
rev(a, 0, k - 1);
rev(a, k, n - 1);
}
void rev(vector<int>& a, int l, int r) {
while (l < r) swap(a[l++], a[r--]);
}
左旋字符串
这道题是循环左移,408 真题
0 ~ k - 1逆序k ~ n - 1逆序0 ~ n - 1逆序
string reverseLeftWords(string s, int k) {
int n = s.size();
k %= n;
rev(s, 0, k - 1);
rev(s, k, n - 1);
rev(s, 0, n - 1);
return s;
}
void rev(string& s, int l, int r) {
while (l < r) swap(s[l++], s[r--]);
}
前后缀分解
除自身以外数组的乘积
前后缀分解
生成除自身以外数组乘积的前缀和后缀数组
当前除自身以外数组乘积等于前缀乘后缀
vector<int> multiply(const vector<int>& a) {
int n = a.size();
vector<int> p(n, 1);
for (int i = 1; i < n; i++) {
p[i] = p[i - 1] * a[i - 1]; // 求前缀
}
for (int i = n - 1, s = 1; i >= 0; i--) {
p[i] *= s; // 求除自身以外数组乘积
s *= a[i]; // 求后缀
}
return p;
}
差分与前缀和
区域和检索 - 数组不可变
一维前缀和
class NumArray {
private:
vector<int> p;
public:
NumArray(vector<int>& a) {
int n = a.size();
p.resize(n + 1);
for (int i = 0, x = 0; i < n; i++) {
p[i + 1] = p[i] + a[i];
}
}
int sumRange(int l, int r) {
return p[r + 1] - p[l];
}
};
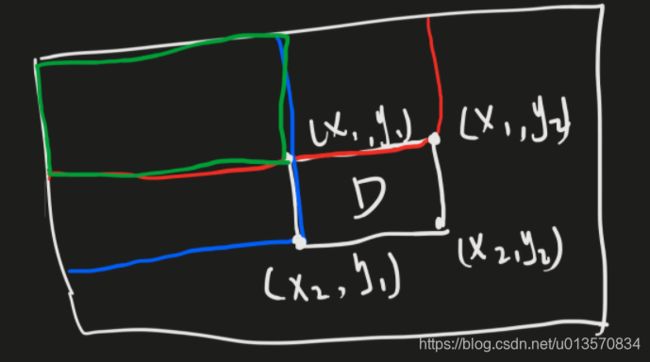
二维区域和检索 - 矩阵不可变
二维前缀和
前缀和数组 s[i][j] = s[i - 1][j] + s[i, j - 1] - s[i - 1][j - 1] + a[i][j]
区域 D 总和 = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1][y1]
class NumMatrix {
private:
vector<vector<int>> s;
public:
NumMatrix(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
s = vector<vector<int>> (n + 1, vector<int> (m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + g[i - 1][j - 1]; // 前缀和数组 1 开始,矩阵数组 0 开始,补上偏移量
}
}
}
int sumRegion(int x1, int y1, int x2, int y2) {
x1++, y1++, x2++, y2++; // 补上偏移量
return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]; // 补上偏移量
}
};
等差数列划分
等差数列性质,相邻元素差相等。所以可用差分数组来做
// 原数组 [1, 2, 3, 4]
// 差分 [1, 1, 1, 1]
// 差分数组元素 1 ~ 3 相等 -> 原数组 0 ~ 3 等差。长度记为 k
// 子数组 [1, 2, 3] [2, 3, 4] [1, 2, 3, 4]
// 子数组个数 k * (k - 1) / 2
int numberOfArithmeticSlices(vector<int>& a) {
int n = a.size(), res = 0;
// 生成差分数组
for (int i = n - 1; i > 0; i--) a[i] -= a[i - 1];
// 统计区间
for (int i = 1; i < n; i++) {
int j = i;
while (j < n && a[i] == a[j]) j++;
int k = j - i;
res += k * (k - 1) / 2;
i = j - 1;
}
return res;
}
内卷法
数组中重复的数据
元素取值范围 1 ~ n ,意味着数组足够标记所有元素的出现次数
有些元素出现两次而其他元素出现一次,可以取反标记已经出现过的元素。如果从负数变为正数则说明元素出现两次
vector<int> findDuplicates(vector<int>& a) {
vector<int> res;
for (auto x : a) {
int p = abs(x) - 1;
a[p] *= -1;
if (a[p] > 0) res.push_back(abs(x));
}
return res;
}
找到所有数组中消失的数字
元素取值范围 1 ~ n ,意味着数组足够标记所有元素的出现次数
a[i] 出现过则在 a[a[i]] 取反标记,标记完后,从头遍历所有元素,没被标记的位置就是没有出现的数字
vector<int> findDisappearedNumbers(vector<int>& a) {
for (auto x : a) {
int p = abs(x) - 1;
if(a[p] > 0) a[p] *= -1;
}
vector<int> res;
for (int i = 0; i < a.size(); i++) {
if (a[i] > 0) res.push_back(i + 1);
}
return res;
}
模拟
数组嵌套
想像成图进行模拟,将已遍历过的点打上标记。如果某个点上有标记,则代表这个环已经被遍历过了
int arrayNesting(vector<int>& a) {
int n = a.size();
int res = 0;
for (int i = 0; i < n; i++) {
if (a[i] != -1) {
int k = 0, j = i;
while (a[j] != -1) {
int next = a[j];
a[j] = -1;
j = next;
k++;
}
res = max(k, res);
}
}
return res;
}
重塑矩阵
先将原矩阵展开为一维数组
然后找到原矩阵和一维数组的坐标映射关系
再找到一维数组与目标矩阵的坐标映射关系
最后通过与一维数组的映射关系,建立原矩阵和目标矩阵的映射关系
vector<vector<int>> matrixReshape(vector<vector<int>>& g, int r, int c) {
int n = g.size(), m = g[0].size();
if (n * m != r * c) return g;
vector<vector<int>> res(r, vector<int>(c));
for (int i = 0; i < n * m; i++) {
res[i / c][i % c] = g[i / m][i % m];
}
return res;
}
去掉最低工资和最高工资后的工资平均值
double average(vector<int>& a) {
int maxv = INT_MIN, minv = INT_MAX;
int n = a.size();
double res = 0;
for (int i = 0; i < n; i++) {
maxv = max(maxv, a[i]), minv = min(minv, a[i]);
res += a[i];
}
res = (res - minv - maxv) / (n - 2);
return res;
}
存在连续三个奇数的数组
bool threeConsecutiveOdds(vector<int>& a) {
int n = a.size();
if (n < 3) return false;
for (int i = 0; i < n - 2; i++) {
if (a[i] & 1 && a[i + 1] & 1 && a[i + 2] & 1) return true;
}
return false;
}
杂七杂八
打乱数组
洗牌算法:第 0 个元素和 1 ~ n-1 中的元素交换;第 1 个元素和 2 ~ n-1 中的元素交换 … 直至第 n - 2 个元素和 n-1 ~ n-1 元素交换
class Solution {
private:
vector<int> a;
int n;
public:
Solution(vector<int>& a) {
this->a = a;
this->n = a.size();
}
/** Resets the array to its original configuration and return it. */
vector<int> reset() {
return a;
}
/** Returns a random shuffling of the array. */
vector<int> shuffle() {
auto b = a;
for (int i = 0; i < n; i++) {
swap(b[i], b[i + rand() % (n - i)]);
}
return b;
}
};