分治算法求解凸包问题

分治算法（Divide and Conquer）是一种解决问题的算法设计策略，它将一个大问题分解成若干个规模较小且相互独立的子问题，然后将这些子问题的解合并起来，从而得到原问题的解。

分治算法通常包括以下三个步骤：

• 分解：将原问题分解为一组子问题，子问题与原问题类似，但是规模更小
• 解决：递归求解子问题，如果子问题足够小，停止递归，直接求解
• 合并：将子问题的解组合成原问题的解

相关概念

• 凸多边形：连接多边形中任意两点的线段全部在多边形内部
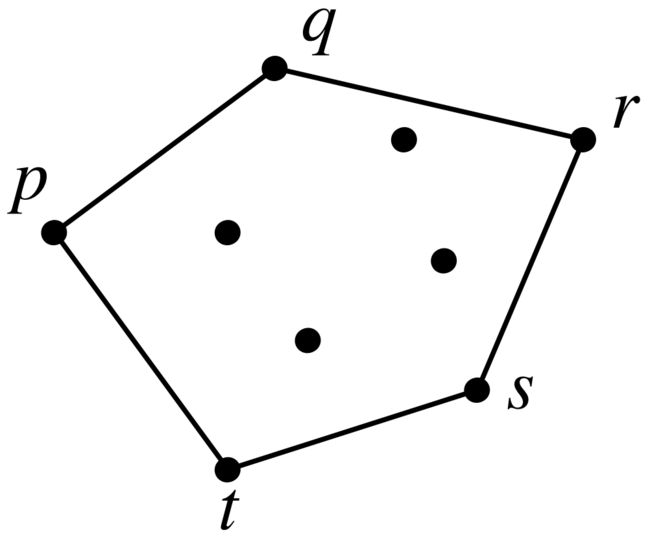
• 平面上某个点集的凸包：包含所有点的最小凸多边形
• 凸包的表示：最小凸多边形的顶点
  1. 集合（无序）
  2. 序列（有序）如上图按顺时针:
• 点和线段的方向关系:
  给定线段$AB$和点$C$，判断$C$与$AB$的位置关系
  计算叉积：$(x_B-x_A,y_B-y_A)\times (x_C-x_B,y_C-y_B)$
  • 大于0： $C$ 在 $AB$ 的左侧
  • 等于0： $C$ 在 $AB$ 所在的直线上
  • 小于0： $C$ 在 $AB$ 的右侧

凸包问题

给定⼆维平面上的n个点集$S=(x_i,y_i)|i=1,2,...,n$ ，找到其凸包

• 假设没有两点具有相同的横坐标
• 假设没有两点具有相同的纵坐标
• 假设没有三点共线

//点结构
struct Point {
    int x, y;
};
//边结构
struct Line {
    Point start, end;
};
//判断点和线段的方向关系
int crossProduct(Point A, Point B, Point C) {
    return (B.x - A.x) * (C.y - B.y) - (B.y - A.y) * (C.x - B.x);
}

1.穷举法求凸包

点穷举

由于凸包是点集S最小的凸多边形的顶点或边，我们可以从几何的角度进行观察，对于每⼀个点，如果它在其他任意三点构成的三角形中，那么它就被凸包所围，换句话说，它不可能是构成最小凸包的点。而那些构成凸包的点则不会处在任意三角形的内部。

根据这个性质，我们可以对点进行穷举：

• 对于每⼀个点，检查其是否在任意其它三点构成的三角形中
• $O(n)$个点， $O(n^3)$个三角形，检查需要$O(1)$时间
• 总的时间复杂度：$O(n^4)$

bool isInsideTriangle(Point A, Point B, Point C, Point P) {
    int crossABP = crossProduct(A, B, P);
    int crossBCP = crossProduct(B, C, P);
    int crossCAP = crossProduct(C, A, P);

    return (crossABP >= 0 && crossBCP >= 0 && crossCAP >= 0) ||
           (crossABP <= 0 && crossBCP <= 0 && crossCAP <= 0);
}

---

边穷举

根据凸包定义，我们也可以通过两个点组成的边来判断其是否属于凸包：

• 属于：所有其它的点都在该线段的⼀侧
• $O(n^2)$条线段，测试需要$O(n)$时间
• 总的时间复杂度：$O(n^3)$
  

bool isConvexHullEdge(vector<Point>& points, Line edge) {
	//遍历点
    for (Point p : points) {
        if (p != edge.start && p != edge.end) {
            int crossProductValue = crossProduct(edge.start, edge.end, p);
            if (crossProductValue > 0) {
                return false;
            }
        }
    }
    return true;
}

---

2.分治法求凸包

对于点集的分解目前有两种分解策略：

• 1/n-1分：分为An-1个点和B1个点
• 二等分：分为A/B两个大小相等的点集

我们先考虑第一种情况，即1/n-1分治

插入凸包

• 分解:把n个点分成A、B两部分，其中A有n -1个点，B只有1个点
  1. 选取一个特别的点q放入B: 最右边的点 (横坐标最大的点)
  2. 该点一定属于新的凸包
• 递归求解A的凸包CH(A)
  • 基本情况: 三个点，直接计算
• 合并CH(A) 和 q
• 算法时间复杂度: $T(n)=T(n-1)+T_{merge}$
  • $T_{merge}=O(n^2)\Rightarrow T(n)=O(n^3)$
  • $T_{merge}=O(n)\Rightarrow T(n)=O(n^2)$
  • $T_{merge}=O(\log n)\Rightarrow T(n)=O(n\log n)$

可以看到，降低插入凸包的复杂度关键是降低Merge时的复杂度。

• 凸包的支撑线: 与凸包仅相交于一点的直线
• 过凸包外一点有且仅有两条该凸包的支撑线 ($q{p}_3$和$q{p}_5$)
• 两个交点 ($p_3$和$p_5$)将凸包边界分成两个链: 近链和远链
• 新的凸包由远链和点q决定
  • 从左支撑线开始，在凸包边界上顺时针前进直到右支撑线

如何求左右支撑线:

暴力求解：

• $O(n)$条候选支撑线$q{p}_i$;
• 检查所有其他点是否在$q{p}_i$同一侧: $O(n)$时间
• 共需$O(n^2)$时间

优化搜索测略：

• 寻找左支撑线
  • 从距离$q$最近的$p_i$开始，检查$p_{(i-1)\%n}$和$p_{(i+1)\%n}$是否都在$q{p}_i$右侧
• 右侧寻找右支撑线
  • 从距离$q$最近的$p_i$开始，检查$p_{(i-1)\%n}$和$p_{(i+1)\%n}$是否都在$q{p}_i$左侧
• $T(n)=T(n-1)+O(n)\Rightarrow T(n)=O(n^2)$

function ConvexHull(S):
    if |S| <= 3:
        return ComputeConvexHull(S)
    else:
        Divide S into A and B
        q = rightmost point in B
        CH_A = ConvexHull(A)
        Merge CH_A with q to form the new convex hull CH

function Merge(CH_A, q):
    Find left and right support lines for CH_A and q
    Traverse the boundary of CH_A from left support line to right support line and update CH

function ComputeConvexHull(S):
    // Implement a convex hull algorithm for small inputs (e.g., Gift Wrapping)

// Initial call to ConvexHull with the entire set of points S
ConvexHull(S)

---

并归凸包

• 分解: 把n个点分成A、B两部分，其中A、B各有n/2个点
• 预处理: 将所有点按横坐标排序
• 递归求解A和B的凸包，记为P和O
  • 基本情况:是不是三个点?
• 合并P和Q
• 算法时间复杂度: $T(n)=2T(n/2)+T_{merge}$
  IF $T_{merge}=O(n)\Rightarrow T(n)=O(nlogn)$

合并过程设计

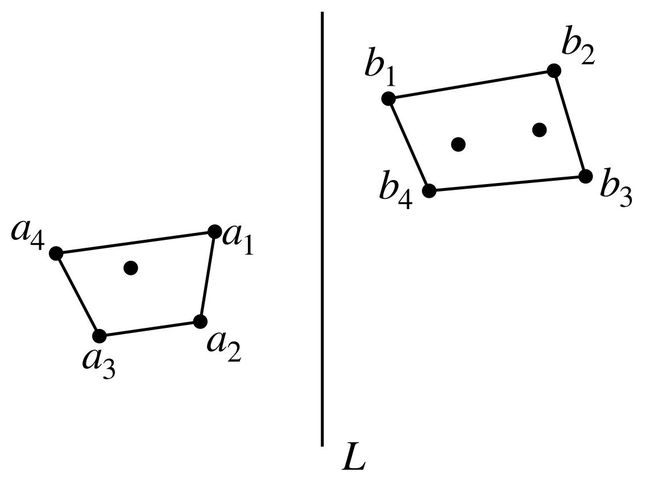
• 凸包P和Q的桥: 既是P的支撑线，也是Q的支撑线 (比如$a_4{b}_1$,和$a_2{b}_1$)
  • 上桥: 如果P和O都在桥的下方
  • 下桥: 如果P和O都在桥的上方
• 找到P和O的上桥和下桥
  • 每个凸包边界被其与桥的交点分成左链和右链
• 合并后的凸包=上桥 + P的左链 + 下桥 + O的右链

寻找上下桥

• 令$a_i$是P中距离L最近的点，$b_j$是Q中距离L最近的点
• 如果$a_i{b}_j$不是$a_i$的左支撑线，找到$a_i$的左支撑线$a_i{b}_j$
  • 顺时针检查$b_j$的下一个点
• 如果$a_i{b}_j$不是$b_j$的右支撑线，找到$b_j$的右支撑线$a_i{b}_j$
  • 逆时针检查$a_i$的下一个点
• 重复上述步骤直到$a_i{b}_j$既是$a_i$的左支撑线，又是$b_j$的右支撑线，即为上桥
• 下桥类似求解
• 寻找上桥和下桥时间复杂度: O(n)
• 合并时间复杂度: O(n):
  $T(n)=2T(n/2)+O(n)\Rightarrow T(n)=O(nlogn)$

---

快速凸包

• 按照x轴排序后选择最大和最小两个极端点a和b (一定属于凸包)
• $ab$将整个点集分成两部分: $ab$左边的点集A、$ab$右边的点集B

1. A中哪些点一定属于凸包?

• 距离 $ab$ 最远的点c: O(1)时间可确定c到$ab$的距离
• $△abc$ 中的点一定不属于凸包
• $△abc$ 外的点?
  • $bc$右边的点: 递归求解哪些点属于凸包
  • $ca$右边的点: 递归求解哪些点属于凸包

2. B中哪些点一定属于凸包?

quick_hull($S$) :
$(a,b)$ ← extreme_points($S$)
$A$ ← right_of $(S,ba)$
$B$ ← right_of $(S,ab)$
$Q_A$ ← quick_half_hull$(A,ba)$
$Q_B$ ← quick_half_hull$(A,ab)$
return $\{a\}\cup Q_A\cup \{b\}\cup Q_B$

quick_half_hull$(S,ba)$:
if $(s=\oslash )$ return $\oslash$
c ← furthest$(S,ba)$
A ← right_of$(S,bc)$
B ← right_of$(S,ca)$
$Q_A$ ← quick_half_hull$(S,bc)$
$Q_B$ ← quick_half_hull$(S,ca)$
return $Q_A\cup \{c\}\cup Q_B$

时间复杂度分析
令 $|S|=n，|A|=\alpha ,|B|=\beta ,\alpha +\beta \le n-1$

• quick_half_hull
  • $T(n)=T(\alpha )+T(\beta )+O(n)$
    1.$\alpha =\beta =\frac{n}{2}\Rightarrow T(n)=O(nlogn)$
    2.$\alpha =0,\beta =n-1\Rightarrow T(n)=O(n^2)$
• quick_hull
  • 预排序计算极端点：$O(nlogn)$
  • 计算A和B：$O(n)$
  • 递归求解A和B：$<2T(n)$
  • 最坏情况下也是$O(n^2)$

#include 
#include 
using namespace std;

struct Point {
    int x, y;
};
//判断C在AB的哪一侧
int crossProduct(Point A, Point B, Point C) {
    return (B.x - A.x) * (C.y - B.y) - (B.y - A.y) * (C.x - B.x);
}
//计算点C到直线AB的距离
double distanceToLine(Point A, Point B, Point P) {
    int crossProductValue = abs((B.x - A.x) * (A.y - P.y) - (A.x - P.x) * (B.y - A.y));
    double lengthAB = sqrt(pow(B.x - A.x, 2) + pow(B.y - A.y, 2));
    return crossProductValue / lengthAB;
}
//找到两个极端点
vector<Point> findExtremePoints(vector<Point>& S) {
    Point leftmost = S[0], rightmost = S[0];
    for (Point p : S) {
        if (p.x < leftmost.x)
            leftmost = p;
        if (p.x > rightmost.x)
            rightmost = p;
    }
    return {leftmost, rightmost};
}
//计算ab直线的右侧点点集，需要注意的是ab和ba的统计效果相反
vector<Point> rightOf(vector<Point>& S, Point a, Point b) {
    vector<Point> result;
    for (Point p : S) {
        if (crossProduct(a, b, p) < 0)
            result.push_back(p);
    }
    return result;
}
//计算点集最远端点
Point findFurthestPoint(vector<Point>& S, Point a, Point b) {
    Point furthest = S[0];
    int maxDist = -1;
    for (Point p : S) {
        double dist = distanceToLine(a, b, p);
        if (dist > maxDist) {
            maxDist = dist;
            furthest = p;
        }
    }
    return furthest;
}

vector<Point> quickHalfHull(vector<Point>& S, Point a, Point b) {
    if (S.empty())
        return {};

    Point c = findFurthestPoint(S, a, b);
    vector<Point> A = rightOf(S, b, c);
    vector<Point> B = rightOf(S, c, a);
    vector<Point> QA = quickHalfHull(A, b, c);
    vector<Point> QB = quickHalfHull(B, c, a);

    vector<Point> result = QA;
    result.push_back(c);
    result.insert(result.end(), QB.begin(), QB.end());

    return result;
}

vector<Point> quickHull(vector<Point>& S) {
    vector<Point> extremePoints = findExtremePoints(S);
    Point a = extremePoints[0];
    Point b = extremePoints[1];

    vector<Point> A = rightOf(S, b, a);
    vector<Point> B = rightOf(S, a, b);

    vector<Point> QA = quickHalfHull(A, b, a);
    vector<Point> QB = quickHalfHull(B, a, b);

    vector<Point> result = QA;
    result.push_back(a);
    result.insert(result.end(), QB.begin(), QB.end());

    return result;
}

int main() {
    // Example usage
    vector<Point> points = {{0, 0}, {1, 1}, {2, 2}, {3, 3}, {0, 3}};
    vector<Point> convexHull = quickHull(points);

    cout << "Convex Hull Points: ";
    for (Point p : convexHull) {
        cout << "(" << p.x << ", " << p.y << ") ";
    }
    cout << endl;

    return 0;
}