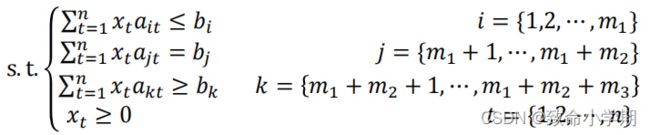【算法设计zxd】第3章迭代法04 线性规划

线性规划 研究 线性约束条件 下 线性目标函数 的极值问题 的数学理论和方法。

线性规划问题形式 化表达

目标函数

 约束条件

线性规划问题的可行性解

线性规划问题的 可行区域

线性规划问题的 最优解（x 1 ,x 2 ,…… ， x n 的值）

线性规划问题的 最优值

 单纯形算法特点

(1) 只对约束条件的若干组合进行测试，测试的毎一步都使 目标函数的值向期望值逼近；

(2) 一般经过不大于 m 或 n 次迭代就可求得最优解。

线性规划标准形式

(1)它必须是一个最大化问题。如果是最小化问题，只需要把 目标函数的所有系统 c j 替换为 -c j 即可， j=1,2,…,n ；

(2)所有的约束都必须用线性方程的形式表示（除了非负约束， 即 x t ≥0 ）；

(3) 所有的变量都必须是非负的。

基本变量：每个等式约束中至少有一个变量的系数为正， 且这个变量只在该约束中出现。在每一约束方程中选择一 个这样的变量，并以它作为变量求解该约束方程 (m 个 ) 。

非基本变量： 余下 n-m 个变量

【例3-9】设有下列形式的线性规划问题，求max z。

目标函数         max z =-x2 +3x 3 -2x 5

约束条件s.t.     x1 +3x 2 -x 3 +2x 5 =7

                        x4-2x2 +4x 3 =12

                        x6-4x2 +3x 3 +8x 5 =10

                        xi≥0 (i=1,2,3,4,5,6)

 问题分析

依题意可知， n=6, m=3

基本变量为： x l ， x 4 ， x 6

非基本变量： x 2 ， x 3 ， x 5

基本可行解： x=(7, 0, 0, 12, 0, 10)

步骤 1 ：选出使目标函数增加的非基本变量作为入基变量 (x 3 )

步骤 2 ：选出离基变量，因为 min{12/4,10/3}=3 ，所以选 x 4

步骤 3 ：转轴变换。转轴变换的目的是将入基变量与离基变量互调位置。



计算模型

i代表行，j代表列，e入基变量所在的列，k是离基变量所 在的行。 新基本变量下标B’=B+{e}

-{k}，新非基本变量下标 N’=N+{k}-{e}。

步骤1：选入基变量。

如果所有cj≤0，则当前基本可行解为最 优解，计算结束。否则，取ce>0，相应的非基本变量 x

e为入 基变量。



计算模型

i代表行，j代表列，e入基变量所在的列，k是离基变量所 在的行。

新基本变量下标B’=B+{e}-{k}，新非基本变量下标 N’=N+{k}-{e} 。

步骤1：选入基变量。

如果所有cj≤0，则当前基本可行解为最 优解，计算结束。否则，取

ce>0，相应的非基本变量xe为入 基变量。

步骤2：选离基变量。

对于入基变量xe，如果所有 a_ie≤0(i=1,2, …, m)，则最优解无界，计算结束。否则，计算

选取基本变量xk为离变量。

步骤3：转轴变换。

 

一般线性规划问题的单纯形法:

引入松弛变量，利用松弛变量的非负性将不等式转化为等式，在求解过

程中，将松弛变量与原来变量 x i 同样对待，在求解结束后，抛弃松弛变量。

引入松弛变量后，可能不是在所有的约束方程中都能找到基本变量，还需要

引入 m 个人工变量 z i （包括约束条件中的等式），进一步构造标准型约束。

 【例3-10】目标函数 max z = x1+x2+3x3-x4

s.t.

x 1 +2x 3 ≤18

2x 2 -7x 4 ≤0

x 1 +x 2 +x 3 +x 4 =9

x 2 -x 3 +2x 4 ≥1

x i ≥1 i=1,2,3,4

解：引入松弛变量 y i , 得

x 1 +2x 3 + y 1 =18

2x 2 -7x 4 + y 2 = 0 (1)

x 1 +x 2 +x 3 +x 4 =9

x 2 -x 3 +2x 4 - y 3 = 1

引入 z i , 得

z 1 +x 1 +2x 3 + y 1 =18

z 2 +2x 2 -7x 4 + y 2 = 0 (2)

z 3 +x 1 +x 2 +x 3 +x 4 =9

z 4 +x 2 -x 3 +2x 4 - y 3 = 1

引入 z i 使得 (1) 和 (2) 并不等价，为了解决这个问题，在求解时必须分两个阶段进行

第 2 阶段利用第 1 阶段的初始基本可行性解，

运用单纯形法求解由 (1) 中约束条件约束的标

准形式的纯属规划问题，此时，使用原问题

的目标函数。

第 1 阶段第 1 阶段用一个辅助目标函数替代原来的目标函数，同时把 (2) 中的 s.t. 代

入这个目标函数中，得：

z’=-z 1 -z 2 -z 3 -z 4 =-(28-2x 1 -4x 2 -2x 3 +4x 4 -y 1 -y 2 +y 3 )

新构造的线性规划问题称为原线性规划问题的 辅助线性规划问题 。用单纯形法

对新辅助线性规划问题进行求解。如果原问题有可行性解，则辅助线性规划问

题就有最优解，且其最优值为 0 ，即所有 z i 都为 0 。在辅助线性规划问题最后的单

纯形表中，所有 z i 均为非基本变量。去掉所有 z i 相应的列，乘下的就是只含有 x i 和

y i 的标准形式的线性规划问题。那么，第 1 阶段的主要任务就是构造一个初始基

本可行性解。

注意：

（ 1 ） 如果在辅助线性规划问题最后的单纯形表中， z i 不全 为 0 ，则原线性规划问题没有可行性解，从而原线性规划问 题无解。

（ 2 ）用单纯形算法解一般的线性规划问题时，可能会遇到 退化情形，即在迭代计算的某一步中，常数列中的某个元 素的值变成 0 ，使得相应的基本变量取值为 0 。如果选取退 化的基本变量为离基变量，则作转轴变换前后的目标函数 值不变。在这种情况下，算法不能保证目标函数值严格递

增，因此可能出现循环。

思考题：

仓库租凭问题 某企业计划为流通的货物租赁若干

批仓库。要求：必须保证在时间段 i=1,2,…,n ，有 b i 的仓

库容量可用。现在若干仓库源可供选择。设 c ij 是从时间

段 i 到时间段 j 租用 1 个单侠仓库容量的价格， 1≤i≤j≤n 。

问题是：应如何安排仓库租赁计划才能满足各时间段

的仓库需求，且使租赁费用最少