相关样本t检验之验证特鲁普效应
项目背景和目的
斯特鲁普效应(Stroop effect)在心理学中指优势反应对非优势反应的干扰。例如当测试者被要求回答有颜色意义的字体的颜色时,回答字本身的意义为优势反应,而回答字体颜色为非优势反应,若字体颜色与字意不同,被测者往往会反应速度下降,出错率上升。
实验目的:验证斯特鲁普效应
一、描述统计分析
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 准备数据
data=pd.read_csv(r'C:\Users\EDY\Desktop\吧哩吧啦\学习\Untitled Folder\斯特鲁普数据集.csv')
data.head()
| Congruent | Incongruent | |
|---|---|---|
| 0 | 12.079 | 19.278 |
| 1 | 16.791 | 18.741 |
| 2 | 9.564 | 21.214 |
| 3 | 8.630 | 15.687 |
| 4 | 14.669 | 22.803 |
理解数据
Congruent为颜色和字意一致时实验者的反应时间
Incongruent为颜色和字意不一致时实验者的反应时间
# 查看描述统计信息
data.describe()
| Congruent | Incongruent | |
|---|---|---|
| count | 24.000000 | 24.000000 |
| mean | 13.926875 | 22.350750 |
| std | 3.540219 | 5.010218 |
| min | 8.630000 | 15.687000 |
| 25% | 11.895250 | 18.716750 |
| 50% | 13.627500 | 21.046000 |
| 75% | 15.671250 | 24.536000 |
| max | 22.328000 | 35.255000 |
# 第一组数据均值
sample1_mean=data['Congruent'].mean()
# 第一组数据标准差
sample1_std=data['Congruent'].std()
# 第二组数据均值
sample2_mean=data['Incongruent'].mean()
# 第二组数据标准差
sample2_std=data['Incongruent'].std()
# 画图比较2组数据的不同
fig=plt.figure(figsize=(20,10))
ax=fig.add_subplot(1,1,1)
data.plot(kind='bar',ax=ax)
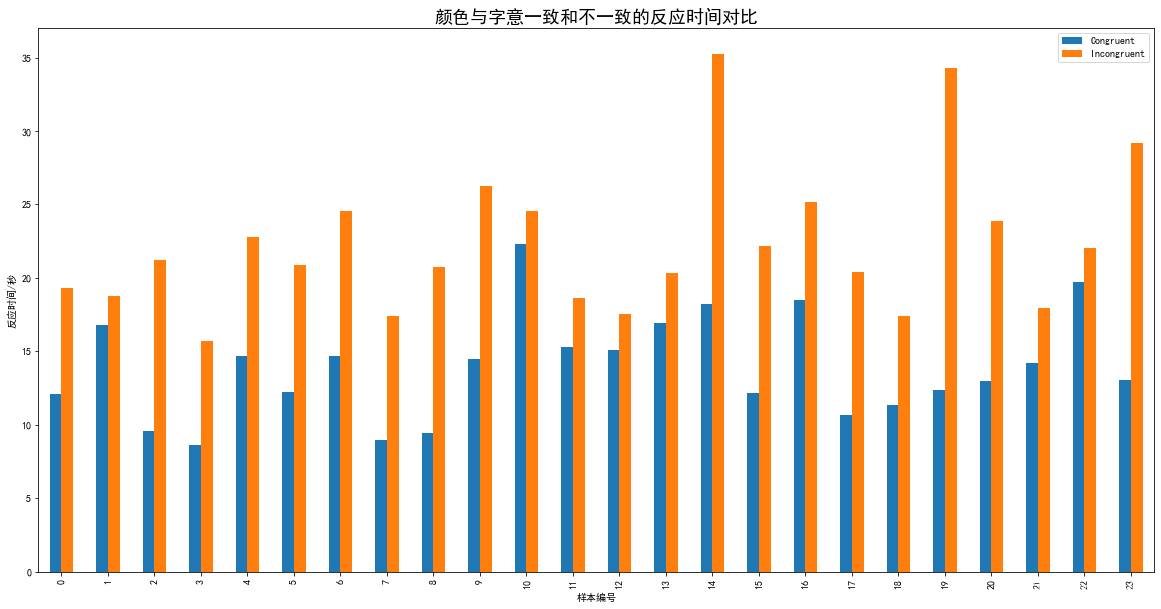
plt.title('颜色与字意一致和不一致的反应时间对比',fontsize=18)
plt.xlabel('样本编号')
plt.ylabel('反应时间/秒')
plt.show()
print('第一组样本量大小%d,样本平均值%.2fs,样本标准差%.2fs'%(24,sample1_mean,sample1_std))
print('第二组样本量大小%d,样本平均值%.2fs,样本标准差%.2fs'%(24,sample2_mean,sample2_std))
print('观察柱状图,当颜色与字意不一致时,实验者普遍反应时间偏长')
第一组样本量大小24,样本平均值13.93s,样本标准差3.54s
第二组样本量大小24,样本平均值22.35s,样本标准差5.01s
观察柱状图,当颜色与字意不一致时,实验者普遍反应时间偏长
二、推论统计分析
(一)假设检验
1、提出假设
自变量为颜色和字意是否相同
因变量为实验者的反应时间
零假设H0:人的反应时间同颜色和字意是否相同无关即μ1=μ2
备择假设:人的反应时间同颜色和字意是否相同有关,当颜色和字意不同时,人的反应时间变长,即特鲁普效应确实存在,μ1<μ2
2、检验类型
两组数据是相关样本,所以选择相关配对检验。
配对t检验配对定量数据之间的差异对比关系。处理方法为将观测值转换为差值,对其差值进行单样本t检验
# 增加差值列,简历差值数据集
data['Diff']=data['Congruent']-data['Incongruent']
data.head()
| Congruent | Incongruent | Diff | |
|---|---|---|---|
| 0 | 12.079 | 19.278 | -7.199 |
| 1 | 16.791 | 18.741 | -1.950 |
| 2 | 9.564 | 21.214 | -11.650 |
| 3 | 8.630 | 15.687 | -7.057 |
| 4 | 14.669 | 22.803 | -8.134 |
3、抽样分布类类型
样本数t=24,小于30,属于小样本。进一步查看其分布是否近似于正态分布
sns.displot(data['Diff'],kde=True)
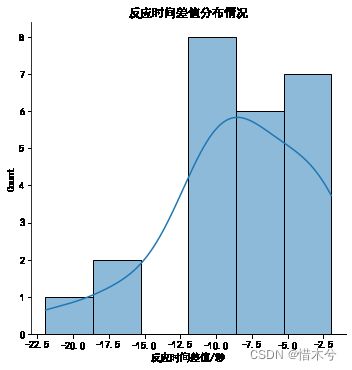
plt.title('反应时间差值分布情况')
plt.xlabel('反应时间差值/秒')
plt.show()
观察反应时间差值分布图,可以看出其差值近似于正态分布,差值符合单样本t检验
4、检测方向
备择假设要验证μ1是否小于μ2,即验证差值是否小于0,属于左侧检验
5、置信水平
# 置信水平采用95%
alpha=0.05
6、P值
from scipy import stats
t,p_two=stats.ttest_rel(data['Congruent'],data['Incongruent'])
print('t(%d)=%.2f,p=%.10f(α=0.05),相关配对t检验(左侧)'%(24,t,p_two/2))
t(24)=-8.09,p=0.0000000177(α=0.05),相关配对t检验(左侧)
7、结论
p值远远小于alpha,拒绝H0,说明特鲁普效应确实存在。
(二)置信区间
# 差值样本数n=24,alpha=0.05,one-tailed 查表得t值
t_ci=2.064
n=24
# 差值平均值
sampleDiff_mean=data['Diff'].mean()
#标准误差
se=stats.sem(data['Diff'])
# 置信区间上限
a=sampleDiff_mean-t_ci*se
# 置信区间下限
b=sampleDiff_mean+t_ci*se
print('反应时间差值的置信区间,95%%置信水平CI=(%.2f,%.2f)'%(a,b))
反应时间差值的置信区间,95%置信水平CI=(-10.57,-6.27)
(三)效应量
# 差值标准差
sampleDiff_std=data['Diff'].std()
d=(sampleDiff_mean-0)/sampleDiff_std
d
-1.6510807805255567
三、总结
1、描述统计分析
第一组样本量大小24,样本平均值13.93s,样本标准差3.54s
第二组样本量大小24,样本平均值22.35s,样本标准差5.01s
2、推论统计分析
1)假设检验
t(24)=-8.09,p=0.0000000177(α=0.05),相关配对t检验(左侧)
P值远远小于α,拒绝H0,说明特鲁普效应确实存在。
2)置信区间
反应时间差值的置信区间,95%置信水平CI=(-10.57,-6.27)
说明颜色和字意不一致的反应时间比颜色和字意一致的反应时间平均要多6.27-10.57秒。
3)效应量
d=-1.65,效果显著