Leetcode Hot100不熟练题目 32. 最长有效括号

1、题目描述

给你一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。
示例 1：

输入：s = “(()”
输出：2
解释：最长有效括号子串是 “()”
示例 2：

输入：s = “)()())”
输出：4
解释：最长有效括号子串是 “()()”
示例 3：

输入：s = “”
输出：0

提示：

0 <= s.length <= 3 * 10^4
s[i] 为 ‘(’ 或 ‘)’

2、思路及代码

1、暴力

由于最长有效括号一定是偶数，所以按照最大的偶数区间寻找有效括号，当寻找到的时候，当前的区间长度就是答案。
例如 字符串长度为6，我们最开始找0-5是否全是有效括号。如果不是我们就把区间长度改成4，找0-3，1-4，2-5这些区间是否是有效的。如果有一个是，则答案就是4。否则就把区间长度改成2。

class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size() - s.size() % 2;
        //i代表区间长度
        for(int i = n; i > 0; i -= 2)
        {
        	//j代表开始位置
            for(int j = 0; j + i <= s.size(); j ++)
            {
            	//判断从j 到 j + i - 1之间的括号数组是否是合法的
                int l = 0, r = 0;
                bool isbreak = false;
                for(int k = j; k < j + i; k ++)
                {
                    if(s[k] == '(') l ++;
                    else r ++;
                    //	当发现不合法就break
                    if(l < r) { isbreak = true; break; }
                }
                // 如果是合法的就返回当前区间
                if(l == r && !isbreak) return i;
            }
        }
        return 0;
    }
};

时间复杂度$O(n^3)$,超时

2、动态规划

设f[i]代表以s[i]结尾的最长合法括号长度。那么现在来推导递推公式。
首先我们知道，合法括号都是以）结尾的，以（结尾的f[i]一定是0。
我们在看如何计算以）结尾的f[i],以）为结尾的f[i]计算可以分成两部分考虑。
当s[i - 1] = ')‘和s[i - 1] 为 ‘(’

当s[i - 1] == '(‘时，首先f[i] = f[i - 2] + 2，然后还要加上以s[i - 1- 1]为结尾的最长合法括号的长度。也就是f[i] = f[i - 1] + 2 + f[i - 2]

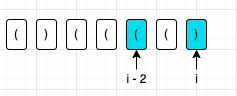
当s[i -1] == ‘)’,情况比较复杂

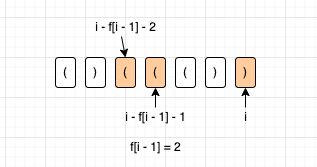
首先我们得看看“前面”有没有和）配对的。这个前面就是指以s[i - 1]结尾的这个最长合法括号之前的位置有没有和）配对的（。如果有那么f[i] 的长度目前就是f[i - 1] + 2。还有一点需要考虑，那就是以s[i - f[i - 1] -2]结尾的合法串长度，也需要加进来。所以在有配对的情况下，f[i] = f[i - 1] + 2 + f[i - f[ i - 1] - 2]。在没有配对的情况下，当前以s[i]结尾的合法字符串长度就是0。
最后再把f中的最大值计算出来即可。

class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size();
        vector<int> f(n + 3,0);
        //为了避免后面i - 2 \ i - f[i - 1] - 1之类的越界，加上点。直接判断也行
        s = "  " + s;
        for(int i = 2; i <= n + 1; i ++)
        {
            if(s[i] == '(') continue;
            if(s[i - 1] == '(')  f[i] = f[i - 1] + 2 + f[i - 2];
            else if(s[i - 1] == ')' && s[i - f[i - 1] - 1] == '(') f[i] = 2 + f[i - 1] + f[i - f[i - 1] - 2];
        }
        int ans = 0;
        for(int i = 2; i <= n + 1; i ++)
        {
            ans = max(ans, f[i]);
        }
        return ans;
    }
};

时间复杂度$O(n)$,空间复杂度$O(n)$

3、栈

使用栈也是我们处理括号匹配问题经常用的方法。当s[i] = (时，直接入栈其坐标i，遇到）先弹栈，此时如果栈为空，则证明无法组成合法括号。此时将当前的i入栈，代表下一个合法括号只能从i + 1开始。如果不为空，假设栈顶元素为k，那么此时表示从k + 1（也就是栈顶的下一个元素） 到i之间的所有括号为合法的。

class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> st;
        //现在栈为空，我们要把-1入栈，表示下一个合法括号只能从0开始。
        st.push(-1);
        int ans = 0;
        for(int i = 0; i < s.size(); i ++)
        {
        	//左边括号，直接入栈
            if(s[i] == '(') st.push(i);
            else {
                st.pop();
                if(st.empty()) st.push(i);
                else ans = max(ans, i - st.top());
            }
        }
        return ans;
    }
};

4、扫两遍

扫两遍的思路好像是最简单的。唯一的问题是为什么要扫两遍。
从左到右遍历字符串s，遇到做括号，lnum ++, 遇到右括号 rnum ++。当lnum == rnum 的时候，更新下最大值。当lnum < rnum 的时候，代表有了非法的括号组合，之前积累的lnum和rnum清零。
这个方法的 问题是，只有在lnum == rnum的时候才会更新答案，遇到像这样的情况(()的时候，()的长度不会被更新答案。所以这个时候，我们只要从右往左重新扫一遍就可以了，因为从右往左的时候（）是会被更新答案的。

class Solution {
public:
    int longestValidParentheses(string s) {
        int lnum = 0, rnum = 0,ans = 0;
        int n = s.size();
        for(int i = 0; i < n; i ++)
        {
            if(s[i] == '(') lnum ++;
            else rnum ++;

            if(lnum < rnum) lnum = 0, rnum = 0;
            else if(lnum == rnum) ans = max(ans,lnum + rnum);
        }

        lnum = 0, rnum = 0;
        for(int i = n - 1; i >= 0; i --)
        {
            if(s[i] == ')') rnum ++;
            else lnum ++;
            //注意反过来扫描条件要颠倒一下
            if(lnum > rnum) lnum = 0, rnum = 0;
            else if(lnum == rnum) ans = max(ans,lnum + rnum);
        }
        return ans;
    }
};