Kruskal(克鲁斯卡尔)算法(图+代码+例题)
Kruskal(克鲁斯卡尔)算法
Kruskal算法是求解 最小生成树 的经典算法之一
0.准备工作
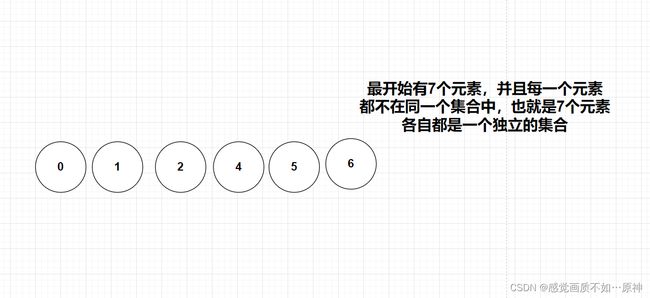
在学习 Kruskal算法 之前,需要先学习一种数据结构-并查集(Disjoint-set data structure),它可以快速的将两个不相交的集合合并,也可以查询两个元素是否在同一个集合当中
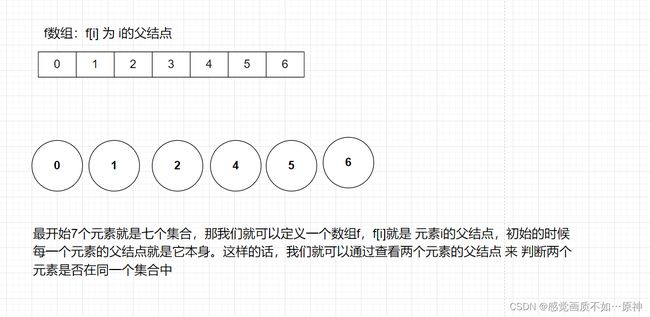
1.并查集的基本思想
2.代码实现
//初始化,有 0 ~ n-1 共n个元素
void init(){
for(int i = 0;i < n;i++) f[i] = i;
}
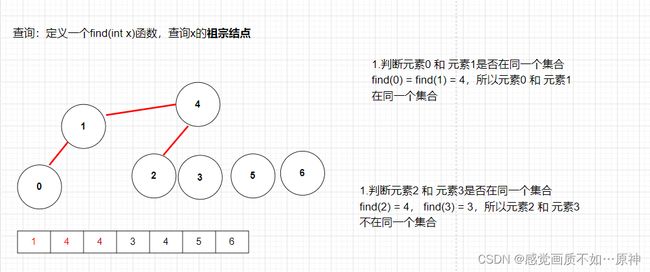
//递归查找祖宗结点
int find(int x){
//只有当 一个结点的父结点 等于 它本身,才找到了祖宗节点
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
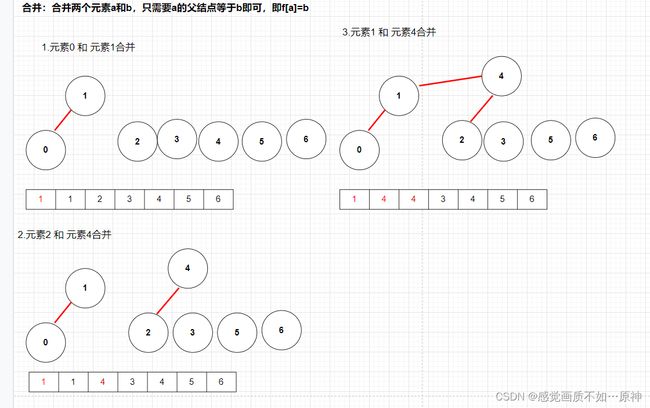
// 合并
void merge(int a,int b){
//如果已经是在同一个集合就不用合并了
if(find(a) != find(b))
f[find(a)] = find(b);
}
1.Kruskal算法的基本思想
首先先定义一个结构存储所有的边 e d g e edge edge ( f r o m , t o , w e i g h t ( 权值 ) ) (from,to,weight(权值)) (from,to,weight(权值)),然后再按权值从小到大的排序,这样我们从头开始遍历,每一次取出来的边都是权值最小的一条边。每次先判断取出的边的两点是否已经在一个集合中了,不在一个集合中就合并,记录权值,反之就跳过本次循环。循环结束,我们就将所有的结点都加到了一个集合中。
-
取出第一条边,集合中的元素为 { { 1 } , { 2 } , { 3 } , { 4 } , { 5 , 6 } , { 7 } } \{\{1\},\{2\},\{3\},\{4\},\{5,6\},\{7\}\} {{1},{2},{3},{4},{5,6},{7}}
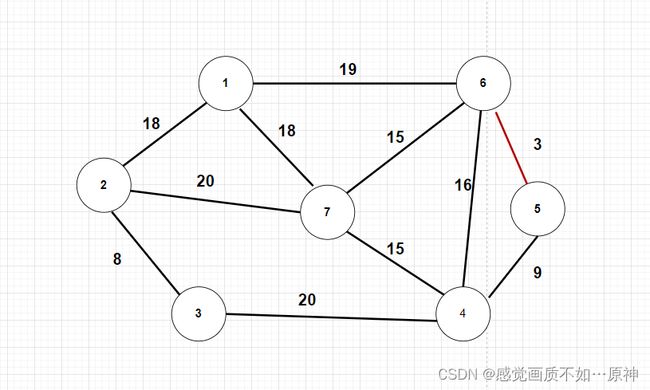
-
取出第二条边,集合中的元素为 { { 1 } , { 2 , 3 } , { 4 } , { 5 , 6 } , { 7 } } \{\{1\},\{2,3\},\{4\},\{5,6\},\{7\}\} {{1},{2,3},{4},{5,6},{7}}
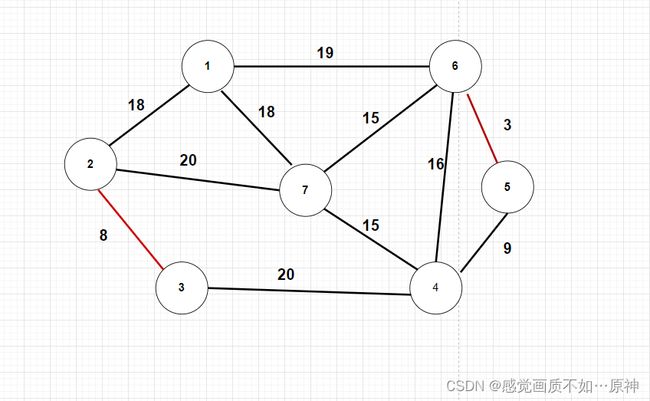
-
取出第三条边,集合中的元素为 { { 1 } , { 2 , 3 } , { 4 , 5 , 6 } , { 7 } } \{\{1\},\{2,3\},\{4 , 5,6\},\{7\}\} {{1},{2,3},{4,5,6},{7}}
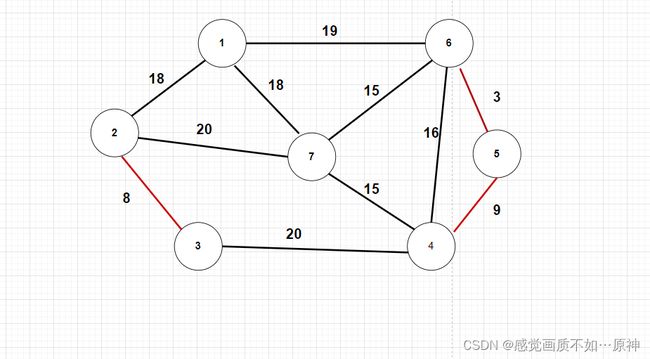
-
取出第四条边,集合中的元素为 { { 1 } , { 2 , 3 } , { 4 , 5 , 6 , 7 } } \{\{1\},\{2,3\},\{4 , 5,6,7\}\} {{1},{2,3},{4,5,6,7}}
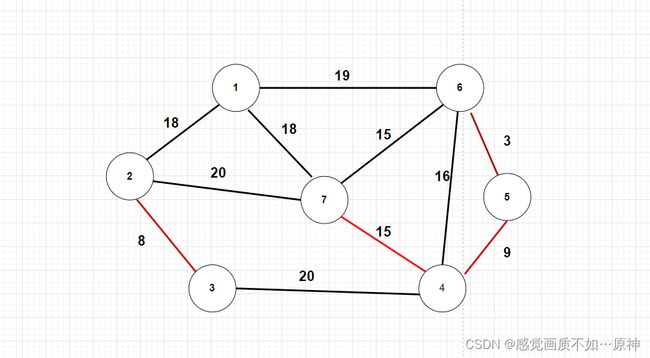
-
取出第五条边,集合中的元素为 { { 1 , 2 , 3 } , { 4 , 5 , 6 , 7 } } \{\{1,2,3\},\{4 , 5,6,7\}\} {{1,2,3},{4,5,6,7}}
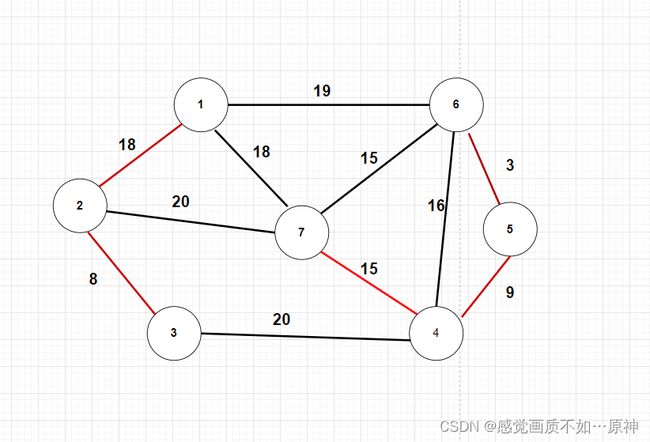
-
取出第六条边,集合中的元素为 { { 1 , 2 , 3 , 4 , 5 , 6 , 7 } } \{\{1,2,3,4 , 5,6,7\}\} {{1,2,3,4,5,6,7}},结束。最小生成树的权重为71。
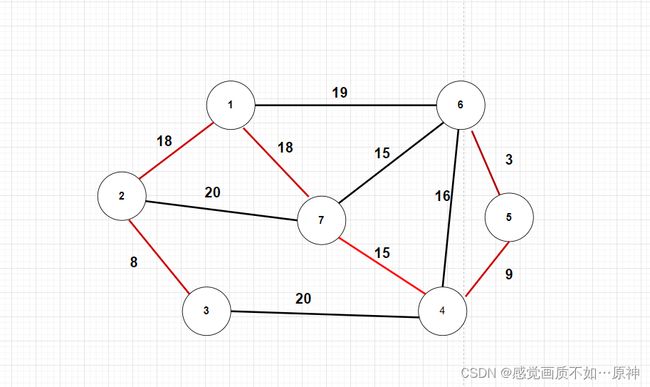
2.代码实现
输入:
7 11
1 2 18
1 6 19
1 7 18
2 7 20
2 3 8
3 4 20
4 7 15
4 6 16
4 5 9
5 6 3
6 7 15
输出:
5 ---> 6 权重为:3
2 ---> 3 权重为:8
4 ---> 5 权重为:9
4 ---> 7 权重为:15
1 ---> 2 权重为:18
1 ---> 7 权重为:18
71
C++代码:
#includeJava代码:
package com.wurusai.graph;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Main {
private static final int N = 100010;
private static final int INF = (int)Math.pow(10,9);
private static int[] f;
private static int n,m;
private static Edge[] edges;
private static int find(int x){
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
private static int kruskal(){
for(int i = 1;i <= n;i++) f[i] = i;
Arrays.sort(edges, new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.w - o2.w;
}
});
int ans = 0,cnt = 0;
for(int i = 0;i < m;i++){
int a = edges[i].a,b = edges[i].b,w = edges[i].w;
int x = find(a),y = find(b);
if(x != y){
f[x] = y;
ans += w;
cnt++;
System.out.println(a + " ---> "+b+" 权值为 "+w);
}
}
if(cnt < n - 1) return INF;
return ans;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入点数和边数:");
n = sc.nextInt();
m = sc.nextInt();
edges = new Edge[m];
f = new int[N];
for(int i = 0;i < m;i++){
int a,b,w;
a = sc.nextInt();
b = sc.nextInt();
w = sc.nextInt();
edges[i] = new Edge(a,b,w);
}
int t = kruskal();
if(t == INF) System.out.println("无法形成最小生成树!!!");
else System.out.println(t);
}
}
class Edge{
public int a,b,w;
public Edge(int a,int b,int w){
this.a = a;
this.b = b;
this.w = w;
}
public Edge(){
}
}
3.例题
题目链接
Kruskal算法求最小生成树
题目描述
给定一个 n n n 个点 m m m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V 表示图中点的集合, E E E 表示图中边的集合, n = ∣ V ∣ n=|V| n=∣V∣, m = ∣ E ∣ m=|E| m=∣E∣。
由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。
输入格式
第一行包含两个整数 n n n 和 m m m。
接下来 m m m 行,每行包含三个整数 u , v , w u,v,w u,v,w,表示节点 u u u 和节点 v v v 之间存在一条权值为 w w w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
- 1 ≤ n ≤ 1 0 5 1≤n≤10^5 1≤n≤105
- 1 ≤ m ≤ 2 ∗ 1 0 5 1≤m≤2∗10^5 1≤m≤2∗105
- 图中涉及边的边权的绝对值均 不超过 1000 1000 1000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
时间复杂度: O ( m × l o g m ) O(m \times logm) O(m×logm)
代码:
#include