python实现模糊洗衣机
- 使用python设计并实现一个洗衣机模糊推理系统实验。
已知人的操作经验是:
污泥越多,油脂越多,洗涤时间越长
污泥适中,油脂适中,洗涤时间适中
污泥越少,油脂越少,洗涤时间越短
洗衣机的模糊控制规则如表1所示:
表1 洗衣机的模糊控制规则表
| 污泥油脂 | NG(无油脂) | MG(中等油脂) | LG(油脂多) |
|---|---|---|---|
| SD(污泥少) | VS | M | L |
| MD(中等污泥) | S | M | L |
| LD(污泥多) | M | L | VL |
其中SD(污泥少)、MD(污泥中)、LD(污泥多)、NG油脂少、MG油脂中、LG油脂多、VS洗涤时间很短、S洗涤时间短、M洗涤时间中等、L洗涤时间长、VL洗涤时间很长。
(1)假设污泥、油脂、洗涤时间的论域分别为[0,100] [0,100] [0,120],设计相应的模糊推理系统,给出输入、输出语言变量的隶属函数图,模糊控制规则表和推论结果立体图。
(2)假定当前传感器测得的信息为污泥=60,油脂=70,采用模糊决策,给出模糊推理结果,并观察模糊推理的动态仿真环境,给出其动态仿真环境图。
import numpy as np
import skfuzzy as fuzz
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
from skfuzzy import control as ctrl
#定义输入输出的取值范围
# 污泥和油脂范围为[0,100]
# 洗涤时间范围为[0,120]
x_stain = np.arange(0, 101, 1)
x_oil = np.arange(0, 101, 1)
x_time = np.arange(0, 121, 1)
# 定义模糊控制变量
stain = ctrl.Antecedent(x_stain, 'stain')
oil = ctrl.Antecedent(x_oil, 'oil')
time = ctrl.Consequent(x_time, 'time')
# 生成模糊隶属函数
#函数中的三元变量,第一个代表折线的起点,第二是最大值,第三是终点
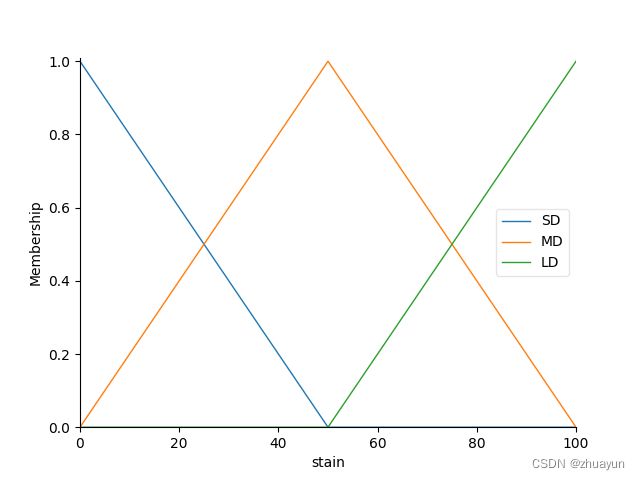
stain['SD'] = fuzz.trimf(x_stain, [0, 0, 50]) #定义污渍的三角隶属度函数横坐标
stain['MD'] = fuzz.trimf(x_stain, [0, 50, 100])
stain['LD'] = fuzz.trimf(x_stain, [50, 100, 100])
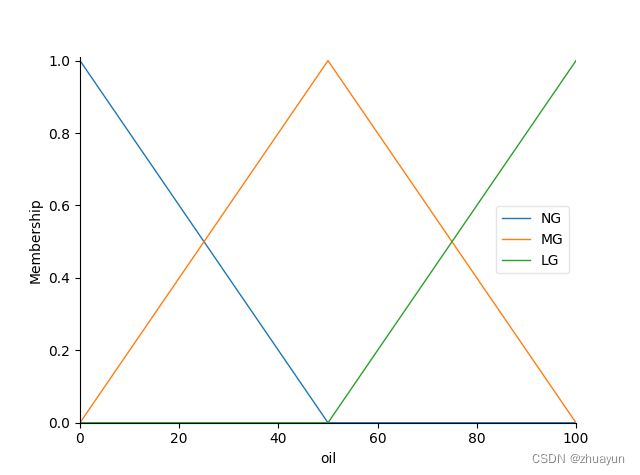
oil['NG'] = fuzz.trimf(x_oil, [0, 0, 50]) #定义油污的三角隶属度函数横坐标
oil['MG'] = fuzz.trimf(x_oil, [0, 50, 100])
oil['LG'] = fuzz.trimf(x_oil, [50, 100, 100])
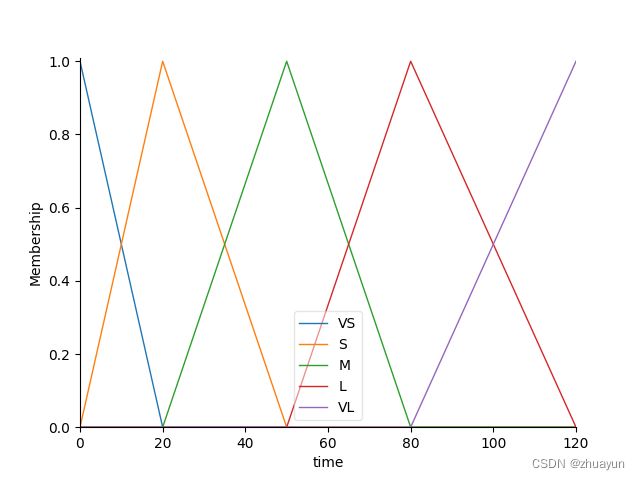
time['VS'] = fuzz.trimf(x_time, [0, 0, 20]) #定义洗涤时间的三角隶属度函数横坐标
time['S'] = fuzz.trimf(x_time, [0, 20, 50])
time['M'] = fuzz.trimf(x_time, [20, 50, 80])
time['L'] = fuzz.trimf(x_time, [50, 80, 120])
time['VL'] = fuzz.trimf(x_time, [80, 120, 120])
#采用解模糊方法——质心解模糊方式
time.defuzzify_method='centroid'
#规则
rule1=ctrl.Rule(antecedent=((stain['SD'] & oil['NG'])),consequent=time['VS'],label='time=VS')
rule2=ctrl.Rule(antecedent=((stain['SD'] & oil['MG'])|(stain['MD'] & oil['MG'])|(stain['LD'] & oil['NG'])),consequent=time['M'],label='time=M')
rule3=ctrl.Rule(antecedent=((stain['SD'] & oil['LG'])|(stain['MD'] & oil['LG'])|(stain['LD'] & oil['MG'])),consequent=time['L'],label='time=L')
rule4=ctrl.Rule(antecedent=((stain['MD'] & oil['NG'])),consequent=time['S'],label='time=S')
rule5=ctrl.Rule(antecedent=((stain['LD'] & oil['LG'])),consequent=time['VL'],label='time=VL')
# 系统和运行环境初始化
rule=[rule1, rule2, rule3,rule4,rule5]
time_ctrl = ctrl.ControlSystem(rule)
wash_time = ctrl.ControlSystemSimulation(time_ctrl)
#规则中带一些奇怪的规则,处理后输出
for i in range(len(rule)):
print("rule",i,end=":")
for item in str(rule[i]):
if(item!='\n'):
print(item,end="")
else:
break
print('\t')
#画图
stain.view()
oil.view()
time.view()
#time.view()
plt.show()
rule 0:IF stain[SD] AND oil[NG] THEN time[VS]
rule 1:IF ((stain[SD] AND oil[MG]) OR (stain[MD] AND oil[MG])) OR (stain[LD] AND oil[NG]) THEN time[M]
rule 2:IF ((stain[SD] AND oil[LG]) OR (stain[MD] AND oil[LG])) OR (stain[LD] AND oil[MG]) THEN time[L]
rule 3:IF stain[MD] AND oil[NG] THEN time[S]
rule 4:IF stain[LD] AND oil[LG] THEN time[VL]
#绘制3D图
upsampled=np.linspace(0,101,21)#步距参数
x,y=np.meshgrid(upsampled,upsampled)
z=np.zeros_like(x)
pp=[]
for i in range(0,21):
for j in range(0,21):
wash_time.input['stain']=x[i,j]
wash_time.input['oil']=y[i,j]
wash_time.compute()
z[i,j]=wash_time.output['time']
pp.append(z[i,j])
print('max:',max(pp))
print('min:',min(pp))
max: 106.66666666666666
min: 6.666666666666667
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure(figsize=(8,8))#画布大小
ax=fig.add_subplot(111,projection='3d')
surf=ax.plot_surface(x,y,z,rstride=1,cstride=1,cmap='viridis',linewidth=0.1,antialiased=True)
ax.view_init(30,250)#观察角度
plt.title('3D results')
ax.set_xlabel('stain')
ax.set_ylabel('oil')
ax.set_zlabel('time')
plt.show()
#输入输出
p=60#污渍的值
q=70#油污的值
wash_time.input['stain'] = int(p)
wash_time.input['oil'] = int(q)
wash_time.compute()
print ("洗涤时间为:",wash_time.output['time'])
洗涤时间为: 67.21682847896444