数据集-特征降维

1、降维

降维是指在某些限定条件下，降低随机变量(特征)个数，得到一组“不相关”主变量的过程

• 降低随机变量的个数
  
• 相关特征(correlated feature)
  • 相对湿度与降雨量之间的相关
  • 等等

正是因为在进行训练的时候，我们都是使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强，对于算法学习预测会影响较大

1.2、降维的两种方式

• 特征选择
• 主成分分析（可以理解一种特征提取的方式）

2、什么是特征选择

2.1、定义

数据中包含冗余或无关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

2.2、方法

• Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联
  • 方差选择法：低方差特征过滤
• Embedded (嵌入式)：算法自动选择特征（特征与目标值之间的关联）
  • 决策树:信息熵、信息增益
  • 正则化：L1、L2
  • 深度学习：卷积等

3、 过滤式

3.1、低方差特征过滤

• 删除低方差的一些特征，前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。

  • 特征方差小：某个特征大多样本的值比较相近
  • 特征方差大：某个特征很多样本的值都有差别

3.2、API

• sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
  • threshold：过滤多少小于多少阈值的数据
  • 删除所有低方差特征
  • Variance.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
    • 返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

3.3、代码

数据：数据集下载链接

示例：
index,pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expense,date,return
0,000001.XSHE,5.9572,1.1818,85252550922.0,0.8008,14.9403,1211444855670.0,2.01,20701401000.0,10882540000.0,2012-01-31,0.027657228229937388
1,000002.XSHE,7.0289,1.588,84113358168.0,1.6463,7.8656,300252061695.0,0.326,29308369223.2,23783476901.2,2012-01-31,0.08235182370820669
2,000008.XSHE,-262.7461,7.0003,517045520.0,-0.5678,-0.5943,770517752.56,-0.006,11679829.03,12030080.04,2012-01-31,0.09978900335112327
3,000060.XSHE,16.476,3.7146,19680455995.0,5.6036,14.617,28009159184.6,0.35,9189386877.65,7935542726.05,2012-01-31,0.12159482758620697
4,000069.XSHE,12.5878,2.5616,41727214853.0,2.8729,10.9097,81247380359.0,0.271,8951453490.28,7091397989.13,2012-01-31,-0.0026808154146886697

import pandas as pd
from sklearn.feature_selection import VarianceThreshold


def variance_demo():
    """
    删除低方差特征——特征选择
    :return: None
    """
    data = pd.read_csv("factor_returns.csv")
    print(data)
    # 1、实例化一个转换器类
    transfer = VarianceThreshold(threshold=10)
    # 2、调用fit_transform
    data = transfer.fit_transform(data.iloc[:, 1:10])  # index，date， return 三个不需要的特征
    print("删除低方差特征的结果：\n", data)
    print("形状：\n", data.shape)
    print(data)

    return None


if __name__ == '__main__':
    variance_demo()

结果：

            index  pe_ratio  pb_ratio  ...  total_expense        date    return
0     000001.XSHE    5.9572    1.1818  ...   1.088254e+10  2012-01-31  0.027657
1     000002.XSHE    7.0289    1.5880  ...   2.378348e+10  2012-01-31  0.082352
2     000008.XSHE -262.7461    7.0003  ...   1.203008e+07  2012-01-31  0.099789
3     000060.XSHE   16.4760    3.7146  ...   7.935543e+09  2012-01-31  0.121595
4     000069.XSHE   12.5878    2.5616  ...   7.091398e+09  2012-01-31 -0.002681
...           ...       ...       ...  ...            ...         ...       ...
2313  601888.XSHG   25.0848    4.2323  ...   1.041419e+10  2012-11-30  0.060727
2314  601901.XSHG   59.4849    1.6392  ...   1.089783e+09  2012-11-30  0.179148
2315  601933.XSHG   39.5523    4.0052  ...   1.749295e+10  2012-11-30  0.137134
2316  601958.XSHG   52.5408    2.4646  ...   6.009007e+09  2012-11-30  0.149167
2317  601989.XSHG   14.2203    1.4103  ...   4.132842e+10  2012-11-30  0.183629

[2318 rows x 12 columns]
删除低方差特征的结果：
 [[ 5.95720000e+00  8.52525509e+10  8.00800000e-01 ...  1.21144486e+12
   2.07014010e+10  1.08825400e+10]
 [ 7.02890000e+00  8.41133582e+10  1.64630000e+00 ...  3.00252062e+11
   2.93083692e+10  2.37834769e+10]
 [-2.62746100e+02  5.17045520e+08 -5.67800000e-01 ...  7.70517753e+08
   1.16798290e+07  1.20300800e+07]
 ...
 [ 3.95523000e+01  1.70243430e+10  3.34400000e+00 ...  2.42081699e+10
   1.78908166e+10  1.74929478e+10]
 [ 5.25408000e+01  3.28790988e+10  2.74440000e+00 ...  3.88380258e+10
   6.46539204e+09  6.00900728e+09]
 [ 1.42203000e+01  5.91108572e+10  2.03830000e+00 ...  2.02066110e+11
   4.50987171e+10  4.13284212e+10]]
形状：
 (2318, 7)

4、相关系数

• 皮尔逊相关系数(Pearson Correlation Coefficient)
  • 反映变量之间相关关系密切程度的统计指标

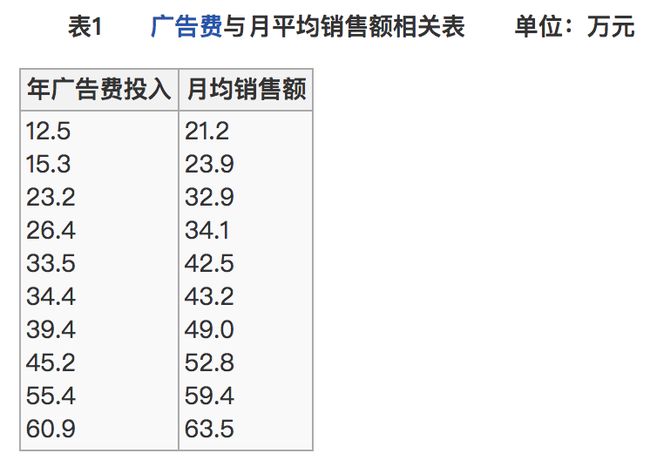
4.1、公式计算案例

• 比如说我们计算年广告费投入与月均销售额
  

那么之间的相关系数怎么计算
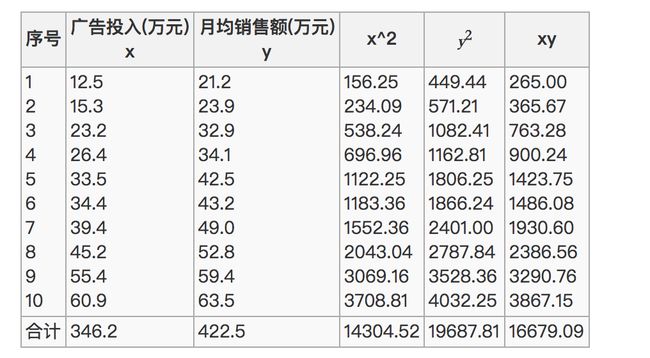最终计算：

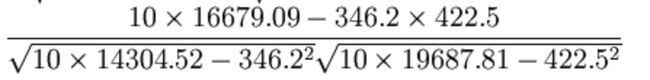
= 0.9942
所以我们最终得出结论是广告投入费与月平均销售额之间有高度的正相关关系。

4.2、特点

相关系数的值介于–1与+1之间，即–1≤ r ≤+1。其性质如下：

• 当r>0时，表示两变量正相关，r<0时，两变量为负相关
• 当|r|=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系
• 当0<|r|<1时，表示两变量存在一定程度的相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱
• 一般可按三级划分：|r|<0.4为低度相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关

这个符号：|r|为r的绝对值， |-5| = 5

4.3、API

• from scipy.stats import pearsonr
  • x : (N,) array_like
  • y : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)

import pandas as pd
from scipy.stats import pearsonr


def pearsonr_demo():
    """
    相关系数计算
    :return: None
    """
    data = pd.read_csv("factor_returns.csv")

    factor = ['pe_ratio', 'pb_ratio', 'market_cap', 'return_on_asset_net_profit', 'du_return_on_equity', 'ev',
              'earnings_per_share', 'revenue', 'total_expense']

    for i in range(len(factor)):
        for j in range(i, len(factor) - 1):
            print("指标%s与指标%s之间的相关性大小为%f" % (factor[i], factor[j + 1], pearsonr(data[factor[i]], data[factor[j + 1]])[0]))

    return None


if __name__ == '__main__':
    pearsonr_demo()

指标pe_ratio与指标pb_ratio之间的相关性大小为-0.004389
指标pe_ratio与指标market_cap之间的相关性大小为-0.068861
指标pe_ratio与指标return_on_asset_net_profit之间的相关性大小为-0.066009
指标pe_ratio与指标du_return_on_equity之间的相关性大小为-0.082364
指标pe_ratio与指标ev之间的相关性大小为-0.046159
指标pe_ratio与指标earnings_per_share之间的相关性大小为-0.072082
指标pe_ratio与指标revenue之间的相关性大小为-0.058693
指标pe_ratio与指标total_expense之间的相关性大小为-0.055551
指标pb_ratio与指标market_cap之间的相关性大小为0.009336
指标pb_ratio与指标return_on_asset_net_profit之间的相关性大小为0.445381
指标pb_ratio与指标du_return_on_equity之间的相关性大小为0.291367
指标pb_ratio与指标ev之间的相关性大小为-0.183232
指标pb_ratio与指标earnings_per_share之间的相关性大小为0.198708
指标pb_ratio与指标revenue之间的相关性大小为-0.177671
指标pb_ratio与指标total_expense之间的相关性大小为-0.173339
指标market_cap与指标return_on_asset_net_profit之间的相关性大小为0.214774
指标market_cap与指标du_return_on_equity之间的相关性大小为0.316288
指标market_cap与指标ev之间的相关性大小为0.565533
指标market_cap与指标earnings_per_share之间的相关性大小为0.524179
指标market_cap与指标revenue之间的相关性大小为0.440653
指标market_cap与指标total_expense之间的相关性大小为0.386550
指标return_on_asset_net_profit与指标du_return_on_equity之间的相关性大小为0.818697
指标return_on_asset_net_profit与指标ev之间的相关性大小为-0.101225
指标return_on_asset_net_profit与指标earnings_per_share之间的相关性大小为0.635933
指标return_on_asset_net_profit与指标revenue之间的相关性大小为0.038582
指标return_on_asset_net_profit与指标total_expense之间的相关性大小为0.027014
指标du_return_on_equity与指标ev之间的相关性大小为0.118807
指标du_return_on_equity与指标earnings_per_share之间的相关性大小为0.651996
指标du_return_on_equity与指标revenue之间的相关性大小为0.163214
指标du_return_on_equity与指标total_expense之间的相关性大小为0.135412
指标ev与指标earnings_per_share之间的相关性大小为0.196033
指标ev与指标revenue之间的相关性大小为0.224363
指标ev与指标total_expense之间的相关性大小为0.149857
指标earnings_per_share与指标revenue之间的相关性大小为0.141473
指标earnings_per_share与指标total_expense之间的相关性大小为0.105022
指标revenue与指标total_expense之间的相关性大小为0.995845

从中我们得出

• 指标revenue与指标total_expense之间的相关性大小为0.995845
• 指标return_on_asset_net_profit与指标du_return_on_equity之间的相关性大小为0.818697

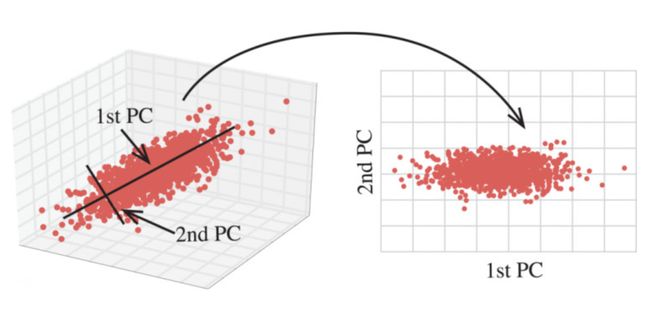
5、主成分分析

什么是主成分分析(PCA)

• 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量
• 作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
• 应用：回归分析或者聚类分析当中

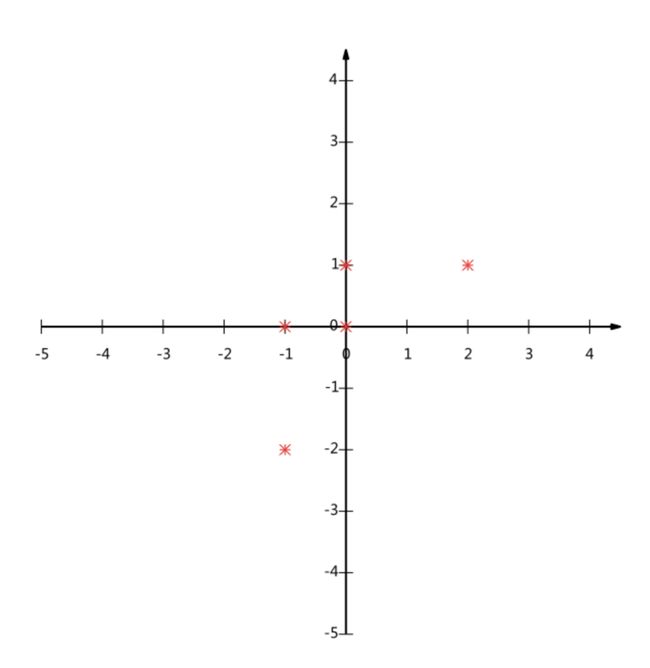
5.1、计算案例理解

假设对于给定5个点，数据如下

(-1,-2)
(-1, 0)
( 0, 0)
( 2, 1)
( 0, 1)

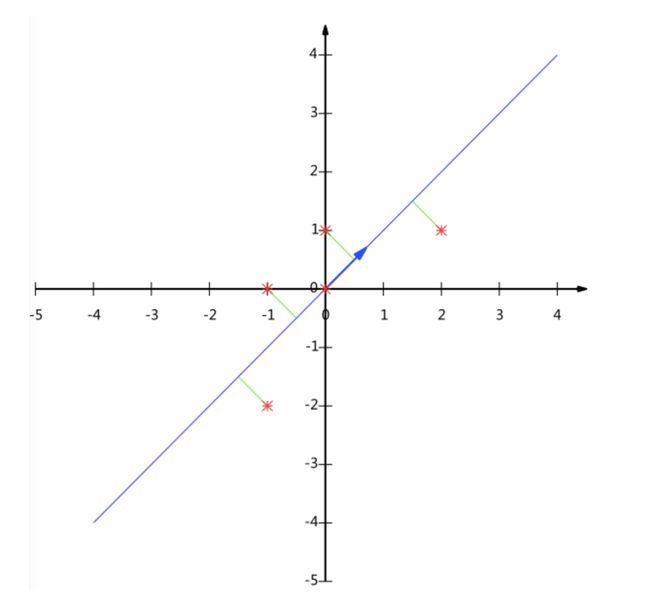
要求：将这个二维的数据简化成一维？ 并且损失少量的信息

这个过程如何计算的呢？找到一个合适的直线，通过一个矩阵运算得出主成分分析的结果（不需要理解）

5.2、API

• sklearn.decomposition.PCA(n_components=None)
  • 将数据分解为较低维数空间
  • n_components:
    • 小数：表示保留百分之多少的信息
    • 整数：减少到多少特征
  • PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
  • 返回值：转换后指定维度的array

5.3、数据计算

数据计算

[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]

from sklearn.decomposition import PCA


def pca_demo():
    """
    对数据进行PCA降维
    :return: None
    """
    data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]

    # 1、实例化PCA, 小数——保留多少信息
    transfer = PCA(n_components=0.9)
    # 2、调用fit_transform
    data1 = transfer.fit_transform(data)

    print("保留90%的信息，降维结果为：\n", data1)

    # 1、实例化PCA, 整数——指定降维到的维数
    transfer2 = PCA(n_components=3)
    # 2、调用fit_transform
    data2 = transfer2.fit_transform(data)
    print("降维到3维的结果：\n", data2)

    return None


if __name__ == '__main__':
    pca_demo()

保留90%的信息，降维结果为：
 [[ 1.28620952e-15  3.82970843e+00]
 [ 5.74456265e+00 -1.91485422e+00]
 [-5.74456265e+00 -1.91485422e+00]]
降维到3维的结果：
 [[ 1.28620952e-15  3.82970843e+00  5.26052119e-16]
 [ 5.74456265e+00 -1.91485422e+00  5.26052119e-16]
 [-5.74456265e+00 -1.91485422e+00  5.26052119e-16]]