OpenCV官方教程中文版 —— 图像金字塔

前言

• 学习图像金字塔

• 使用图像创建一个新水果：“橘子苹果”

• 将要学习的函数有：cv2.pyrUp()，cv2.pyrDown()。

一、原理

一般情况下，我们要处理是一副具有固定分辨率的图像。但是有些情况下，我们需要对同一图像的不同分辨率的子图像进行处理。比如，我们要在一幅图像中查找某个目标，比如脸，我们不知道目标在图像中的尺寸大小。这种情况下，我们需要创建创建一组图像，这些图像是具有不同分辨率的原始图像。我们把这组图像叫做图像金字塔（简单来说就是同一图像的不同分辨率的子图集合）。如果我们把最大的图像放在底部，最小的放在顶部，看起来像一座金字塔，故而得名图像金字塔。

有两类图像金字塔：高斯金字塔和拉普拉斯金字塔。

高斯金字塔的顶部是通过将底部图像中的连续的行和列去除得到的。顶部图像中的每个像素值等于下一层图像中 5 个像素的高斯加权平均值。这样操作一次一个 MxN 的图像就变成了一个 M/2xN/2 的图像。所以这幅图像的面积就变为原来图像面积的四分之一。这被称为 Octave。连续进行这样的操作我们就会得到一个分辨率不断下降的图像金字塔。我们可以使用函数cv2.pyrDown() 和 cv2.pyrUp() 构建图像金字塔。

函数 cv2.pyrDown() 从一个高分辨率大尺寸的图像向上构建一个金子塔（尺寸变小，分辨率降低）。

# -*- coding:utf-8 -*-
import cv2 as cv

# 高斯金字塔
def pyramid_demo(image):
    level = 4  # 金字塔的层数
    temp = image.copy()  # 拷贝图像
    pyramid_images = []
    for i in range(level):
        dst = cv.pyrDown(temp)  # down是降采样-尺寸变小，分辨率降低（缩小）
        pyramid_images.append(dst)
        cv.imshow("pyramid" + str(i), dst)
        temp = dst.copy()
    return pyramid_images

src = cv.imread("ball.png")
cv.namedWindow('input image', cv.WINDOW_NORMAL)
cv.imshow("input image", src)
pyramid_demo(src)
cv.waitKey(0)
cv.destroyAllWindows()

下图是一个四层的图像金字塔。

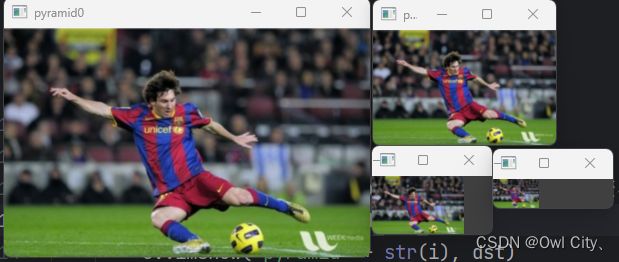
函数 cv2.pyrUp() 从一个低分辨率小尺寸的图像向下构建一个金子塔（尺寸变大，但分辨率不会增加）。

higher_reso2 = cv2.pyrUp(lower_reso)

你要记住的是是 higher_reso2 和 higher_reso 是不同的。因为一旦使用 cv2.pyrDown()，图像的分辨率就会降低，信息就会被丢失。下图就是从 cv2.pyrDown() 产生的图像金字塔的（由下到上）第三层图像使用函数cv2.pyrUp() 得到的图像，与原图像相比分辨率差了很多。

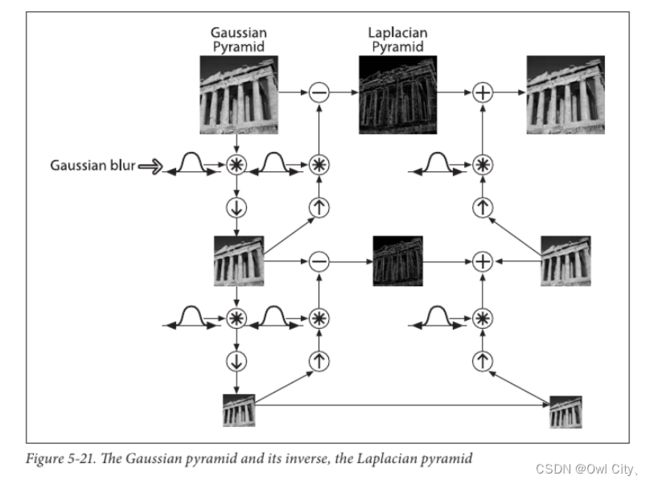
拉普拉斯金字塔可以有高斯金字塔计算得来，公式如下：

拉普拉金字塔的图像看起来就像边界图，其中很多像素都是 0。他们经常被用在图像压缩中。下图就是一个三层的拉普拉斯金字塔：

# -*- coding:utf-8 -*-
import cv2 as cv
# 高斯金字塔
def pyramid_demo(image):
    level = 4  # 金字塔的层数
    temp = image.copy()  # 拷贝图像
    pyramid_images = []
    for i in range(level):
        dst = cv.pyrDown(temp)  # down是降采样-尺寸变小，分辨率降低（缩小）
        pyramid_images.append(dst)
        cv.imshow("pyramid" + str(i), dst)
        temp = dst.copy()
    return pyramid_images


# 拉普拉斯金字塔，拉普拉斯金字塔时，图像大小必须是2的n次方*2的n次方，不然会报错
def laplian_demo(image):
    pyramid_images = cv.resize(image, (512, 512), interpolation=cv.INTER_CUBIC)  # 可以替换成INTER_LINEAR
    pyramid_images = pyramid_demo(pyramid_images)
    level = len(pyramid_images)  # 4 层
    for i in range(level-1, 0, -1):  # 每次递减
        expand = cv.pyrUp(pyramid_images[i], dstsize=pyramid_images[i - 1].shape[:2])
        lpls = cv.subtract(pyramid_images[i - 1], expand)
        cv.imshow("lpls_down" + str(i), lpls)

def pyramid_demo_2(image):
    higher_reso2 = cv.pyrUp(image)
    cv.imshow("pyramid", higher_reso2)
    return higher_reso2

src = cv.imread("ball.png")
src2 = cv.imread("lower_reso.png")
cv.namedWindow('input image', cv.WINDOW_NORMAL)
cv.imshow("input image", src)
#pyramid_demo(src)
#pyramid_demo_2(src2)
laplian_demo(src)
cv.waitKey(0)
cv.destroyAllWindows()

二、使用金字塔进行图像融合

图像金字塔的一个应用是图像融合。例如，在图像缝合中，你需要将两幅图叠在一起，但是由于连接区域图像像素的不连续性，整幅图的效果看起来会很差。这时图像金字塔就可以排上用场了，他可以帮你实现无缝连接。这里的一个经典案例就是将两个水果融合成一个，看看下图也许你就明白我在讲什么了。

你可以通过阅读后边的更多资源来了解更多关于图像融合，拉普拉斯金字塔的细节。实现上述效果的步骤如下：

1. 读入两幅图像，苹果和橘子
2. 构建苹果和橘子的高斯金字塔（6 层）
3. 根据高斯金字塔计算拉普拉斯金字塔
4. 在拉普拉斯的每一层进行图像融合（苹果的左边与橘子的右边融合）
5. 根据融合后的图像金字塔重建原始图像。

整个过程的代码如下。（为了简单，每一步都是独立完成的，这回消耗更多的内存，如果你愿意的话可以对他进行优化）

# -*- coding: utf-8 -*-
import cv2
from matplotlib import pyplot as plt
import numpy as np

A = cv2.imread('apple.png')
A = cv2.resize(A, (256, 256), interpolation=cv2.INTER_CUBIC)  # 可以替换成INTER_LINEAR
B = cv2.imread('orange.png')
B = cv2.resize(B, (256, 256), interpolation=cv2.INTER_CUBIC)  # 可以替换成INTER_LINEAR
b, g, r = cv2.split(A)
A = cv2.merge([r, g, b])
b, g, r = cv2.split(B)
B = cv2.merge([r, g, b])

# generate Gaussian pyramid for A
G = A.copy()
gpA = [G]
for i in range(6):
    G = cv2.pyrDown(G)
    gpA.append(G)

# generate Gaussian pyramid for B
G = B.copy()
gpB = [G]
for i in range(6):
    G = cv2.pyrDown(G)
    gpB.append(G)

# generate Laplacian Pyramid for A
lpA = [gpA[5]]
for i in range(5, 0, -1):
    GE = cv2.pyrUp(gpA[i])
    L = cv2.subtract(gpA[i - 1], GE)
    lpA.append(L)

# generate Laplacian Pyramid for B
lpB = [gpB[5]]
for i in range(5, 0, -1):
    GE = cv2.pyrUp(gpB[i])
    L = cv2.subtract(gpB[i - 1], GE)
    lpB.append(L)

# Now add left and right halves of images in each level
# numpy.hstack(tup)
# Take a sequence of arrays and stack them horizontally
# to make a single array.

LS = []
for la, lb in zip(lpA, lpB):
    rows, cols, dpt = la.shape
    ls = np.hstack((la[:, 0:int(cols / 2)], lb[:, int(cols / 2):]))
    LS.append(ls)

# now reconstruct
ls_ = LS[0]
for i in range(1, 6):
    ls_ = cv2.pyrUp(ls_)
    ls_ = cv2.add(ls_, LS[i])

# image with direct connecting each half
real = np.hstack((A[:, :int(cols / 2)], B[:, int(cols / 2):]))

plt.figure()
plt.subplot(221)
plt.imshow(A)  # expects distorted color
plt.xticks([]), plt.yticks([])  # to hide tick values on X and Y axis
plt.title("apple")
plt.subplot(222)
plt.imshow(B)  # expect true color
plt.xticks([]), plt.yticks([])  # to hide tick values on X and Y axis
plt.title("orange")
plt.subplot(223)
plt.imshow(real)  # expect true color
plt.xticks([]), plt.yticks([])  # to hide tick values on X and Y axis
plt.title("Direct_connection")
plt.subplot(224)
plt.imshow(ls_)  # expect true color
plt.xticks([]), plt.yticks([])  # to hide tick values on X and Y axis
plt.title("Pyramid_blending")
plt.show()