二叉树进阶
欢迎来到Cefler的博客
博客主页:那个传说中的man的主页
个人专栏:题目解析
推荐文章:题目大解析(3)
目录
- 二叉搜索树
-
- 概念
- 二叉搜索树模拟实现
-
- Insert插入
- find查找
- 中序遍历
- Erase删除
- InsertR递归插入
- FindR递归查找
- EraseR递归删除
- BinarySearchTree.h
二叉搜索树
概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
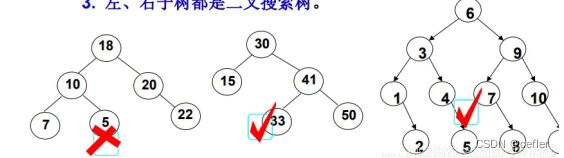
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
即:左<根<右
二叉搜索树模拟实现
Insert插入
bool Insert(const K& key)
{
if (_root == nullptr)//如果为空直接创建新结点
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)//key比当前cur结点的key值小往左边走,大则往右边走,直到遇到空
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);//此时遇到空要创建新结点
//但此时我们还要记得将其与parent连接起来,至于是在parent的左边还是右边,看比大小
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
过程即为:小于往左走,大于往右走,遇到空创建新结点,进行连接父节点
find查找
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
return true;//相等说明找到,返回true
}
return false;
}
中序遍历
void _InOrder(Node* root)//中序遍历
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
void InOrder()//套一层
{
_InOrder(_root);
cout << endl;
}
Erase删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
而a情况可以归属于b和c任意一个情况,a情况当把结点删除后,父节点想向指向左右哪边都行,反正都为空无所谓。
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点
中,再来处理该结点的删除问题–替换法删除
替换法删除:
1.要么从左子树中找到最大结点来替换
2.要么从右子树找到最小结点来替换
所以现在梳理一下代码思路:
1.先找到要删除的结点位置,能找到再删除,找不到返回false
2.开始删除,判情况(b,c,d),对症下药
代码如下:
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)//寻找要删除的结点
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
//找到了就可以开始删除了,但是要判情况,对症下药
if (cur->_left == nullptr)
{
//左边为空,则删除后,将父节点连接cur的右边
if (cur == _root)//如果要删除的结点就是初始根结点
{
_root = cur->_right;
}
//先确定此时cur在父节点的左边还是右边
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else if (cur->_right == nullptr)
{
//右边为空
if (cur == _root)//如果要删除的结点就是初始根结点
{
_root = cur->_left;
}
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
//左右都不为空,此时用替换法
//这里我们以寻找右边树最小值的替换法执行;而右边树最小值即可以认为就是右边树最左边结点
Node* parent = cur;
Node* subleft = cur->_right;
while (subleft->_left)//当左边遇到空,说明此时subleft已经遍历到最左边
{
parent = subleft;
subleft = subleft->_left;
}
//找到后,可以进行交换了
swap(cur->_key, subleft->_key);
//现在进行删除,而且删除情况属于a情况
if (subleft == parent->_left)
{
parent->_left = subleft->_right;//这边=subleft->_right或者subleft->_left都可以
}
else
{
parent->_right = subleft->_right;
}
}
return true;
}
}
return false;
}
InsertR递归插入
bool _InsertR(Node*& root, const K& key)//递归插入
{
if (root == nullptr)
{
root = new Node(key);//传引用的好处就是此时的root就是其父节点的左/右节点,无需记录父节点
return true;
}
if (root->_key > key)
{
_InsertR(root->_left, key);
}
else if (root->_key < key)
{
_InsertR(root->_right, key);
}
else
return false;
}
FindR递归查找
bool _FindR(Node* root, const K& key)//递归查找
{
if (root == nullptr)
return false;
if (root->_key > key)
{
FindR(root->_left, key);
}
else if (root->_key < key)
{
FindR(root->_right, key);
}
else
return true;
}
EraseR递归删除
bool _EraseR(Node*& root, const K& key)//这里我们仍然用引用root,这样连接时就不用记录父节点了
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
//开始删除
if (root->_left == nullptr)
{
//左为空
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
//左右都不为空
//这里以寻找右子树最小值
Node* subleft = root->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
swap(root->_key, subleft->_key);
// 转换成在子树去递归删除
return _EraseR(root->_right, key);
}
}
}
BinarySearchTree.h
#pragma once
#include 如上便是本期的所有内容了,如果喜欢并觉得有帮助的话,希望可以博个点赞+收藏+关注❤️ ,学海无涯苦作舟,愿与君一起共勉成长