JAVA排序

再看各种排序前我们先了解一下什么叫 稳定性

比如一组数据arr[i]下标与arr[j下标]相等,arr[i]在前面,arr[j]在arr[i]后面,排序后这两个数据仍然是arr[i]在arr[j]前面,arr[j]在arr[i]后面,这就叫稳定

插入排序：

优势:  越有序查找速度越快

时间复杂度:  O(N^2)

空间复杂度:  O(1)

稳定性：稳定

public void insertSort(int[] arr){
        //i负责引路,j负责把i后面的数据都变得有序
        for(int i = 1; i < arr.length; i++){
            for(int j = i - 1; j >= 0; j--){
                //想想为什么不是arr[j] > arr[i]:因为j会变化
                if(arr[j] > arr[j+1]){
                    //交换
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                }else{
                    break;
                }
            }
        }
    }

希尔排序:(插入排序的优化)

将所有数据进行分组,先分成许多组,这样每组数据就会变少,在将组的数据排序,

即使时间复杂度是O(N^2)也没事,因为数据少,就算N的平方也没多少

然后逐渐减少组的数量，每组的数据就会变多，但数据越趋近于有序，所以查找速度越快(因为插入排序数据越趋于有序查找速度越快)

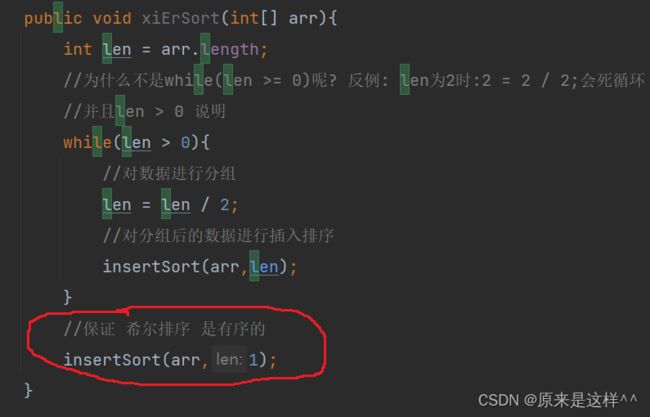
最后让 insertSort(arr,1)是为了确保让 希尔排序 排序成功

 public void xiErSort(int[] arr){
        int len = arr.length;
        //为什么不是while(len >= 0)呢? 反例: len为2时:2 = 2 / 2;会死循环
        //并且len > 0 说明
        while(len > 0){
            //对数据进行分组
            len = len / 2;
            //对分组后的数据进行插入排序
            insertSort(arr,len);
        }
        //保证 希尔排序 是有序的
        insertSort(arr,1);
    }

    private void insertSort(int[] arr,int len){
        for(int i = len; i < arr.length; i++){
            for(int j = i - len; j >= 0; j = j - len){
                 if(arr[j] > arr[j+len]){
                     //交换
                     int tmp = arr[j];
                     arr[j] = arr[j+len];
                     arr[j+len] = tmp;
                 }else{
                     break;
                 }
            }
        }
    }

问个问题:为何 xiEr方法里的最后要加一段insertSort(arr,1)?

答:为了让希尔排序是彻彻底底有序的,这样虽然看起来和插入排序一样,但因为经过前面的代码数据已经趋于有序,所以最后加个插入排序其实时间复杂度也不高

测试插入排序和希尔排序(插入排序的优化)排序时间对比

可以看到希尔排序比插入排序快很多

选择排序:

时间复杂度: O(n^2)

空间复杂度:  O(1)

稳定性:  不稳定

思路:找到数组里的最小值和最左边i下标交换,如何i++,继续找i后面的最小值然后和i交换,这样就能从小到大排序了

 //选择排序
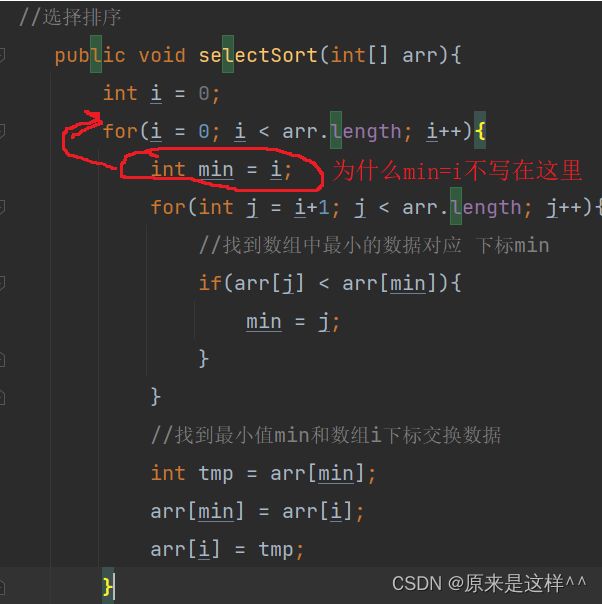
    public void selectSort(int[] arr){
        int i = 0;
        for(i = 0; i < arr.length; i++){
            int min = i;
            for(int j = i+1; j < arr.length; j++){
                //找到数组中最小的数据对应 下标min
                if(arr[j] < arr[min]){
                    min = j;
                }
            }
            //找到最小值min和数组i下标交换数据
            int tmp = arr[min];
            arr[min] = arr[i];
            arr[i] = tmp;
        }

问个问题:为什么min不写在这里?

原因是为了让min变量不断变化将数组里的最小值按从小到大顺序排好,放在箭头所指位置就不变化了,也就是说只能将数据放在相同的位置不动

选择排序的优化:

之前是找到最小值就换位置,那我能不能一次找到最小值和最大值再换位置?将最小值换到数据偏左的位置,将最大值放到数据偏右边的位置

为什么呢?原因是 如果 最大值MAX = left的时候就会把原来的最大值下标移到其它下标处(听懂掌声)

正确的 选择排序优化

    //选择排序的优化方案
    //之前是找到最小值就换位置,那我能不能一次找到最小值和最大值再换位置?将最小值换到数据偏左的位置,将最大值放到数据偏大的位置
    public void selectSort2(int[] arr){
        //left放最小,right放最大值
        int left = 0;
        int right = arr.length - 1;
        while(left < right){
            //用来放最大值和最小值下标
            int MAX = left;
            int min = left;
            //j下标用来找数据
            for(int j = left + 1; j <= right; j++){
                //找最大值
                if(arr[j] > arr[MAX]){
                    MAX = j;
                }
                //找最小值
                if(arr[j] < arr[min]){
                    min = j;
                }
            }
            //最小值和数组left下标交换
            swap(arr,left,min);
            //如果最大值MAX在left处的话由于left交换后最大值位置变为min下标了
            if(MAX == left){
                MAX = min;
            }
            swap(arr,right,MAX);
            //left++用来找下一个最小数据
            //right--用来找下一个最大数据
            right--;
            left++;
        }
    }

    //用来交换数据位置
    private void swap(int[] arr,int i,int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

为什么范围是 j <= right,而不是 j < arr.length()
因为如果判定范围在 j < arr.length() 的话下面的代码就会把
原本在右边放好最大值 重新掉换成错误位置位置

快速排序(挖坑法:未优化)

时间复杂度O(N*logN)

空间复杂度O(logN)

大体上是找到一个 基准点,基准点的左边得数据都比基准点小,基准点的右边数据都比基准点大

然后递归分成左树和右树

  //快速排序(挖坑法:未优化)
    //为了接口的和其他的一样我们参数就设为int[] arr
    public void quickSort(int[] arr){
        quickSort_(arr,0,arr.length-1);
    }

    public void quickSort_(int[] arr,int left,int right){
        //为什么是left >= right就结束,而不是left > right呢?
        //因为当 left == right 就说明 左边或右边只有一个数字呢,一个数字必然是有序的
        if(left >= right){
            return;
        }
        int index = centreIndex(arr,left,right);
        //这样 左边 就比基准值index小了, 右边 比基准值大
        //将数组按基准值的左边划为左树,基准值的右边划分为右树
        //左边
        quickSort_(arr,left,index - 1);
        //右边
        quickSort_(arr,index+1,right);
    }

    //找到基准下标位置
    public int centreIndex(int[] arr,int left,int right){
        int tmp = arr[left];
        while(left < right){
            //找到右边比基准值小的数
            while(left < right && arr[right] >= tmp){
                right--;
            }
            //右边遇到比基准值小的,和左边left换位置
            swap(arr,left,right);

            //找到左边比基准值大的数
            while(left < right && arr[left] <= tmp){
                left++;
            }
            //左边遇到比基准值大的,和右边right换位置
            swap(arr,left,right);
        }
        //出到这里说明 left == right
        if(left == right){
            arr[left] = tmp;
        }
        return left;
    }

    //用来交换数据位置
    private void swap(int[] arr,int i,int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

问?为什么红圈圈起来的都使用的是 >=

答:第一处if(left >= right) 中 判断条件是 >= 是因为 当left == right的时候说明在递归到最后left == riight的时候说明 只有一个数字,一个数字不管怎么样都是有序的

第二处第三处的while(left < right && arr[left] >= tmp)是为了防止死循环,如果数据像下面数组一样没有>=就死循环了

问:为什么在找基准值方法centreIndex_()里的while(left < right && arr[left] >= tmp)while循环里有while(left < right),原因还是上面那幅图,为了防止数组下标越界

快速排序的优化1

1.为了防止数组里的数据是有序而出现单分支的情况,我们会先使用三数取中的方法将数组里的数据打乱,使得数组里的数据无法有序,从而快速排序也不会出现单分支的情况了

光是左树或右树复杂度是最高的

快速排序优化2

1.我们使用快速排序时快到最后发现最后树的节点是最多的,但整体趋近于有序,并且最后一两层就占据了整个数据的60%甚至70%,所以我们可以在快速排序的最后一两层使用 插入排序 的方法来优化, 插入排序的特点就是 数组越有序,插入排序效果越快

  //快速查找(挖坑法:优化1)
    //优化它是单分支的数据
    public void quickSort2(int[] arr){
        quickSort_2(arr,0,arr.length - 1);
    }

    private void quickSort_2(int[] arr,int left,int right){
        if(left >= right){
            return;
        }
        //为了防止出现数组有序而出现的 单分支的情况
//        使用 三数去中法
        int centreIndex = num(arr,left,right);
        //swap(arr,0,centreIndex)
        swap(arr,left,centreIndex);
        //调换完成就不会出现 数组有序而出现的 单分支 的情况啦


        //找基准值
        int index = centreIndex2(arr,left,right);
        //递归左树 和右树
        quickSort_2(arr,left,index-1);
        quickSort_2(arr,index+1,right);


    }

    //基准值
    private int centreIndex2(int[] arr,int left,int right){
        int tmp = arr[left];
        while(left < right){
            while(left < right && arr[right] >= tmp){
                right--;
            }
            swap(arr,left,right);
            while(left = left; j--){
                if(arr[j] > arr[j+1]){
                    //第一个比第二个大,交换
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                }
            }
        }
    }

优化快速排序需要注意的点

使用双指针法进行快速排序

思路：和普通快速排序的思路差不多,先找基准值,基准值的左边小于基准值,基准值的右边大于基准值,然后使用递归直到left >= right时结束,双指针快速排序主要与普通快排就是使用了双指针的方法进行找基准值

  public static void double_index(int[] arr){
        if(arr.length == 0){
            return;
        }
        double_Index(arr,0,arr.length-1);
    }

    private static void double_Index(int[] arr, int left, int right) {
        if(left >= right){
            return;
        }
        //找基准
        int index = find_Index(arr,left,right);
        double_Index(arr,left,index - 1);
        double_Index(arr,index+1,right);
    }

    //找基准值
    private static int find_Index(int[] arr, int left, int right) {
        int tmp = arr[left];
        int slow = left;
        int fast = slow + 1;

        for(fast = slow + 1; fast <= right; fast++){
            if(arr[fast] < tmp){
                slow++;
                if(slow != fast){
                    swap(arr,slow,fast);
                }
            }
        }
        swap(arr,left,slow);
        return slow;
    }

    private static void swap(int[] arr, int slow, int fast) {
        int tmp = arr[slow];
        arr[slow] = arr[fast];
        arr[fast] = tmp;
    }

双指针主要看这几行代码

slow指针永远指向数组里比tmp小的最后一个数据,而fast指针则是数组里找比tmp小的数据

堆排序

先根据数组创建成一个堆

从小到大排序就创建成大根堆,从大到小排序就创建成小根堆

创建完堆后就将 堆顶元素 和 堆的末尾元素 调换位置,这样堆顶元素(最大的)就放到最后,然后在将调换的堆顶元素重新建成大根堆,在继续调换,这样就会形成一个从小到大排序的数组

  public static void prioritySort(int[] arr){
        if(arr.length == 0){
            return;
        }
        //首先先拿这个数组用来创建一个堆
        //从小到大排序的话就创建 大根堆
        //从大到小排序的话就创建 小根堆
        for (int father = (arr.length - 1) / 2; father >= 0; father--) {
            create(arr,father,arr.length);
        }
        int len = arr.length;
        //排序
        while(len > 0){
            //交换
            int tmp = arr[0];
            arr[0] = arr[len-1];
            arr[len-1] = tmp;
            len--;
            //重新将换了的堆顶元素变为 大根堆
            create(arr,0,len);
//            len--;
        }
    }
    //从小到大排序(创建大根堆)
    private static void create(int[] arr,int father,int len){
        int child = (father * 2)+1;
        while(child < len){
            //找到最大的孩子节点
            if(child+1 < len && arr[child+1] > arr[child]){
                child++;
            }
            //这样child指向的就是最大的孩子节点了
            //最大的孩子节点 和 父亲节点比较
            if(arr[child] > arr[father]){
                //交换
                int tmp = arr[father];
                arr[father] = arr[child];
                arr[child] = tmp;
                father = child;
                child = (father * 2)+1;
//                child = father;
//                father = (child-1)/2;
            }else{
                break;
            }
        }
    }

冒泡排序:感觉没什么好讲的这个：一般不会用它

    //冒泡排序(优化)
    public static void Sort2(int[] arr){
        for(int i = 0; i < arr.length; i++){
            boolean judge = false;
            for(int j = 0; j < arr.length-1-i; j++){
                if(arr[j] > arr[j+1]){
                    //交换
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                    judge = true;
                }//else {
                 //   break
                //}
            }
            if(!judge){
                return;
            }
        }
    }