二叉树链式结构的实现
文章目录
- 二叉树的遍历
-
- 前序遍历
- 中序遍历:
- 后序遍历
- 节点个数及高度等
-
- 求二叉树节点个数
- 求二叉树叶子节点个数
- 求二叉树第k层节点个数
- 求二叉树深度/高度
- 查找值为x的节点
- 二叉树基础oj练习
-
- 单值二叉树
- 二叉树的前序遍历
- 相同的树
- 对称二叉树
- 另一棵树的子树
- 二叉树的创建和销毁
-
- 通过前序遍历的数组构建二叉树
- 二叉树销毁
- 层序遍历
- 判断是否是完全二叉树
二叉树的遍历
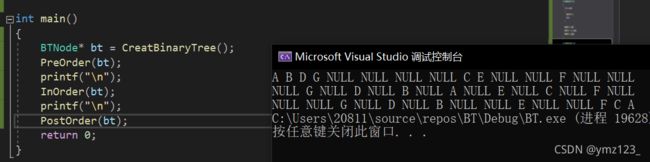
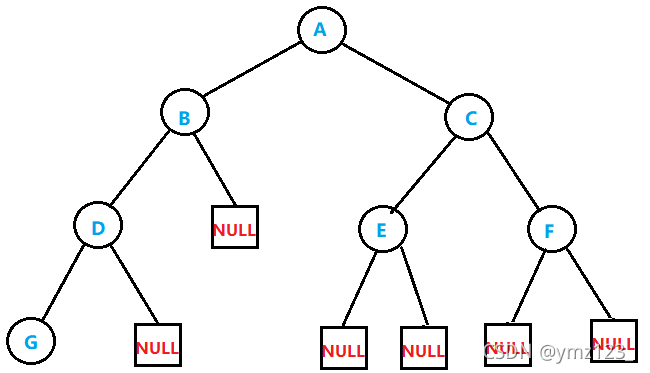
为了先了解二叉树的结构,此处先手动快速创建一棵简单的二叉树:
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
node->_data = x;
node->_left = NULL;
node->_right = NULL;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode('A');
BTNode* node2 = BuyNode('B');
BTNode* node3 = BuyNode('C');
BTNode* node4 = BuyNode('D');
BTNode* node5 = BuyNode('E');
BTNode* node6 = BuyNode('F');
BTNode* node7 = BuyNode('G');
node1->_left = node2;
node1->_right = node3;
node2->_left = node4;
node3->_left = node5;
node3->_right = node6;
node4->_left = node7;
return node1;
}
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->_data);
PreOrder(root->_left);
PreOrder(root->_right);
}
中序遍历:
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->_left);
printf("%c ", root->_data);
InOrder(root->_right);
}
后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}
节点个数及高度等
求二叉树节点个数
核心思想:节点个数=1+左子树节点个数+右子树节点个数
int BinaryTreeSize(BTNode* root)
{
return root==NULL?0:1
+BinaryTreeSize(root->_left)
+ BinaryTreeSize(root->_right);
}
求二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
else if (root->_left == NULL && root->_right == NULL)
return 1;
else
return BinaryTreeLeafSize(root->_left)
+ BinaryTreeLeafSize(root->_right);
}
求二叉树第k层节点个数
核心思路:当前树的第k层节点个数=当前树的左子树的第k-1层个数+当前树的右子树的第k-1层个数
int BinaryTreeLeavelKSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
else if (k == 1)
return 1;
else
return BinaryTreeLeavelKSize(root->_left,k-1)
+ BinaryTreeLeavelKSize(root->_right,k-1);
}
求二叉树深度/高度
核心思想:当前树的深度=max(左子树深度,右子树深度)+1
int BinaryTreeDepth(BTNode* root)
{
if (root == NULL)
return 0;
//先给两个变量存储结果,若直接放到return就得算两次
int leftDepth = BinaryTreeDepth(root->_left);
int rightDepth = BinaryTreeDepth(root->_right);
return leftDepth > rightDepth?leftDepth+1:rightDepth+1;
}
查找值为x的节点
- 先判断是不是当前节点,是就返回
- 不是就先去左树找,找到了就返回
- 左树没找到,再去右树找。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->_data == x)
return root;
BTNode* left = BinaryTreeFind(root->_left, x);
if (left)
return left;
BTNode* right = BinaryTreeFind(root->_right, x);
if(right)
return right;
return NULL;
}
二叉树基础oj练习
分治:大问题分成小问题,小问题再继续分,直到分割成不可再分割的子问题。
单值二叉树
题目描述:如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时,才返回true,否则返回false
思路:
- ==具有传递性
- a == b && a == c
- b == e && b == f
- 即a跟e和f相等。
bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
return true;
if(root->left && root->val != root->left->val)
return false;
if(root->right && root->val != root->right->val)
return false;
return isUnivalTree(root->left)
&& isUnivalTree(root->right);
}
其中if(root->left && root->val != root->left->val) &&两边不能调换,否则如果root->left为空,但却已经进行了两个值的比较,会报错。
二叉树的前序遍历
题目描述:给你二叉树的根节点root,返回它节点值的前序遍历
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int TreeSize(struct TreeNode* root)
{
if(root==NULL)
return 0;
return 1+TreeSize(root->left)+TreeSize(root->right);
}
void _preorderTraversal(struct TreeNode* root,int* arr,int* pi)
{
if(root==NULL)
return;
arr[(*pi)++]=root->val;
_preorderTraversal(root->left,arr,pi);
_preorderTraversal(root->right,arr,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
*returnSize=TreeSize(root);
int* arr=(int*)malloc(sizeof(int)* *returnSize);
int i=0;
_preorderTraversal(root,arr,&i);
return arr;
}
注意: 在void _preorderTraversal中,最后一个参数要传的是指针。每个递归调用栈帧中都有一个i,下一层++i,不会对上一次影响。但是我们想要的是只有一个i作为下标++
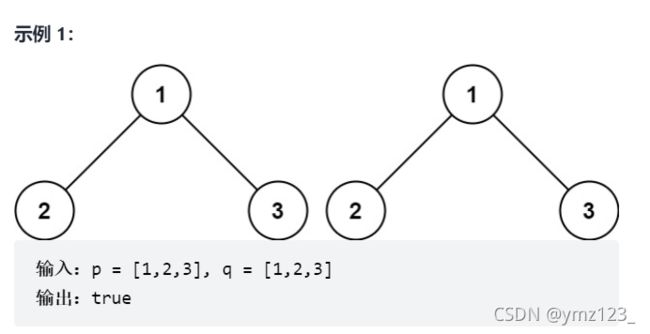
相同的树
题目描述:给你两棵二叉树的根节点p和q,编写一个函数来检验这两棵树是否相同。如果两个数在结构上相同,并且节点具有相同的值,则认为它们是相同的。
要比较两棵树是否相同,就要比较两棵树的根节点和各自的左子树和右子树是否相同。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p==NULL && q==NULL)
return true;
if(p==NULL || q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}
- 时间复杂度:O(N)
- 空间复杂度:O(h)-> 最坏情况 O(N) 完全二叉树或满二叉树h=logN
对称二叉树
要判断是否对称,首先判断根节点是否为空,再判断根节点的左右子树是否对称,递归。
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q)
{
if(p==NULL && q==NULL)
return true;
if(p==NULL || q==NULL)
return false;
if(p->val!=q->val)
return false;
return _isSymmetric(p->left,q->right)
&& _isSymmetric(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root){
if(root==NULL)
return true;
return _isSymmetric(root->left,root->right);
}
另一棵树的子树
题目描述:给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root==NULL)
return false;
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);
}
二叉树的创建和销毁
通过前序遍历的数组构建二叉树
问题描述:编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
struct TreeNode
{
char val;
struct TreeNode* left;
struct TreeNode* right;
};
struct TreeNode* CreatTree(char* str,int* pi)
{
if(str[*pi]=='#')
{
(*pi)++;
return NULL;
}
struct TreeNode* root=(struct TreeNode*)
malloc(sizeof(struct TreeNode));
root->val=str[(*pi)++];
root->left=CreatTree(str, pi);
root->right=CreatTree(str, pi);
return root;
}
void InOrder(struct TreeNode* root)
{
if(root==NULL)
return;
InOrder(root->left);
printf("%c ",root->val);
InOrder(root->right);
}
int main()
{
char str[100];
scanf("%s",str);
int i=0;
struct TreeNode* root=CreatTree(str, &i);
InOrder(root);
return 0;
}
二叉树销毁
//二叉树销毁
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestroy(root->_left);
BinaryTreeDestroy(root->_right);
free(root);
}
层序遍历
用队列实现二叉树的层序遍历。先把第一次(根)放入队列。上一层出队,带入下一层。
//层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->_data);
if (front->_left)
{
QueuePush(&q,front->_left);
}
if (front->_right)
{
QueuePush(&q, front->_right);
}
}
printf("\n");
QueueDestroy(&q);
}
判断是否是完全二叉树
核心思路: 层序遍历,把空的节点也入队列。如果是完全二叉树,非空节点是连续的,空也是连续的。如果不是完全二叉树,非空节点不连续,空也不连续。
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front==NULL)
{
break;
}
QueuePush(&q, front->_left);
QueuePush(&q, front->_right);
}
//找到空后,队列中全是空,就是完全二叉树
//还有非空,就不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}