数字图像处理 第八章图像压缩

引言

图像压缩是一种减少描绘一幅图像所需数据量的技术与科学，且也是数字图像处理领域最成功的技术之一。在这一章我们将介绍数字图像压缩的理论和实践。将考察最常用的压缩技术，并且讲述有用的工业标准。

背景知识

数据压缩是指减少表示给定信息量所需数据量的处理。在这种定义中，数据和信息是不相同的事情，数据是信息传递的手段，相同数据的信息可以由不同数量的数据表示，包含不相关或重复信息的表示就被称为冗余数据 。

8.1基础知识

术语数据压缩是指减少表示给定信息量所需数据量的处理。在数字图像压缩中通常是二维灰度值阵列表示一幅图像所需的比特数。并且二维灰度列阵受可被识别和利用的三种类型的影响可以分为，第一编码冗余，第二是空间和时间冗余，第三是不相关的信息。

空间冗余

同一景物表面上采样点的颜色之间通常存在着空间关联性，相邻各点的取值往往近似或者相同，这就是空间冗余。

在图中计算机生成的恒定灰度线的集合，在对应的二维灰度阵列中：

 1.所有256种灰度都是等概率的，图像的直方图是均匀的。
 
 2. 因为每条线的灰度是随机选择的，在垂直方向上，每条线的像素彼此是独立的。
 
 3.因为沿每条线的像素是相同的，因此在水平方向上它们是最大相关的(完全互相依赖)

编码冗余

在之前，我们在图像的灰度值为随机变量的假设基础上，探讨了通过直方图处理进行图像增强技术。同样，我们也将利用类似的表示方法介绍最佳信息编码。
区间[0,L-1]内的一个离散随机变量r_{k}表示为一幅M*N大小图像的灰度，则每个r_{k}发生的概率为：

L是灰度级数，n_{k} 是第k级灰度在图像中出现的次数，若用于表示每个r_{k}值的比特数为l(r_{k}),则表示每个像素所需的平均比特数为：

时间冗余

时间冗余主要发生在视频中。视频一般为位于一时间轴区间的一组连续画面，其中的相邻帧往往包含相同的背景和移动物体，只不过移动物体所在的空间位置略有不同，所以后一帧的数据与前一帧的数据有许多共同的地方，这种共同性是由于相邻帧记录了相邻时刻的同一场景画面，所以称为时间冗余。

如上图所示，例如1秒25帧，每一帧之间都是间隔很短，前后帧的变话很少，也许物体只有细微的变化，主题背景不会发生改变。（前后两帧几乎没变化）

8.2一些基本的压缩方法

霍夫曼编码

消除编码冗余的一种最常用技术要归功于霍夫曼。当单独的对信源的符号进行编码，霍夫曼编码对每个信源符号产生了可能最小数量的编码符号。进行编码步骤大致可以如下
1.将信源符号的概率按减小的顺序排队。
2.把两个最小概率相加，并继续这一步骤，始终将较高的概率分支放在右边，直到最后变成概率１。
3.画出由概率１处到每个信源符号的路径，顺序记下沿路径０和１，所得就是该符号的霍夫曼码字。
4.将每对组合的左边一个指定为0，右边一个指定为1（或相反）。

可以通过代码部分来实现霍夫曼编码

import queue
class Node:
    def __init__(self, x, k=-1, l=None, r=None, c=''):
        self.freq = x
        self.key = k
        self.left = l
        self.right = r
        self.code = c
    def __lt__(self, otr):
        return self.freq < otr.freq
def huffman_code(data):
    freqTable = {}
    nodeList = []
    que = queue.PriorityQueue()
    codeTable = {}
    for n in data:
        if n in freqTable:
            freqTable[n] += 1
        else:
            freqTable[n] = 1
    for k, v in freqTable.items():
        nodeList.append(Node(v, k))
        que.put(nodeList[-1])
    while que.qsize() > 1:
        n1 = que.get()
        n2 = que.get()
        n1.code = '1'
        n2.code = '0'
        nn = Node(n1.freq + n2.freq, l=n1, r=n2);
        nodeList.append(nn);
        que.put(nodeList[-1])
    def bl(p, codestr=[]):
        codestr.append(p.code)
        if p.left:
            bl(p.left, codestr.copy())
            bl(p.right, codestr.copy())
        else:
            codeTable[p.key] = ''.join(codestr)
    bl(nodeList[-1])
    print(str(codeTable))
    return codeTable
if __name__ == '__main__':
    data = [1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5]
    huffman_code(data)

我们可以观察实验霍夫曼编码过程

算数编码

不同于前两节的变长编码，算术编码生成的是非块码。信源符号与码字之间不存在一一对应的关系，反而是给信源符号的整个序列分配了一个单元的算术码字。算术编码的基本原理是将编码的消息表示成实数0和1之间的一个间隔，消息越长，编码表示它的间隔就越小，表示这一间隔所需的二进制位就越多。

使用自适应上下文相关的概率估计

图上给出了二值信源符号的自适应上下文相关算术编码步骤。

行程编码

行程编码就是为了解决上述所提到的空间冗余，也称RLE。也就是在一幅图像中具有许多颜色相同的图块，在这些图块中，许多行上都具有相同的颜色，或者在一行上有许多连续的像素都具有相同的颜色值。在这种情况下就不需要存储每一个像素的颜色值，而仅仅存储一个像素的颜色值，以及具有相同颜色的像素数目就可以，或者存储像素的颜色值，以及具有相同颜色值的行数。

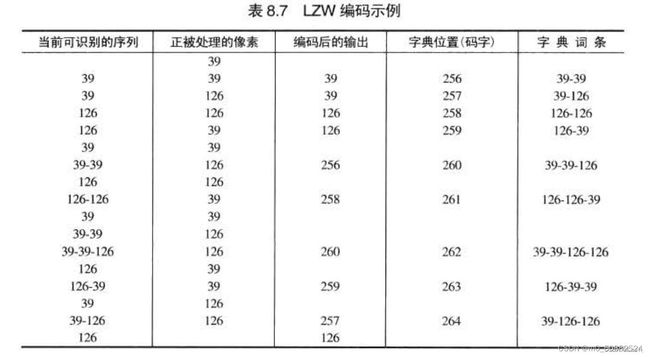
用行程编码来实现图像压缩，代码结果如下

import cv2 as cv
import numpy as np

##彩色图像灰度化
image = cv.imread('',1)
grayimg = cv.cvtColor(image, cv.COLOR_BGR2GRAY)
rows, cols = grayimg.shape

image1 = grayimg.flatten() #把灰度化后的二维图像降维为一维列表
#print(len(image1))

#二值化操作
for i in range(len(image1)):
    if image1[i] >= 127:
        image1[i] = 255
    if image1[i] < 127:
        image1[i] = 0

data = []
image3 = []
count = 1
#行程压缩编码
for i in range(len(image1)-1):
    if (count == 1):
        image3.append(image1[i])
    if image1[i] == image1[i+1]:
        count = count + 1
        if i == len(image1) - 2:
            image3.append(image1[i])
            data.append(count)
    else:
        data.append(count)
        count = 1

if(image1[len(image1)-1] != image1[-1]):
    image3.append(image1[len(image1)-1])
    data.append(1)

#压缩率
ys_rate = len(image3)/len(image1)*100
print('压缩率为' + str(ys_rate) + '%')

#行程编码解码
rec_image = []
for i in range(len(data)):
    for j in range(data[i]):
        rec_image.append(image3[i])

rec_image = np.reshape(rec_image,(rows,cols))

#cv.imwrite('image/output.jpg',rec_image)
cv.imwrite('image/output_fruit.jpg',rec_image)
cv.imshow('rec_image',rec_image) #重新输出二值化图像
cv.waitKey(0)

原图如上，压缩之后的图像如下所示

分析：从实验结果可以看出经过压缩之后的图像主体轮廓还是存在的，但是缺少细节的描述且此次压缩率为2.832%

JPEG编码

使用最为普通且广泛的连续色调静止帧压缩标准是JPEG标准。它定义了三种不同的编码系统：
    1、一种有损的基本编码系统，该系统以DCT为基础，并且适用于大多数压缩；
    2、一种扩展的编码系统，它面向更大压缩、更高精度或渐进的重建应用；
    3、一种面向可逆压缩的无损独立编码系统。
    压缩本身按三个顺序步骤执行：DCT计算、量化和变长码分配。
    JPEG是一种很灵活的格式，具有调节图像质量的功能，它允许用不同的压缩比例对文件进行压缩，支持多种压缩级别，压缩比率通常在10；1到40；1，压缩比越大，图像品质就越低；相反地，压缩比越小，图像品质就越高。

块变换编码

这项技术可以将图像分成大小相等且不重叠的小块，并使用二维变换单独地处理这些块。在块变换编码中，用一种可逆线性变换将每个块或子图像映射为变换系数集合，之后对这些变换系数进行量化和编码。

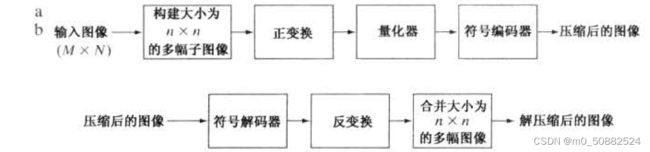
上图为块变换编码系统，解码器执行(除了量化功能外)与编码器相反顺序的步骤。编码器执行4种相对简单的操作:子图像分解、变换、量化和编码。一幅大小为M×N的输人图像首先被分解为大小为n×n的子图像，然后变换这些子图以生成MNIn2个子图像变换阵列，每个阵列的大小为n×n。变换处理的目的是对每幅子图像中的像素进行去相关，或用最少数量的变换系数包含尽可能多的信息。然后，在量化阶段，以一种预定义的方式有选择性地消除或更粗略地量化那些携带最少信息的系数。这些系数对重建的子图像质量的影响最小。通过对量化后的系数进行编码来结束编码过程。

比特平面编码

先前提及的编码技术多用于处理多于两级灰度的图像，比特平面编码基于如下技术：把一幅多级图像分解位一系列二值图像，并使用几种熟知的二值压缩方法之一来压缩每幅二值图像。一幅m比特单色图像的灰度可以表示为：

基于这种特性，可以将该图像分解为二值图像集的一种简单方法是把该多项式的m个系数分离为m个1比特的比特平面。一般来讲，每个比特平面都由给其像素置一个来自原始图像每一像素的合适的比特值或多项式系数来重建。例如，一个灰度为127（二进制为：01111111）的像素与一个灰度为128（二进制：10000000）的像素相邻，每个比特平面将包含一个对应0到1的转换。

下面用代码实现比特平面编码，展示结果（实验代码参考链接：http://t.csdn.cn/NsTAE）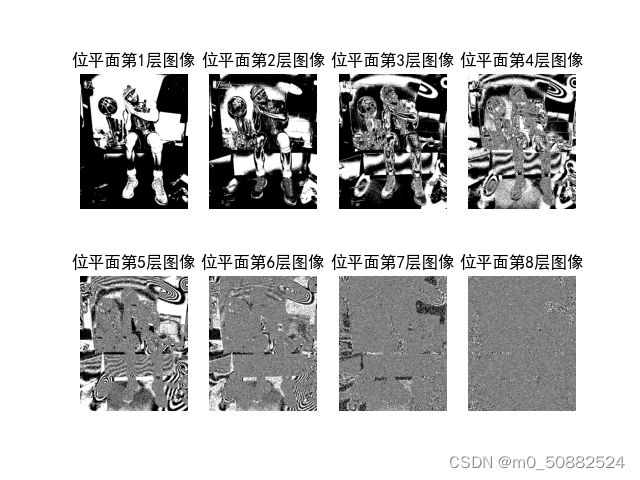

分析：从实验结果可以看出低平面比高平面的细节展示要更多；

8.3数字图像水印

图像在数字媒体和互联网中实际散步，并且这样散步的图像可以被重复并且无误的复制。所以防止非法复制的方法之一就是把水印的一条或者多条信息插入图像。
数字水印是将特定的数字信号嵌入数字产品中保护数字产品版权或完整性的技术。
简单的可见水印是一幅不透明或者半透明的子图像或者是放在另外一幅图像之上。

简单可见水印由如下公式生成：

F=（1+α）f+αw
α控制水印衬底的相对可见性，f为衬底，w为水印图片。通常α取值为0-1之间，效果如下所示，可以调节α的值来增强水印的效果
代码部分

import cv2
import matplotlib.pyplot as plt
import numpy as np 
img = cv2.imread("  ")# 原图
img = img[:, :, [2, 1, 0]]
img_water = cv2.imread("  ")# 添加的水印
img_water = img_water[:, :, [2, 1, 0]]

img_ = img.copy()
for x in range(img_water.shape[0]):
     for y in range(img_water.shape[1]):
         img_[x][y][0:3] = 0.3 * img_[x][y][0:3] + 0.7 * img_water[x][y][0:3]
        
plt.figure(dpi = 120)

plt.subplot(121)
plt.imshow(img)
plt.title("Origin picture")

plt.subplot(122)
plt.imshow(img_)
plt.title("Digital Watermark(α=0.7)")

plt.tight_layout()
plt.show()