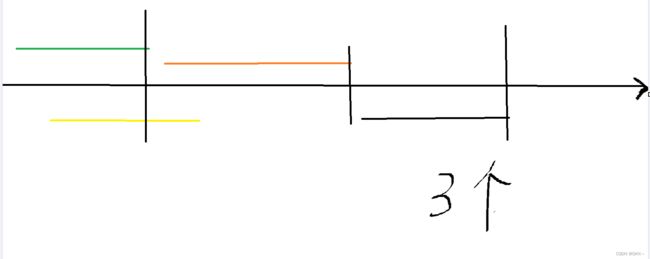贪心(5)
绝对值不等式 |x-a|+|x-b|>=|a-b| (中位数)
仓库选址(中位数就是最优解)
在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式
第一行输入整数 N。
第二行 N 个整数 A1∼AN
输出格式
输出一个整数,表示距离之和的最小值。
数据范围
1≤N≤100000
0≤Ai≤40000
输入样例:
4
6 2 9 1
输出样例:
12
#include
#include
using namespace std;
const int N=1e5+10;
int a[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n);
int res=a[n/2+1];
int num=0;
for(int i=1;i<=n;i++)
{
num+=abs(res-a[i]);
}
cout< 排序不等式
排队打水
(按照从小到大排序,等待时间之和最小)
有 n 个人排队到 1 个水龙头处打水,第 i 个人装满水桶所需的时间是 ti,请问如何安排他们的打水顺序才能使所有人的等待时间之和最小?
输入格式
第一行包含整数 n。
第二行包含 n 个整数,其中第 i 个整数表示第 i 个人装满水桶所花费的时间 ti。
输出格式
输出一个整数,表示最小的等待时间之和。
数据范围
1≤n≤10^5
1≤ti≤10^4
输入样例:
7
3 6 1 4 2 5 7
输出样例:
56#include
#include
using namespace std;
const int N=1e5+10;
int a[N];
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n);
long long sum=0;
for(int i=1;i<=n;i++)
{
sum+=a[i]*(n-i);//a[i]*后面还有多少人需要等这个人
}
cout< Huffman树
合并果子
在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并,达达可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过 n−1次合并之后,就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为 1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使达达耗费的体力最少,并输出这个最小的体力耗费值。
例如有 3 种果子,数目依次为 1,2,9。
可以先将 1、2 堆合并,新堆数目为 3,耗费体力为 3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12,耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。
输入格式
输入包括两行,第一行是一个整数 n,表示果子的种类数。
第二行包含 n 个整数,用空格分隔,第 i 个整数 ai 是第 i 种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。
输入数据保证这个值小于 231。
数据范围
1≤n≤10000
1≤ai≤20000
输入样例:
3
1 2 9
输出样例:
15#include
#include
#include
using namespace std;
int main()
{
priority_queue,greater>heap;
int n;cin>>n;
for(int i=1;i<=n;i++)
{
int a;cin>>a;
heap.push(a);
}
int ans=0;
while(heap.size()>1)
{
int x1=heap.top();
heap.pop();
int x2=heap.top();
heap.pop();
ans+=x1+x2;
heap.push(x1+x2);
}
cout< 区间问题
左端点排序或者右端点排序
考虑有一些活动是我们可以参加的 每个活动都有其开始时间和结束时间 我们可以将每个活动按照结束时间进行排序 可以发现 选择早结束的活动和选择晚结束的活动 对最后的答案贡献都是1 但是如果选择了结束时间早一些的活动 那么就可以给之后预留出更多时间 从而产生好的结果
区间选点
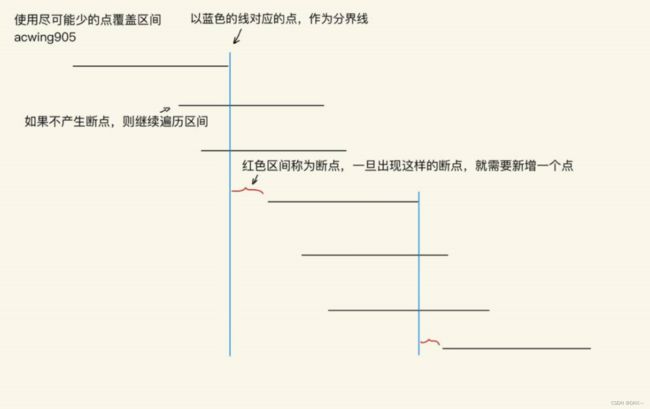
可以按前一题的方式将所有区间分为几个集合,每个集合中各个区间都至少有一点相交。若要选取不相交两个区间,那么两个区间必定处于不同的集合中,而最大的不相交区间数量便是总集合数,也就是区间选点的数量。所以两题代码相同。
给定 N个闭区间 [ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需的点的最小数量。
数据范围
1≤N≤10^5
−10^9≤ai≤bi≤10^9
输入样例:
3
-1 1
2 4
3 5
输出样例:
2#include
#include
using namespace std;
const int N=102000;
struct ss
{
int l,r;
}stu[N];
int cmp(ss x,ss y)
{
return x.r>n;
for(int i=0;i>stu[i].l>>stu[i].r;
sort(stu,stu+n,cmp);
int ans=0;
int num=-2e9;
//或者可以 ans=1,num=stu[1].r;
for(int i=0;inum)
{
num=stu[i].r;
ans++;
}
}
cout< 最大不相交区间数量
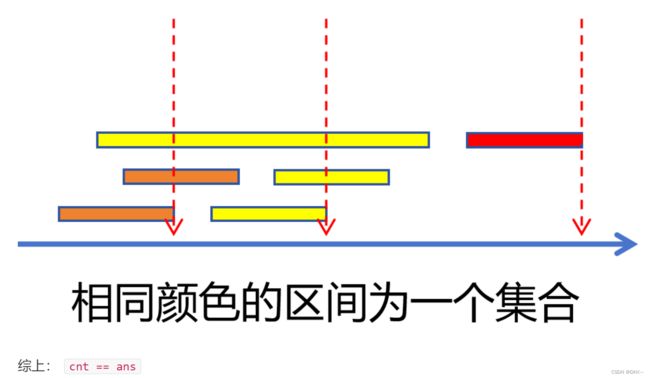
区间选点就是要选一个多区间重合的地方。题目中要求选不相交的区间,那么当几个区间重合时就只能取其中一个,就刚好与选区间重合之处相同。
可以按前一题的方式将所有区间分为几个集合,每个集合中各个区间都至少有一点相交。若要选取不相交两个区间,那么两个区间必定处于不同的集合中,而最大的不相交区间数量便是总集合数,也就是区间选点的数量。所以两题代码相同。
给定 N 个闭区间 [ai,bi],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。
输出可选取区间的最大数量。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示可选取区间的最大数量。
数据范围
1≤N≤10^5
−10^9≤ai≤bi≤10^9
输入样例:
3
-1 1
2 4
3 5
输出样例:
2#include
#include
using namespace std;
const int N=1e5+10;
struct ss
{
int l,r;
}stu[N];
int cmp(ss x,ss y)
{
return x.r>n;
for(int i=1;i<=n;i++) cin>>stu[i].l>>stu[i].r;
sort(stu+1,stu+1+n,cmp);
int ans=0;
int num=-2e9;
for(int i=1;i<=n;i++)
{
if(stu[i].l>num)
{
ans++;
num=stu[i].r;
}
}
cout< #include
#include
using namespace std;
const int N=1e5+10;
struct ss
{
int l,r;
}stu[N];
int cmp(ss x,ss y)
{
return x.r>n;
for(int i=1;i<=n;i++) cin>>stu[i].l>>stu[i].r;
sort(stu+1,stu+1+n,cmp);
int ans=1;
int num=stu[1].r;
for(int i=2;i<=n;i++)
{
if(stu[i].l>num)
{
ans++;
num=stu[i].r;
}
}
cout< 按照左端点进行从小到大排序
相交的区间选择 ed=右端最小的那个 (相当于结束最早) 这样可以选择更多的左端>ed
#include
#include
using namespace std;
const int N=1e5+10;
struct ss
{
int l,r;
}stu[N];
int cmp(ss x,ss y)
{
return x.l>n;
for(int i=1;i<=n;i++) cin>>stu[i].l>>stu[i].r;
sort(stu+1,stu+1+n,cmp);
int ans=1;
int ed=stu[1].r;
for(int i=2;i<=n;i++)
{
if(stu[i].l>ed)
{
ans++;
ed=stu[i].r;
}
else ed=min(stu[i].r,ed);
}
cout< 转换问题角度
最大的不相交区间数量
最小的相交区间数量
选择最多的点使得每个区间至少包含一个
因为上面一题是求最少的点使得每个区间都至少包含即变相的保证了最多的相交区间
因为我们反向考虑则最少的相交区间就是最多的点
因此我们只需要在上面那题,当两个区间相交的时候计算一下答案即可
最后输出n−res
区间分组
给定 N 个闭区间 [ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示最小组数。
数据范围
1≤N≤10^5
−10^9≤ai≤bi≤10^9
输入样例:
3
-1 1
2 4
3 5
输出样例:
2