数据结构之队列（源代码➕图解➕习题）

前言

        在学过栈之后，会了解到栈的底层是根据顺序表或者链表来构建的，那么我们今天要学习的队列是否也是基于顺序表和链表呢？那我们直接进入正题吧！

1. 队列的概念（图解）

        还是跟上节一样，依旧用图解的方式让大家更好的理解概念。

1.1 队列的组成：

        队列：队列指的是图中黑色边框及其内部的空间

        队头：出元素的一边叫队头

        队尾：入元素的一边叫队尾

        队内元素：蓝色正方形

1.2 队列的进出规则：先进先出

        队列的进出规则跟栈不一样，栈是先进后出，而队列是先进先出。

        队列只能从队头出，队尾入，所以这就造就了队列的先进先出，先从队尾入的元素，先从队头出。

2. 队列的架构

2.1 队列为顺序表构成（舍弃方案）

        队列的入队列相当于尾插（头插），队列的出队列相当于头删（尾删）        

        我们知道顺序表的尾插尾删是非常快的，很方便。但是头插头删却需要挪动数据，覆盖，十分麻烦。无论是我们入队列和出队列，我们都必然会涉及到头的挪动。这样大大增加了我们时间复杂度，所以我们队列不推荐使用顺序表构建。

2.2 队列为链表构成（文末源代码）

        我们是选择什么样的链表呢？单向链表还是双向链表，是否带头，是否成环？不要着急，我们先来看单链表是否简单可行。

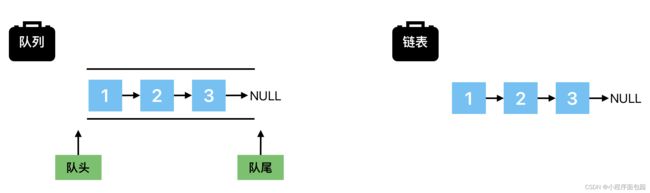
2.2.1 队列为单链表构成

        如图，我们选择链表的头部作为了队头，链表的尾部作为了队尾，那么出队列就是头删，入队列就是尾插。

1. 入队列：

        入队列就是链表的尾插，先找到链表的尾，再跟新节点连接就可以了。但是当我们队列中没有元素的时候，就需要改变一下链表头指针指向的位置，让他指向第一个节点，这里我们是改变指针，需要用到二级指针，但是我们今天不用二级指针，使用一个新的方法来解决。

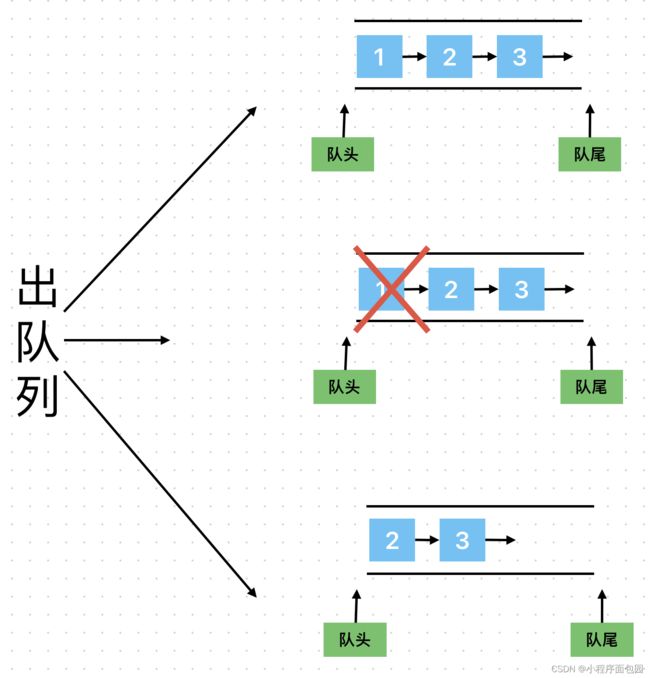
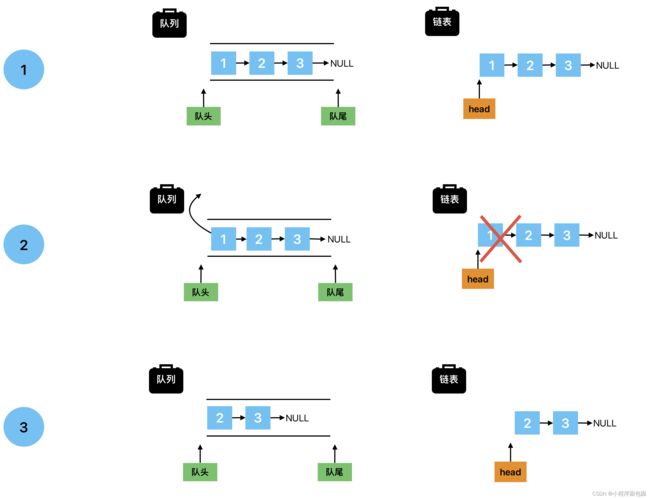
2. 出队列

        出队列相当于链表的头删，看图就可以了。        

我们会发现其实单链表已经可以几乎很好的解决队列这个数据结构了，那我们就没有必要去创造什么带头啊，循环啊，双向啊这些结构。所以接下来就让源代码登场吧！

3. 队列由单链表构成（源代码）

3.1 队列的定义

        这里跟以往不同的点是 这里我们重新定义了一个结构体，包含了队列的头节点和尾结点，我们这么定义的目的是可以更改头节点和尾节点。

//如果你要更改队列元素的数据类型，在这里更改一次就OK了，int变成其他数据类型
typedef int QDataType; 
//这里我们正常定义队列的节点，因为是链表构成的，和链表节点一样
typedef struct QueueNode 
{
    struct QueueNode* next;
    QDataType data;
}QNode;
//这里我们重新定义了一个结构体，包含了队列的头节点和尾结点，我们这么定义的目的是可以更改头节点和尾节点
typedef struct Queue
{
    QNode* head;
    QNode* tail;
    int size;
}Que;

3.2 队列的初始化

//初始化
void QueueInit(Que* pq)
{
    assert(pq);

    pq->head = pq->tail = NULL;
    pq->size = 0;
}

3.3 队列的销毁

void QueueDestroy(Que* pq)
{
    assert(pq);

    QNode* cur = pq->head;
    while (cur)
    {
        QNode* next = cur->next;
        free(cur);
        cur = next;
    }

    pq->head = pq->tail = NULL;
    pq->size = 0;
}

3.4 入队列

//入队列
void QueuePush(Que* pq, QDataType x)
{
    assert(pq);

    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    if (newnode == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }

    newnode->data = x;
    newnode->next = NULL;

    if (pq->tail == NULL)
    {
        pq->head = pq->tail = newnode;
    }
    else
    {
        pq->tail->next = newnode;
        pq->tail = newnode;
    }

    pq->size++;
}

3.5 出队列

//出队列
void QueuePop(Que* pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));

    if (pq->head->next == NULL)
    {
        free(pq->head);
        pq->head = pq->tail = NULL;
    }
    else
    {
        QNode* next = pq->head->next;
        free(pq->head);
        pq->head = next;
    }

    pq->size--;
}

3.6 取队头元素

//取队头元素
QDataType QueueFront(Que* pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));

    return pq->head->data;
}

3.7 取队尾元素

//取队尾元素
QDataType QueueBack(Que* pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));

    return pq->tail->data;
}

3.8 判断队列是否为空

bool QueueEmpty(Que* pq)
{
    assert(pq);

    return pq->head == NULL;
}

3.9 求队列长度

//队列的长度
int QueueSize(Que* pq)
{
    assert(pq);

    return pq->size;
}

4. 习题

4.1 下列关于队列的叙述错误的是（ ）

A.队列可以使用链表实现

B.队列是一种“先入先出”的数据结构

C.数据出队列时一定只影响尾指针

D.数据入队列时一定从尾部插入

答案：C

解析：出队操作，一定会影响头指针，如果出队之后，队列为空，会影响尾指针。

4.2  用无头单链表存储队列，其头指针指向队头结点，尾指针指向队尾结点，则在进行出队操作时（）

A.仅修改队头指针

B.队头、队尾指针都要修改

C.队头、队尾指针都可能要修改

D.仅修改队尾指针

答案：C

解析：出队操作，一定会修改头指针，如果出队之后，队列为空，需要修改尾指针。

4.3 以下不是队列的基本运算的是（ ）

A.从队尾插入一个新元素

B.从队列中删除队尾元素

C.判断一个队列是否为空

D.读取队头元素的值

答案：B

解析：队列只能从队头删除元素。

4.4 下面关于栈和队列的说法中错误的是（ ）（多选）

A.队列和栈通常都使用链表实现

B.队列和栈都只能从两端插入、删除数据

C.队列和栈都不支持随机访问和随机插入

D.队列是“先入先出”，栈是“先入后出”

答案：AB

解析：

A错误：栈是尾部插入和删除，一般使用顺序表实现，队列是头部删除尾部插入，一般使用链表实现

B错误：栈是后进先出，尾部插入和删除，并不是两端；队列是先进先出，尾部插入头部删除。

4.5 下列关于顺序结构实现循环队列的说法，正确的是（ ）

A.循环队列的长度通常都不固定

B.直接用队头和队尾在同一个位置可以判断循环队列是否为满

C.通过设置计数的方式可以判断队列空或者满

D.循环队列是一种非线性数据结构

答案：C

解析：顺序结构实现循环队列是通过数组下标的循环来实现的

A错误：循环队列的长度都是固定的

B错误：队头和队尾在同一个位置时 队列可能是空的，也可能是满的，因此无法判断

C正确：设置计数即添加一个字段来记录队列中有效元素的个数，如果队列中有效元素个数等于空间总大小时队列满，如果队列中有效元素个数为0时队列空

D错误：循环队列也是队列的一种，是一种特殊的线性数据结构

好啦，我们关于队列的实现已经结束了，谢谢大家！