高精度加减乘除——C++实现

每日一句：每天早上醒来时，我们有两个简单的选择：回头去睡，继续做梦。或者起身去追逐梦想。

---

前言

学高精度加减乘除有什么用呢？当你要算的加减法没有超出数据类型最大的long long的范围时，当然不需要用到高精度，当你计算的数据过于大的时候呢？这个时候，就需要高精度算法了，利用**数字字符-‘0’**可以得到数字。

一、高精度加法

1.基本思路

高精度加法就是模拟小学学的加法操作，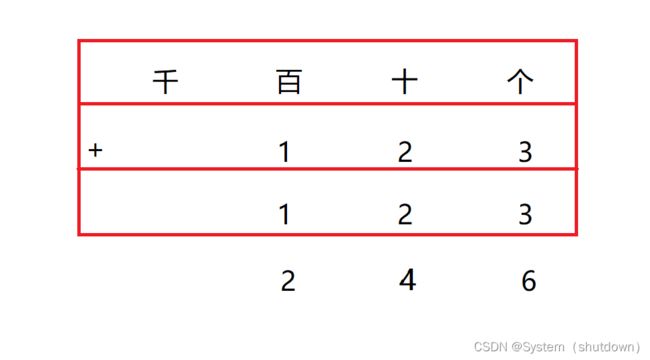
相信这个运算对大家来说是特别简单的，尽管有进位，那么，我们怎么用代码去实现呢？

2.分步讲解

2.1输入字符数字

	string a, b;
	vector<int>A, B;
	cin >> a >> b;

将长整数当成字符进行输入，那为什么不直接用数组存数字呢？当你给数组输入数字的时候，你需要一位一位的输入，利用字符可以直接输完，再用数组把数字存起来就可以了。

2.2把字符数字转换为数字

先把代码给出来

	string a, b;
	vector<int>A, B;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}

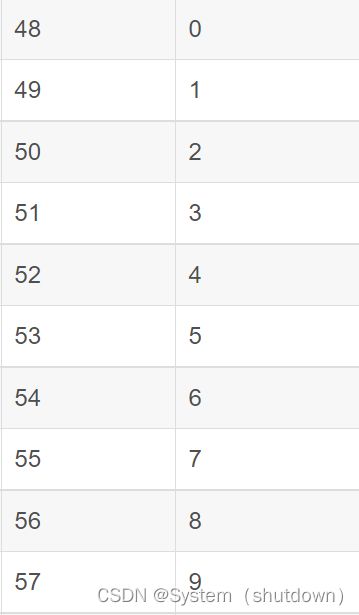
把字符1和字符0相减，差值刚好是1，这样就可以把1存进数组里，其他的数字也是这样的操作，为了把每位数都转换，可以利用for循环，但要注意，转换这一步是倒着存在数组里的，为什么呢？看下面的图，我们进行加减法的时候是说的一百二十三，如果不把数组倒着存，那么就会造成先把百位进行了加法，这样在进行有进位的计算时就会出现错误。

	for (int i = 0; i < a.size(); i++)
	{
		A.push_back(a[i] - '0');
	}
	for (int i = 0; i < b.size(); i++)
	{
		B.push_back(b[i] - '0');
	}

这样就会造成结果错误，当然个人觉得把代码改改，改成高位在前面的也不是不能写但会比较麻烦（没有尝试）各位可以自行测试一下。

2.3实现add函数

实现add函数，也是比较关键的一步，在这个函数里面，又定义了一个C和t（t表示的就是A[i]加B[i]之后的值），在这个C里面，存的就是答案，只不过要注意这个答案在C里面也是倒序的，在输出的时候，要注意取值问题。

	for (int i = 0; i < A.size() || i < B.size(); i++)
	{
		if (i < A.size())
		{
			t += A[i];
		}
		if (i < B.size())
		{
			t += B[i];
		}
		C.push_back(t % 10);
		t /= 10;
	}

这里要注意循环条件，一定要小于A的长度或者小于B的长度，满足二者之一即可，因为前面的代码中并没有专门去进行A,B长度的比较。比较一下也很简单。

if(A.size() < B.size())
{
	return add(B,A);	
}

这样写的话，下面的for循环的循环条件只需要小于A就行了。
但是这样考虑的情况并不完美，如果高位又进位了，怎么办？，在这个循环里面，并没有解决这个问题的步骤，注意：在加法中进位，最多进1位，所以，我们可以用if来判断t为真假就可以了。

	if (t)
	{
		C.push_back(t);
	}

这就是完整的高精度加法操作了。

3.完整代码

#include 
#include 
using namespace std;

vector<int> add(vector<int>& A, vector<int>& B)//这里的&是引用的意思，在这里不过多介绍
{
	int t = 0;
	vector<int> C;
	for (int i = 0; i < A.size() || i < B.size(); i++)
	{
		if (i < A.size())
		{
			t += A[i];
		}
		if (i < B.size())
		{
			t += B[i];
		}
		C.push_back(t % 10);
		t /= 10;
	}
	if (t)
	{
		C.push_back(t);
	}
	return C;
}

int main()
{
	string a, b;
	vector<int>A, B;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}

	auto C = add(A, B);

	for (int i = C.size() - 1; i >= 0; i--)
	{
		cout << C[i];
	}
	return 0;
}

例题详见acwing791.高精度加法

二、高精度减法

1.基本思路

高精度减法和高精度加法的思路其实都差不多，都是最基本的运算法则。

2.分步讲解

2.1~2.2

	string a, b;
	vector<int>A, B;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}

这个代码的思路跟高精度加法的思路是一样的，就不在细说了。

2.3cmp函数

要注意一个问题就是要相减的两个数，谁大，谁小，这个时候就要额外写一个用于比较大小的函数。这个函数能放止出现小数-大数的情况，就比如111 - 888，可以先进行888 - 111的运算，先输出-，在输出777，这样不也是-777。
代码

bool cmp(vector& A, vector& B)
{
	if (A.size() != B.size())
	{
		return A.size() > B.size();
	}

	for (int i = A.size() - 1; i >= 0; i--)
	{
		if (A[i] != B[i])
		{
			return A[i] > B[i];
		}
	}

	return true;
}

如果A的长度和B的长度是不相同，就可以直接利用A,B的长度去分辨谁大谁小，当A和B的长度相等的时候，就直接从数的最高位，也就是A,B的最后一个元素去进行比较，若全部符合，则返回true，走到最后一步的时候，也说明了两个数字是相等的。

2.4sub函数实现

vector<int> sub(vector<int>& A, vector<int>& B)
{
	int t = 0;
	vector<int> C;
	for (int i = 0; i < A.size(); i++)
	{
		t += A[i];
		if (i < B.size())
		{
			t -= B[i];
		}
		C.push_back((t + 10) % 10);
		if (t < 0)
		{
			t = -1;
		}
		else
		{
			t = 0;
		}
	}
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}
	return C;
}

在cmp函数里已经比较过大小，所以，在这个减法函数里，A就是最大的数字，直接利用i C.push_back((t + 10) % 10);
这一步为什么要让t+10，再去%10呢？，在减完之后，t万一是个负数呢？加10%10的结果是0，相当于t+一个0，即使t是负数，加了10也不会影响结果。t在这里也可以借位，如100 - 69：（0 + 10 - 9） % 10 = 1；结果也应该输出1.

		if (t < 0)
		{
			t = -1;
		}
		else
		{
			t = 0;
		}

看这里，t<0,t就等于-1，然后回到第一步，t += A[i];，这不就是借位的实现吗？

2.5去除前导零

	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}

去除前导零是放止出现下面图片里的情况

有前导零的情况就是，位数大于1位，最后一位（最后一位是高位）必须得是0。

3.完整代码

#include 
#include 
using namespace std;

bool cmp(vector<int>& A, vector<int>& B)
{
	if (A.size() != B.size())
	{
		return A.size() > B.size();
	}

	for (int i = A.size() - 1; i >= 0; i--)
	{
		if (A[i] != B[i])
		{
			return A[i] > B[i];
		}
	}

	return true;
}

vector<int> sub_(vector<int>& A, vector<int>& B)
{
	int t = 0;
	vector<int> C;
	for (int i = 0; i < A.size(); i++)
	{
		t += A[i];
		if (i < B.size())
		{
			t -= B[i];
		}
		C.push_back((t) % 10);
		if (t < 0)
		{
			t = -1;
		}
		else
		{
			t = 0;
		}
	}
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}
	return C;
}

int main()
{
	string a, b;
	vector<int>A, B;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}
	if (cmp(A, B))
	{
		auto C = sub_(A, B);
		for (int i = C.size() - 1; i >= 0; i--)
		{
			cout << C[i];
		}
	}
	else
	{
		auto C = sub_(B, A);
		cout << "-";
		for (int i = C.size() - 1; i >= 0; i--)
		{
			cout << C[i];
		}
	}
	return 0;
}

例题详见acwing792.高精度减法

三、高精度乘法

1.基本思路

高精度乘法，用的还是最基本的运算思维，刚开始的思路跟加法差不多，先输入字符数字，然后转换为数字，进入mul函数，实现乘法操作，然后去除前导零。

2.分布讲解

2.1mul函数实现

前面思路和高精度加法思路差不多，详细看高精度加法2.1~2.2。

vector<int> mul(vector<int>& A, int& b)
{
	vector<int>C;
	int t = 0;
	for (int i = 0; i < A.size(); i++)
	{
		t += A[i] * b;
		C.push_back(t % 10);
		t /= 10;
	}
	if (t)
	{
		C.push_back(t);
	}
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}

	return C;
}

高精度乘法，在这里，用的是一个字符数字转化为数组，然后去乘一个int类型的数，没有用两个字符数字。
在这个函数里，只需要把A里面的每位数都b就能得到结果，中间的进位用t去表示，t%10，可以得到本位的数，t/10得到进位的数，然后在t += A[i] * b;这一步中，把进位的数字在加上去，直到循环结束，但别忘了，循环结束的时候，t可能还为真，这个时候就需要判断t是否为真，为真，就把t加在C的后面；为假则进行下一步。
去重，乘法为什么还要去重？因为会有012345的情况出现，这种情况不去重的话会出现00000的情况，所以要进行去重操作。

3.完整代码

#include 
#include 
using namespace std;

vector<int> mul(vector<int>& A, int& b)
{
	vector<int>C;
	int t = 0;
	for (int i = 0; i < A.size(); i++)
	{
		t += A[i] * b;
		C.push_back(t % 10);
		t /= 10;
	}
	if (t)
	{
		C.push_back(t);
	}
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}

	return C;
}

int main()
{
	string a;
	int b;
	vector<int>A;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}

	auto C = mul(A, b);

	for (int i = C.size() - 1; i >= 0; i--)
	{
		cout << C[i];
	}

	return 0;
}

详见例题acwing793.高精度乘法

四、高精度除法

1.基本思想

利用字符数字转化为数字，转化的同时把数字倒着存进数组A里，让A里的数去除要除的数，结果存在数组C里，然后把C输出。

2.分步讲解

2.1输入操作

	string a;
	int r ;//在这里，r表示的是余数
	int b;//b表示的是除数
	vector<int>A;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}

这个操作和高精度加法一样。

2.2div函数实现

	vector<int> C;
	for (int i = A.size() - 1; i >= 0; i--)
	{
		r =(r*10 + A[i]) ;
		C.push_back(r / b);
		r %= b;
	}
	reverse(C.begin(), C.end());
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}

因为对A的最高位开始处理，因为在前面把小位放在了A的前面，高位放在了后面，所以要i=A.size() - 1;

r =(r*10 + A[i]) ;

将上次的余数*10在加上当前位的数字，便是该位需要除的被除数，

C.push_back(r / b);

把商放在这里，

r %= b;

除完当前位的余数。

在除法操作中，是高位到低位的运算，所以C的前导零都在vector的前面，而vector是有pop_back()函数的，这个函数只能删除最后一位，所以要用reverse进行逆置，在进行去除前导零的操作。

	reverse(C.begin(), C.end());
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}

3.完整代码

#include 
#include 
#include 
using namespace std;

int r;

vector<int> div(vector<int>& A, int& b)
{
	vector<int> C;
	for (int i = A.size() - 1; i >= 0; i--)
	{
		r =(r*10 + A[i]) ;
		C.push_back(r / b);
		r %= b;
	}
	reverse(C.begin(), C.end());
	while (C.size() > 1 && C.back() == 0)
	{
		C.pop_back();
	}

	return C;
}

int main()
{
	string a;
	int b;
	vector<int>A;
	cin >> a >> b;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}
	auto C = div(A, b);

	for (int i = C.size() - 1; i >= 0; i--)
	{
		cout << C[i];
	}
	cout << endl << r;
	return 0;
}

详见例题acwing794.高精度除法
以上就是高精度加减乘除，希望对大家有帮助。