【人工智能】归结演绎推理

前言：在学习《人工智能》这门课程中的确定性定理这一章时，发现国内的大多数课本对于这一章的描述语言过于正式与抽象，有大量概念性的东西，不便于初学者理解，故本文从中学竞赛中的类似问题引入，深入浅出的介绍归结演绎推理的基本知识和应用，以供大家参考学习。

引文：如果读者在小学或中学时参过数学竞赛，肯定会记得在考场上看到了一道类似下题的推理题：

相信以诸位的聪明才智，不一会儿就能在纸上推出正确答案。在这里，其实引出了人工智能这门学科中很重要的一节内容：确定性推理。如果有读者的大学本科专业是计算机科学、人工智能，或者研究生是相关方向，则一定接触过此类知识。今天，我们就详细谈一谈这部分内容。

一、推理的基本概念


我们今天重点讨论的就是演绎推理。

假言三段论由古希腊著名思想家亚里士多德提出，具体见以下例子。

注：至于“推理”的其他概念，我就不多写了，以免概念性的东西写的太多，读者看多会烦躁，有兴趣可以参阅《人工智能》的相关书籍。

二、归结演绎推理
演绎推理分为自然演绎推理和归结演绎推理，我们重点来分析归结演绎推理，先上概念。


那么，何为鲁滨逊归结原理？

看上去很抽象，难以理解，我们来用一道非常经典的例题来说明。

已知：
（1）John是贼。
（2）Paul喜欢酒（wine）。
（3）Paul也喜欢奶酪（cheese）。
（4）如果Paul喜欢某物，那么John也喜欢某物。
（5）如果某人是贼，而且他喜欢某物，那么他就会偷窃该物。
请回答下面的问题：John会偷窃什么？

第一步：定义谓词。

thief(x)：某人x是贼；
like(x,y)：某人x喜欢某物y；
steal(x,y)：某人x偷窃某物y；

第二步：根据定义的谓词写出上述知识的谓词表示。

注：何为谓词表示？通俗点说就是利用单词或字母将题目所给的信息表达出来。

（1）John是贼。
谓词： thief(John)

（2）Paul喜欢酒（wine）。
谓词： like(Paul,wine)

（3）Paul也喜欢奶酪（cheese）。
谓词： like(Paul,cheese)

（4）如果Paul喜欢某物，那么John也喜欢某物。
谓词：($\forall$ y)(like(Paul,y)$\to$like(John,y))

（5）如果某人是贼，而且他喜欢某物，那么他就会偷窃该物。
谓词：($\forall$x) ($\forall$y)(thief(x) $\bigwedge$ like(x,y)$\to$steal(x,y))

这里补充一些连词和量词的知识：

第三步：化为字句集。

何为子句集？

所以，如果谓词表示中有合取（$\bigvee$）则不变；有析取（$\bigwedge$）则拆成两个字句集。并且：

将全称量词$\forall$去掉。

故原题字句集可化为：

S1={ thief(John)}

S2={ like(Paul,wine) }

S3={ like(Paul,cheese)}

S4={ ~like(Paul,y)∨ like(John,y)}

S5={ ~ thief(x) ∨~like(x,y) ∨steal(x,y)}

再将题目的问题“John会偷窃什么？”表示成谓词并且取反，与ANSWER做析取。
G：~steal(John,z) ∨ANSWER(z)

为什么要将题目的问题表示成谓词并取反呢，别着急，我们接着往下看。

第四步：使用归结原理对子句集进行归结。

何为“归结”，通俗理解就是“正反相消”，见下：

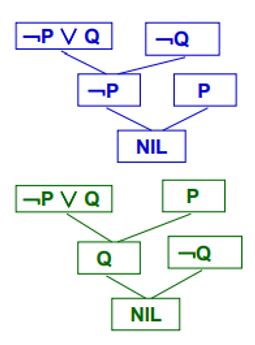
从图中可以发现：

所以可得：
(1)thief(John)
(2) like(Paul,wine)
(3) like(Paul,cheese)
(4) ~like(Paul,y)∨ like(John,y)
(5) ~ thief(x) ∨~like(x,y) ∨steal(x,y)
(6) ~steal(John,z) ∨ANSWER(z)

(7)~thief(John) ∨~like(John,z) ∨ANSWER(z)------------------------(5) (6)归结，{John/x, z/y}
(8) ~like(John,z) ∨ANSWER(z)------------------------------------------(1) (7)归结
(9) ~like(Paul,z)∨ANSWER(z)-------------------------------------------(4) (8)归结，{ z/y}
(10) ANSWER(wine) -------------------------------------------------------(2) (9)归结，{ wine/z}
(11) ANSWER(cheese)-----------------------------------------------------(3) (9)归结，{ cheese/z}

注：(1)到(6)为第三步得到的字句集，花括号里面的“/”表示“置换”。

以第(7)步为例分析：(5)和(6)归结，steal(x,y)与~steal(John,z) 相消，~ thief(x) ∨~like(x,y) 中的x和y分别换成 ~steal(John,z)中的John和z，所以就变为 ~thief(John) ∨~like(John,z) ∨ANSWER(z)，即第(7)步，其它同理。

所以，本题目有两个答案，John会偷窃wine，也会偷窃cheese。

看到这里我们就明白为什么要将题目的问题表示成谓词并取反，如果我们将结论取反后，即真变为假后，与已知证据最后相互抵消，那结论必为真。举个不太恰当的例子：就像一个未知数x（结论）取负数后为-x（结论取反），与1（证据）相加得0，则x必为1，即结论必为真。刚接触读者可能不甚理解，练几道推理题，多思考下，慢慢就可体会归结演绎推理其中的巧妙之处。

我再举题一例，读者可拿纸笔一同练习。

某单位招聘工作人员，张三、李四和王五三人应试，经面试后单位有如下想法：
（1）如果录取张三而不录取李四，则一定录取王五；
（2）如果录取李四，则一定录取王五；
（3）三人中一定要录取一人。
请用归结演绎方法求出：该单位一定录取谁？

读者可用归结演绎推理试做一下开头我引出的那道推理题。
（答案：C是老实人）

彩蛋：无意间发现站内有篇博文，详细的介绍了下归结演绎推理的基本知识，而且有我开头引出的那道题的解答过程，大家不妨一阅，作为本文的互补学习。博文地址：https://blog.csdn.net/wangran51/article/details/6906063

注明：本文章仅供学习参考之用。作者水平有限，不免有错漏之处，如有问题或建议，可留言告之。