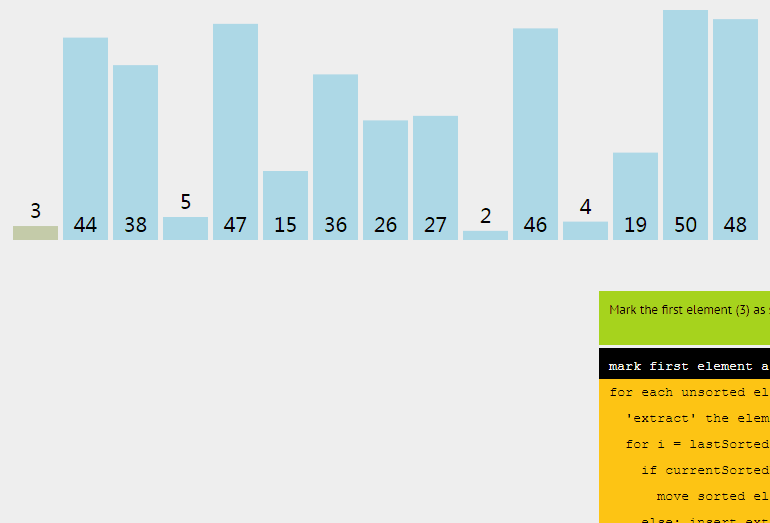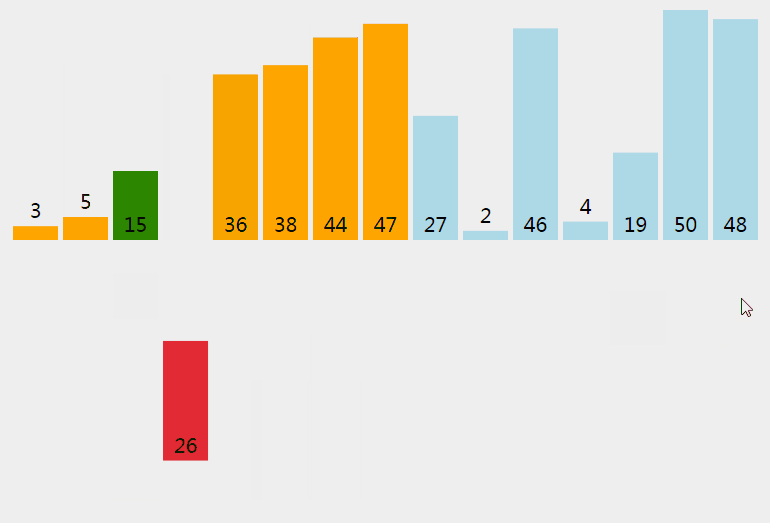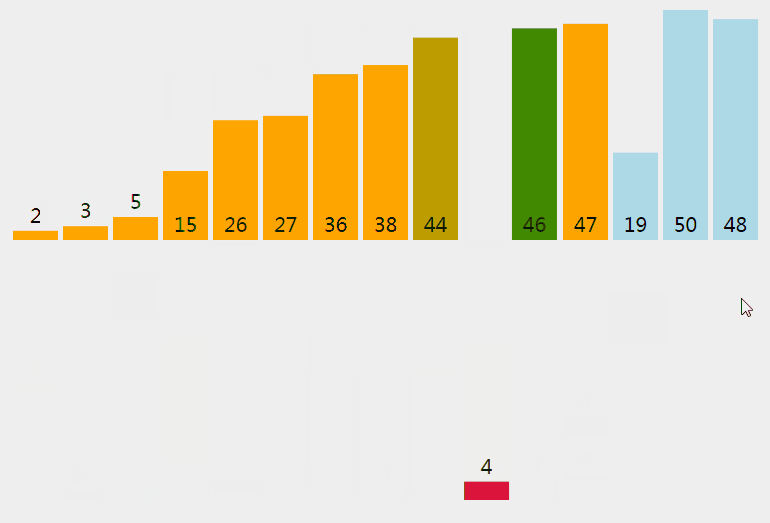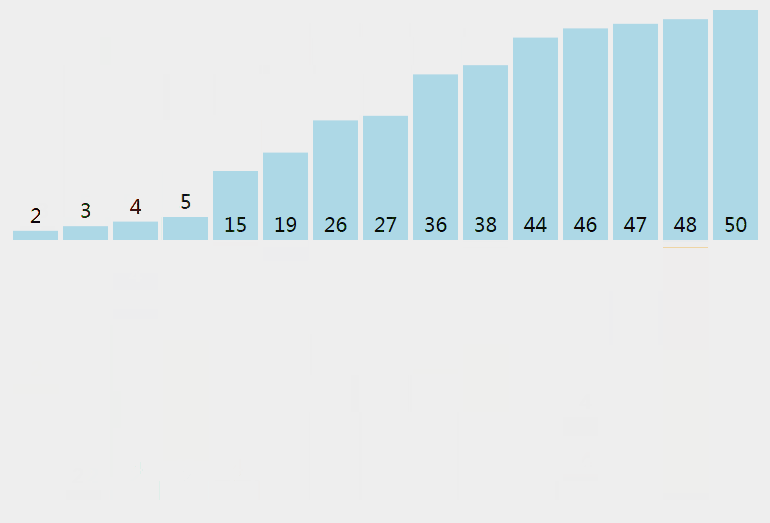
python排序算法的时间复杂度_常见排序算法及其对应的时间复杂度和空间复杂度...
排序算法经过长时间演变,大体可以分为两类:内排序和外排序。在排序过程中,全部记录存放在内存,则成为内排序;如果排序过程中需要使用外存,则称为外排序,本文讲的都属于内排序。
内排序有可以分为以下几类:
(1)插入排序:直接插入排序、二分法插入排序、希尔排序
(2)选择排序:直接选择排序、堆排序
(3)交换排序:冒泡排序、快速排序
(4)归并排序
(5)基数排序
排序方法
时间复杂度(平均)
时间复杂度(最坏)
时间复杂度(最好)
空间复杂度
稳定性
复杂性
直接插入排序
O(n2)
O(n2)
O(n)
O(1)
稳定
简单
希尔排序
O(nlog2n)
O(n2)
O(n1.3)
O(1)
不稳定
较复杂
直接选择排序
O(n2)
O(n2)
O(n2)
O(1)
不稳定
简单
堆排序
O(nlog2n)
O(nlog2n)
O(nlog2n)
O(1)
不稳定
较复杂
冒泡排序
O(n2)
O(n2)
O(n)
O(1)
稳定
简单
快速排序
O(nlog2n)
O(n2)
O(nlog2n)
O(nlog2n)
不稳定
较复杂
归并排序
O(nlog2n)
O(nlog2n)
O(nlog2n)
O(n)
稳定
较复杂
基数排序
O(d(n+r))
O(d(n+r))
O(d(n+r))
O(n+r)
稳定
较复杂
一、插入排序
•思想:每步将一个待排序的记录,按其顺序码大小插入到前面已经排序的字序列的合适位置,直到全部插入排序完为止。
•关键问题:在前面已经排好序的序列中找到合适的插入位置。
•方法:
直接插入排序
插入排序的最好情况是数组已经有序,此时只需要进行n-1次比较,时间复杂度为O(n)
最坏情况是数组逆序排序,此时需要进行n(n-1)/2次比较以及n-1次赋值操作(插入)
平均来说插入排序算法的复杂度为O(n2)
空间复杂度上,直接插入法是就地排序,空间复杂度为(O(1))
二分插入排序
最坏情况:每次都在有序序列的起始位置插入,则整个有序序列的元素需要后移,时间复杂度为O(n2)
最好情况:待排序数组本身就是正序的,每个元素所在位置即为它的插入位置,此时时间复杂度仅为比较时的时间复杂度,为O(log2n)
平均情况:O(n2)
空间复杂度上,二分插入也是就地排序,空间复杂度为(O(1))。
希尔排序
增量排序的时间复杂度依赖于所取增量序列的函数,但是到目前为止还没有一个最好的增量序列.有人在大量的实验后得出结论;当n在某个特定的范围后希尔排序的比较和移动次数减少至n^1.3 不管增量序列如何取值,都应该满足最后一个增量值为1。
有文献指出,当增量序列为d[k]=2^(t-k+1)时,希尔排序的时间复杂度为O(n^1.5), 其中t为排序趟数。
空间复杂度上,二分插入也是就地排序,空间复杂度为(O(1))。
1.直接插入排序
(1)基本思想:每步将一个待排序的记录,按其顺序码大小插入到前面已经排序的字序列的合适位置(从后向前找到合适位置后),直到全部插入排序完为止。(是一种最简单的排序方法,其基本操作是将一条记录插入到已排好的有序表中,从而得到一个新的、记录数量增1的有序表。)
(2)实例
(3)python实现
![]()
![]()
defInsertSort(list_):for i in range(1,len(list_)): #从列表的第二个元素开始找
j = i-1 #先定位第i个元素的前一个元素
if list_[j] > list_[i]: #如果前一个元素比第i个元素大
temp = list_[i] #前一个元素比i元素大,所以i元素需要往前插入,故先把list_[i]赋值给一个临时变量
list_[j+1] = list_[j] #i元素插入后,其前一个元素即j元素肯定向后位移一位
#继续往前寻找,如果有比临时变量大的数字,则后移一位,直到找到比临时变量小的元素或者达到列表第一个元素
j -= 1
while j >= 0 and list_[j] >temp:
list_[j+1] =list_[j]
j-= 1list_[j+