代码训练营第二天|数组part2|leetcode 977 有序数字的平方|leetcode 209 长度最小的子数组|leetcode 59 螺旋矩阵2
今日理论文章:数组总结
leetcode 977 有序数字的平方:leetcode 977
文章讲解:双指针理解
leetcode 209 长度最小的子数组:leetcode 209
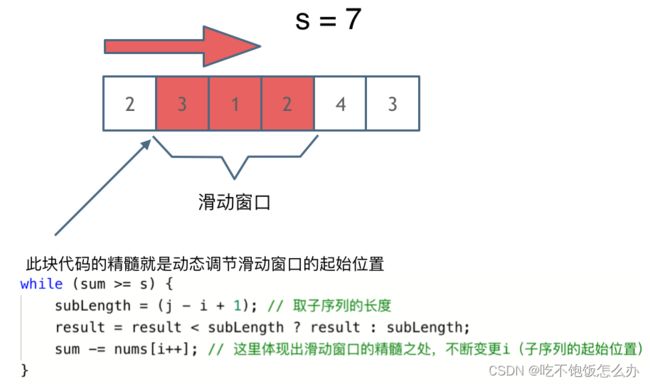
文章讲解:滑动窗口思路
leetcode 59 螺旋矩阵2:leetcode 59
文章讲解:嗯写就完了
目录
双指针:leetcode 977
1,根据题意,先跑一遍:
2,双指针做法
3,双指针代码:
4,更严谨的改进:
5,反思:
找规律:leetcode 209
1,题目分析:
2,滑动窗口:针对子序列的操作
痛苦面具de模拟:leetcode59 螺旋矩阵2⃣️
今日总结:
双指针:leetcode 977
1,根据题意,先跑一遍:
class Solution {
public:
vector sortedSquares(vector& nums) {
for(int&i:nums){
i = i*i;
}
sort(nums.begin(),nums.end());
return nums;
}
}; 平均时间复杂度O(n+nlogn),通过,但确实想不到时间复杂东O(n)的做法
2,双指针做法
看到之后,恍然大悟:
1,题目提供的非递减数组,无非就是三种情况:
[1,2,3,4,5] 这样的数组扫一遍就可以,
[-5,-4,-3,-2,-1]这样的数组扫一遍倒着存就可以
[-2,-1,0,1,2] 对于这个数组没有想到好的解决方法
而双指针的做法发掘了一个关键信息:数组非递减,隐藏信息就是,
(1)平方的最大值一定在数组的两侧
(2)在去掉两端的任意一个后,新数组仍然是非递减的,即新数组的平方最大值仍然在两端
思路就是:每次找数字最大值,一个一个存下来,而找最大值,只要比较每次两端的数,把大的那个存下来,指针向内侧移动就可以。
3,双指针代码:
class Solution {
public:
vector sortedSquares(vector& nums) {
int left = 0;
int right = nums.size()-1;
vector result(nums.size());
int index = right;
while(left<=right){
int lsquare = nums[left]*nums[left];
int rsquare = nums[right]*nums[right];
if(lsquare 时间复杂的O(n)
4,更严谨的改进:
在卡哥的示范代码中:
vector result(A.size(), 0); 给数组显式的指定初始值明显是更严谨的写法。
5,反思:
写代码题不是套模版,不能看到有人说双指针就想着一前一后的双指针去做。要拿出更严谨的态度,认真的分析题目给到的信息和提示找到隐藏的规律,再去选择使用什么方法,这是水到渠成的过程。
找规律:leetcode 209
1,题目分析:
首先看到,题目的正整数条件:target, nums, 在做完上面那道题后,这道题就有了思路:
1,首先,两个指针指向第一个数字,检查是否大于等于target,如果是,就返回1
2,如果是小于target的,那么由于nums中元素都是正的,那么让right后移,用sum去计算left和right之间的元素的和,此时又有两种情况:
3,如果还是小,就让right再往后移动,直到移动到最后或者找到sum大于等于target的点
4,如果已经大了,就去尝试减去前一个值,让left前移,如果移动后变小了,那么移动前的就是一个备选答案,如果移动后还是大于等于target,意思着left还可以向前移动
思路其实没有完全顺下来,但是可以试试写一下
class Solution {
public:
int minSubArrayLen(int target, vector& nums) {
int right = 0;
int left = 0;
int sum = 0;
int length = nums.size()+1;//记录最小长度,因此需初始化一个不可能的长度
while(right= target){//试着剪去前一个
length = min(length, right-left+1);//更新一下最小的长度
sum = sum - nums[left++];
}
right++;//right 往前走
}
if(length>nums.size())return 0;
else return length;
}
}; 通过
2,滑动窗口:针对子序列的操作
其实仔细理解一下,滑动窗口的目的是操作一个可变长的一个子序列,在我的做法中,看似是从双指针的角度分析的,但其实在代码中,我的sum和双指针的移动的目的都是操作nums数组中一个动态变化的序列,我真正关注的不是两个指针本身,而是两个指针中间这段子序列的和,在我的理解中,如果涉及到针对子序列的操作,滑动窗口应该就是比较合适的方法了。
痛苦面具de模拟:leetcode59 螺旋矩阵2⃣️
看到这个题目转圈的过程,真没有什么好的方法,只能尝试模拟这个过程,
慢慢转呗
1,循环总次数是n*n
2,先从左上到右上,范围是(0,0) 到(n-1,0),
3,从右上到右下:范围是(n-1,1)到(n-1,n-1)
4,从右下到左下:范围是(n-2, n-1) 到(0, n-1)
5,转回到左上,范围是(0,n-2) 到(0,1)
6, 循环这么转的过程,终止条件就是移动次数为n*n
其实就是填完外面一圈后,就相当于丢掉外面一圈,而由于在循环中是四次内部的循环,分别在上,右,下,左四个边缘,因此可以用4个变量来约束我的绕圈范围 先写写看:
class Solution {
public:
vector> generateMatrix(int n) {
vectortemp(n,0);
vector>nums(n,temp);
int count = 0;
int left = 0;
int top = 0;
int bottom = n-1;
int right = n-1;//约束边缘区域
int fillnums = 1;
while(count=left; i--){//往左走
nums[bottom][i] = fillnums++;
count++;
}
bottom--;//下边往上挪
for(int i = bottom;i>=top; i--){//往上走
nums[i][left] = fillnums++;
count++;
}
left++;//左边往右挪
}
return nums;
}
}; 看上去count似乎不是那么必要,但是直觉告诉我这种代码写好了就不要改,改了容易出问题:)
今日总结:
1,做题要认真分析题目的条件和提示,就像做数学题一样一步一步分析,再去想合适的算法,不可以看到是什么类型的就直接套模版
2,滑动窗口是针对可变子序列的操作,如果题目和子序列有关,那么就应该想到滑动窗口