【动态基础】从暴力递归到动态规划
系列综述：
目的：本系列是个人整理为了秋招和实习面试的，整理期间苛求每个知识点，平衡背诵量与深入程度。
来源：材料主要源于算法大神（左程云）教你从暴力递归到动态规划进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也有少量的个人实验自证。
结语：如果有帮到你的地方，就点个赞和关注一下吧，谢谢！！！
自我检查：https://www.zhihu.com/question/585465188
文章目录
-
- 一、基础
-
- 概述
- 二、四种动规模型
-
- 边界尝试模型
-
- 概述
- 爬楼梯
- 118. 杨辉三角
- 198. 打家劫舍
- 选与不选
- 机器人走路
- 不相邻数字的最大和
- 背包问题
- 范围尝试模型
-
- 纸牌博弈
- 字符转换结果
- 动态规划：贴纸拼词
- 样本对应模型
-
- 两个字符串的最长公共子序列
- 两个字符串的最长公共子串
- 范围对应模型
-
- 最长回文子序列长度
- 象棋走路的次数
- 参考博客
点此到文末惊喜↩︎
一、基础
概述
- 递归尝试模型
- 本质是一颗遍历的树，可以通过树模型进行优化（如剪枝）
- 递归结束条件就是叶子结点的符合条件
- 动态规划的本质
- 以空间换时间：后面的计算会用到前面计算的值，从而使用
记录表减少重复的计算
// 斐波那契数列的递归 int f(int n) { if (n == 1) return 1; if (n == 2) return 2; return f(n-1) + f(n-2); } // 优化 int f(int n) { // 健壮性检查 if (n <= 1) return n; // dp数组及初始化 vector<int> dp(n+1, 0); dp[1] = 1; dp[2] = 1; // 递推 for (int i = 3; i < n; ++i) { dp[i] = dp[i-1] + dp[i-2]; } // 返回结果 return dp[n]; } - 以空间换时间：后面的计算会用到前面计算的值，从而使用
- 套路
- 通过尝试，实现暴力递归
- 确定回溯函数的参数
- 确定回溯函数出口：结束情况、失败情况、不合理情况、边界情况
- 确定正常情况：相加、求两者最值
int a=; int b=; return max(a,b)、
- 分析暴力递归的重复调用
- 以状态中的变化参数为维度，建立状态记录表dp
- 根据回溯出口条件初始化dp（初始化第一行和第一列是为了避免dp[i-1][j-1]的越界）
- 固定一个维度，进行dp表的填写
- 输出结果
- 通过尝试，实现暴力递归
- 尝试模型
- 自左向右模型：在线性数组内，从左向右对每一个元素进行尝试，确定是否选定该元素
- 范围尝试模型：明确知道L和R两个边界，左下半区无用
- 样本对应模型：两个参数就是下标，明确知道变化范围
- 业务限制模型：限制不够，业务来凑，无法明确知道变化范围
- 动态规划和递归的关系
- 递归问题包含动态规划问题，任何动态规划问题都可以由递归形式改成
二、四种动规模型
边界尝试模型
概述
- 线性数组的递归尝试
- 递归结束情况
- 边界情况
- 中间情况
爬楼梯
- 问题
- 可以从n个数字中任意选择多个，求数字之和的最大绝对值
- 思路
- 自右向左的边界尝试
- 递归出口：最左的初始化状态
- 递归算法：根是对孩子结点的运算，孩子结点是之前状态结果
- 自右向左的边界尝试
- 递归修改为动态规划
- 利用递归出口进行dp数组初始化
// 递归形式
int climbStairs(int n) {
// 递归出口
if(n == 1) return 1;
if(n == 2) return 2;
// 当前递归层的逻辑处理 加法
// 进入下一层递归 climbStairs(n - 1) 和 climbStairs(n - 2)
return climbStairs(n - 1) + climbStairs(n - 2);
}
// 改成动态规划
int climbStairs(int n) {
// 声明并初始化dp数组
vector<int> dp(n+1, 0);
dp[0] = 1;
dp[1] = 1;
// 状态转移计算
for (int i = 2; i <= n; ++i) {
dp[i] = dp[i-1] + dp[i-2];//状态转移公式
}
return dp[n];
}
118. 杨辉三角
- 问题
- 可以从n个数字中任意选择多个，求数字之和的最大绝对值
- 思路
// 递归形式
vector<vector<int>> res; //总结果
void f(int n){
// 基本情况
if(n==1) {
res={{1}};
return;
}
if(n==2) {
res={{1},{1,1}};
return;
}
// 先递归后处理
f(n-1); //递归到特殊情况
// 自左向右的处理
vector<int> prev = res.back(); // 获取上一行
vector<int> cur(prev.size()+1, 0); // 初始化大小
cur[0] = cur[cur.size()-1] = 1; // 首尾赋值
for (int i = 1; i < cur.size()-1; ++i) {
cur[i]=prev[i]+prev[i-1];
}
res.push_back(cur); //插入到结果中
}
vector<vector<int>> generate(int numRows) {
f(numRows);
return res;
}
// 动态规划（基本状态转换）
vector<vector<int>> generate(int numRows) {
// 声明并初始化DP数组
vector<vector<int>> dp(numRows);
for (int i = 0; i < numRows; ++i) {
dp[i] = vector<int>(i + 1, 1);
}
// 状态转移
for (int i = 2; i < numRows; ++i) { // 自顶向下每一行
for (int j = 1; j < i; ++j) { // 自左向右每一列
// 状态转移公式
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
return dp;
}
198. 打家劫舍
- 问题
- 求从数组中取任意个数的最大和，其中
- 思路
// 自左向右的尝试模型
int Func(const vector<int> &vec, int pos) {
if (pos == 0) return vec[0];
if (pos == 1) return max(vec[0], vec[1]);
// 从左向右的尝试模型（左边是历史状态，右边是当前状态）
int a = vec[pos] + Func(vec, pos-2);// 区分 状态集 和 单个状态
int b = Func(vec, pos-1);
return max(a, b);
}
// 动态规划
int rob(vector<int>& vec) {
// 健壮性检查
const int n = vec.size();
if (n == 0) return 0;
if (n == 1) return vec[0];
// 初始化dp数组
vector<int> dp(n);
dp[0] = vec[0];
dp[1] = max(vec[0], vec[1]);
// 状态转移
for (int i = 2; i < n; ++i) {
dp[i] = max(vec[i] + dp[i-2], dp[i-1]);
}
// 返回
return dp[n-1];
}
选与不选
- 问题
- 可以从n个数字中任意选择多个，求数字之和的最大绝对值
- 代码
// 从左向右取或不取的模型 using ll = long long; ll dfs(int right, const vector<ll> &c) { // 遍历完成，因为遍历到数组外，无论选不选都不会影响 if (right == c.size()) return 0; // 选择当前元素 ll acquire = dfs(right+1,c) + c[right]; // 放弃当前元素 ll abandon = dfs(right+1,c); // 求两者最大值 ll max_val = max(abs(acquire), abs(abandon)); return max_val; }
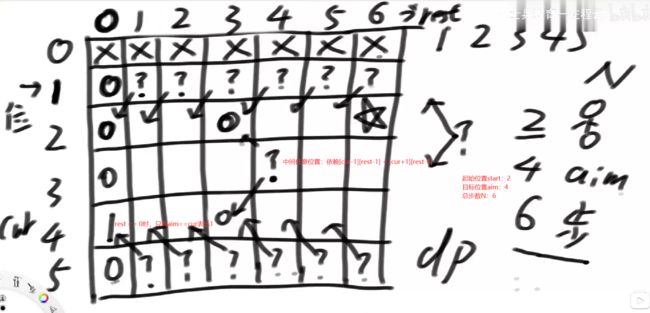
机器人走路
- 结论：
- 先将
递归尝试写出来进行处理，不要直接推导动态规划公式 - 适合场景：从[0···i]有多少种方法
- 先将
- 机器人到目标位置的路线方法数量
- start：表示机器人起始位置
- aim：表示机器人目标位置
- K：机器人可以走的步数
- N：位置总数
- 其中在0和N-1处机器人只能向中间移动，不能溢出
// 机器人当前位置为cur，还能走rest步数，最终目标是aim，总共位置1~N
// 返回机器人从cur出发走rest步数，最终到aim的方法数
// cur和rest构成转换的状态
int Try(int cur, int rest, int aim, int N) {
// 递归出口：结束条件
if (rest == 0)
return cur == aim ? 1 : 0;
// 边界情况
if (cur == 1)// 最左位置：只能从1到2
return Try(2, rest-1, aim, N);
if (cur == N)// 最右位置：只能从N到N-1
return Try(N-1, rest-1, aim, N);
// 中间情况
return Try(cur-1, rest-1, aim, N) + Try(cur+1, rest-1, aim, N);
}
- 递归尝试的傻缓存优化
- 增加dp缓存表：值初始化为标记量，用于标记是否使用过
- 判断是否能命中缓存表：命中则直接返回，未命中则执行
- 将递归return使用值记录
// 优化：自顶向下的动态规划/记忆化搜索
// 状态空间：cur范围1~N，rest范围0~K，这就是dp的行列属性
// dp就是缓存表，dp[i][j] == -1表示计算过
vector<vector<int>> dp(N+1, vector(K+1, -1));
int Try2(int cur, int K, int aim, int N, vector<vector<int>> &dp) {
// 计算过的通过缓存表直接返回
if (dp[cur][rest] != -1)
return dp[cur][rest];
// 没计算过，则无法返回
int ans = 0;
if (rest == 0) {
ans = (cur == aim ? 1 : 0);
}else if(cur == 1) {
ans = Try2(2, rest-1, aim, N, dp);
}else if(cur == N) {
ans = Try2(N-1, rest-1, aim, N, dp);
}else {
ans = Try(cur-1, rest-1, aim, N, dp) +
Try(cur+1, rest-1, aim, N, dp);
}
dp[cur][rest] = ans;
return ans;
}
int res = dp[N][K];// 返回结果
- 真正的动态规划
- 明确dp数组的含义
- 根据递归尝试对dp数组进行改进
int Try3(int cur, int K, int aim, int N) {
// 健壮性检查
if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1){
return -1;
}
// dp数组声明
vector<vector<int>> dp(N+1, vector(K+1, 0));
// dp数组初始化
dp[aim][0] = 1;// 0步则只有aim位置为1，其他位置初始化为0
for (int rest = 1; rest <= K; ++rest) {
// 第一个行只依赖左下角
dp[1][rest] = dp[2][rest-1];
// 中间行依赖左上和左下
for (int cur = 2; cur < N; ++cur) {// 不在循环中进行判断可以减少判断
dp[cur][rest] = dp[cur-1][rest-1] + dp[cur+1][rest-1];
}
// 最后一行依赖左上
dp[N][rest] = dp[N-1][rest-1];
}
return dp[start][K];// 表示从start位置走到K的次数
}
不相邻数字的最大和
- 问题
- 在数组中取出一个或多个不相邻数，使其和最大，即找到max(不相邻元素组成的子数组)。
- 递归尝试
- 从右向左的尝试模型
int MaxSum(vector<int> vec, int p) { // 递归结束情况 if (p == 0) // 只有一个元素时 return vec[0]; else if (p == 1) // 只有两个元素时 return max(vec[0], vec[1]); else { // 其他情况 int a = MaxSum(vec, p-2) + vec[p]; int b = MaxSum(vec, p-1); return max(a, b); // 选两边与选中间取最大值 } } - 动态规划
int
public static int dp_opt(int[] arr) {
int[] opt = new int[arr.length];
opt[0] = arr[0];
opt[1] = Math.max(arr[0], arr[1]);
for(int i=2; i<arr.length; i++) {
int a = opt[i-2] + arr[i];
int b = opt[i-1];
opt[i] = Math.max(a, b);
}
return opt[arr.length-1];
}
背包问题
- 问题
- 给定两个长度都为 N 的数组 weights 和 values，weights[i] 和 values[i] 分别代表 i 号物品的重量和价值。
- 给定一个正数 bag，表示一个载重 bag 的袋子，你装的物品不能超过这个重量。
- 请问你能装下最多的价值是多少
- 暴力版本
public class Knapsack { //所有的货，重量和价值，都在w和v数组中 //为了方便，其中没有负数 //bag背包容量，不能超过这个载重 //返回：不超重的情况下，能够得到的最大价值 public static int maxValue(int[] w, int[] v, int bag) { if (w == null || v == null || w.length != v.length || w.length == 0) return 0; //尝试函数 return process(w, v, 0, bag); } //当前考虑到了index号货物，index...的所有货物可以自由选择 //做的选择不能超过背包容量 //返回最大价值 public static int process(int[] w, int[] v, int index, int rest) { if (rest < 0) { return -1; } if (index == w.length) { return 0; } //有货，index位置的货 //bag有空间，0 //不要当前的货 int p1 = process(w, v, index + 1, rest); //要当前的货 int p2 = 0; // key：避免选择0号货物失败但仍然计算进去的问题 int next = process(w, v, index + 1, rest - w[index]); if (next != -1) { //处理w = 7， v = 15，bag = 6类似的情况，后续有效才加 p2 = v[index] + next; } return Math.max(p1, p2); } public static void main(String[] args) { int[] weights = {3, 2, 4, 7}; int[] values = {5, 6, 3, 19}; int bag = 11; System.out.println(maxValue(weights, values, bag)); } } - 转换成动态规划
public class Knapsack { public static int dpWay(int[] w, int[] v, int bag) { if (w == null || v == null || w.length != v.length || w.length == 0) return 0; int n = w.length; //index：0 ~ n //rest：负 ~ bag int[][] dp = new int[n + 1][bag + 1]; //动态规划表 //dp[n][...] = 0 //从递归函数可以看到，index行是依赖于index+1的，所以倒着填，同行之间是不互相依赖的 for (int index = n - 1; index >= 0; index--) { //从下往上填 for (int rest = 0; rest <= bag; rest++) { int p1 = dp[index + 1][rest]; int p2 = 0; int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]]; if (next != -1) { p2 = v[index] + next; } dp[index][rest] = Math.max(p1, p2); } } return dp[0][bag]; //返回什么值，由暴力递归的调用函数决定，调用时传的什么值就是最后动态规划要返回的值 } public static void main(String[] args) { int[] weights = {3, 2, 4, 7}; int[] values = {5, 6, 3, 19}; int bag = 11; System.out.println(dpWay(weights, values, bag)); } }
范围尝试模型
- 适应情况
- 每次只考虑左右边界情况
- 从[i…j]有多少种情况
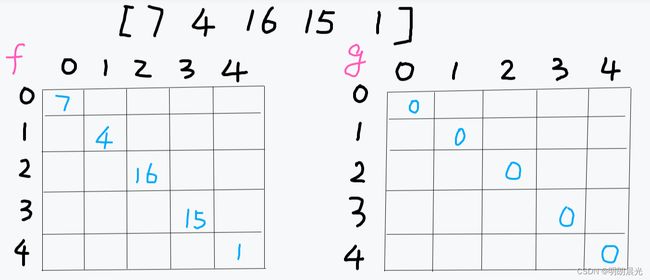
纸牌博弈
- 问题
- 给定一个整型数组 arr，代表数值不同的纸牌排成一条线。
- 玩家A 和 玩家B 依次拿走每张纸牌。
- 规定玩家 A 先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。
- 请返回最后获胜者的分数。
// 递归尝试 public class CardsInLine { //根据规则，返回获胜者的分数 public static int win1(int[] arr) { if (arr == null || arr.length == 0) return 0; int first = f(arr, 0, arr.length - 1); int second = g(arr, 0, arr.length - 1); return Math.max(first, second); } //arr[l...r] 先手获得的最好分数返回 public static int f(int[] arr, int l, int r) { if (l == r) return arr[l];// 只有一张牌，先手必胜 int p1 = arr[l] + g(arr, l + 1, r);// 先手拿走左侧牌，剩下牌是后手姿态 int p2 = arr[r] + g(arr, l, r - 1);// 先手拿走右侧牌，剩下牌是先手姿态 return Math.max(p1, p2);// 先手可以获得最大分值 } //arr[l...r]，后手获得的最好分数返回 public static int g(int[] arr, int l, int r) { if (l == r) return 0; int p1 = f(arr, l + 1, r); //对手拿走了l位置的数 int p2 = f(arr, l, r - 1); //对手拿走了r位置的数 return Math.min(p1, p2); } } - 根据递归函数分析位置依赖
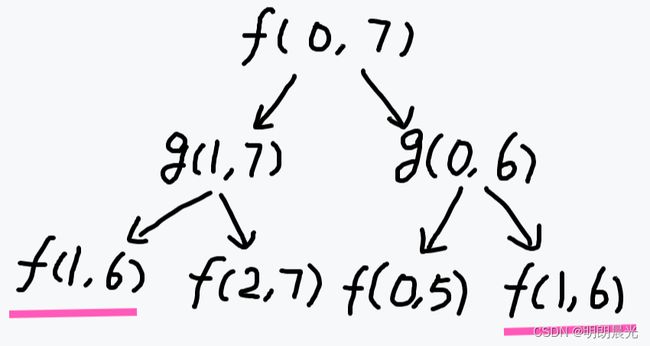
- 将计算结果进行状态记录——傻缓存
- 分别给f和g建立一张表
public class CardsInLine { public static int win2(int[] arr) { if (arr == null || arr.length == 0) return 0; int n = arr.length; //根据可变参数l和r的范围准备两张表 int[][] fmap = new int[N][N]; int[][] gmap = new int[N][N]; for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { fmap[i][j] = -1; gmap[i][j] = -1; } } int first = f2(arr, 0, arr.length - 1, fmap, gmap); int second = g2(arr, 0, arr.lenght - 1, fmap, gmap); return Math.max(first, second); } //arr[l...r]，先手获得的最好分数返回 public static int f2(int[] arr, int l, int r, int[][] fmap, int[][] gmap) { if (fmap[l][r] != -1) return fmap[l][r]; int ans = 0; if (l == r) { ans = arr[l]; } else { int p1 = arr[l] + g2(arr, l + 1, r, fmap, gmap); int p2 = arr[r] + g2(arr, l, r - 1, fmap, gmap); ans = Math.max(p1, p2); } fmap[l][r] = ans; return ans; } //arr[l...r]，后手获得的最好分数返回 public static int g2(int[] arr, int l, int r, int[][] fmap, int[][] gmap) { if (gmap[l][r] != -1) return gmap[l][r]; int ans = 0; if (l != r) { int p1 = f2(arr, l + 1, r, fmap, gmap); int p2 = f2(arr, l, r - 1, fmap, gmap); ans = Math.min(p1, p2); } gmap[l][r] = ans; return ans; } public static void main(String[] args) { int[] arr = {5, 7, 4, 5, 8, 1, 6, 0, 3, 4, 6, 1, 7}; System.out.println(win2(arr)); } } - 动态规划
- 当
l == r时，即表中的对角线应该填充的数
l>r是无效部分，因为l>r时，表示无可用牌了
- 分析元素对于表的依赖关系：f 表依赖于 g 表，那么在 f 表的有效普遍位置中在 g 表找到一个对称的位置，然后找到依赖关系（f表中元素依赖于g表中对应位置左边和下边的元素）
- g 表依赖于 f 表的原理关系
- 根据 f 的对角线值推出g 表的值；同理，得到了 g 表的值之后可以倒推 f 表的值
- 当
public class CardsInLine {
public static int win3(int[] arr) {
if (arr == null || arr.length == 0) return 0;
int n = arr.length;
//根据可变参数l和r的范围准备两张表
int[][] fmap = new int[n][n];
int[][] gmap = new int[n][n];
for (int i = 0; i < n; i++) {
fmap[i][i] = arr[i]; //填充对角线的值
}
for (int startCol = 1; startCol < n; i++) {
int l = 0;
int r = startCol;
while (r < n) {
//上面推导出来的位置依赖关系
fmap[l][r] = Math.max(arr[l] + gmap[l + 1][r], arr[r] + gmap[l][r - 1]);
gmap[l][r] = Math.min(fmap[l + 1][r], fmap[l][r - 1]);
l++;
r++;
}
}
return Math.max(fmap[0][n - 1], gmap[0][n - 1]);
}
}
字符转换结果
- 问题
- 规定 1 和 A 对应、2 和 B 对应、3 和 C 对应… 26 和 Z 对应。
- 那么一个数字字符串比如 “111” 就可以转化为：“AAA”、“KA” 和 “AK”。
- 给定一个只有数字字符组成的字符串 str，返回有多少种转化结果。
- 尝试暴力回溯
- 尝试模型就是1+N的情况的分析，特别是针对1进行分析
public class CovertToLetterString { //str 只含有数字字符0~9 //返回多少种转化方案 public static int number(String str) { if (str == null || str.length == 0) return 0; return process(str.toCharArray(), 0); } //str[0..i-1] 转化无需过问 //str[i...] 去转化，有多少种转化方法 public static int process(char[] str, int i) { // 结束情况 if (i == str.length) return 1; // 终止位置是收集一种方法 // 不符合题意的情况 // 0不对应任意一个字符，如果单独出现说明之前的都错了 if (str[i] == '0') return 0; // str[i] != '0' // 可能性1：i单转 int ways = process(str, i + 1); // 可能性2：i 和 i+1位置一起转,两个位置结合的值小于27才有效 if (i + 1 < str.length && (str[i] - '0') * 10 + str[i + 1] - '0' < 27) ways += process(str, i + 2); return ways; } public static void main(String[] args) { System.out.println(number("111111")); } } - 修改为动态规划
public class ConvertToLetterString { public static int dpWay(String s) { if (s == null || s.length == 0) return 0; char[] str = s.toCharArray(); int n = str.lenght; int[] dp = new int[n + 1]; dp[n] = 1; //根据位置依赖，依赖于其后面的位置，所以从右往左填 for (int i = n - 1; i >= 0; i--) { //在递归函数里做的事情就直接到dp表中取数据即可 if (str[i] != '0') { int ways = dp[i + 1]; if (i + 1 < str.length && (str[i] - '0') * 10 + str[i + 1] - '0' < 27) { ways += dp[i + 2]; } dp[i] = ways; } } return dp[0]; } public static void main(String[] args) { System.out.println(dpWay("111111")); } }
动态规划：贴纸拼词
- 问题（leetcode链接）
- 贴纸数组：每个贴纸都是一个小写的英文单词，并且每个贴纸可以用无数次
- 目标单词：选取尽可能少的贴纸，通过贴纸裁剪拼出目标单词
- 本质：最少贴纸中的单词可以覆盖目标单词
- 思路
- 无论几张贴纸，肯定有其中一张作为第一个
- 排序可以提高命中率
- 代码
public class StickersToSpellWord { public static int minStickers(String[] stickers, String target) { int ans = process(stickers, target); return ans == Integer.MAX_VALUE ? -1 : ans; //-1 表示无论如何都拼不出target } //所有贴纸stickers，每种贴纸都有无穷张 //拼成targett //返回需要的最少张数 public static int process(String[] stickers, String target) { if (target.length() == 0) return 0; int min = Integer.MAX_VALUE; //剩余还需要的最小贴纸张数 for (String first : stickers) { //每张贴纸都作为第一张的情况 String rest = minus(target, first);// target中减去first中含有的对应字符 if (rest.length() != target.length()) { min = Math.min(min, process(stickers, rest)); //除了第一张还需要的贴纸，第一张还没被算进去 } } return min + (min == Integer.MAX_VALUE ? 0 : 1); //+1是加上first这张贴纸 } public static String minus(String s1, String s2) { char[] str1 = s1.toCharArray(); char[] str2 = s2.toCharArray(); int[] count = new int[26]; for (char cha : str1) count[cha - 'a']++; for (char cha : str2) count[cha - 'a']--; StringBuilder builder = new StringBuilder(); for (int i = 0; i < 26; i++) { if (count[i] > 0) { for (int j = 0; j < count[i]; j++) { builder.append((char) (i + 'a')); } } } return builder.toString(); } } - 优化
class Solution { public: int process(vector<vector<int>> &stickers, string target, unordered_map<string, int> &dp) { if (dp.count(target)) return dp[target]; //统计target词频 vector<int> tcount(26, 0); for (char ch : target) { tcount[ch - 'a']++; } int ans = INT_MAX; int n = stickers.size(); for (int i = 0; i < n; i++) { vector<int> sticker = stickers[i]; if (sticker[target[0] - 'a'] > 0) { string rest = ""; for (int j = 0; j < 26; j++) { if (tcount[j] > 0) { int nums = tcount[j] - sticker[j]; for (int k = 0; k < nums; k++) { rest.push_back(j + 'a'); } } } ans = min(ans, process(stickers, rest, dp)); } } int res = ans + (ans == INT_MAX ? 0 : 1); dp[target] = res; return res; } int minStickers(vector<string>& stickers, string target) { //统计stickers中的词频 int n = stickers.size(); vector<vector<int>> counts(n, vector<int>(26, 0)); for (int i = 0; i < n; i++) { for (char ch : stickers[i]) { counts[i][ch - 'a']++; } } //缓存表 unordered_map<string, int> dp; dp[""] = 0; int ans = process(counts, target, dp); return ans == INT_MAX ? -1 : ans; } };
样本对应模型
两个字符串的最长公共子序列
- 概述
- 样本对应模型一般只以最后一个位置作为可能性的讨论
- 给定两个样本（串或序列） ，输出它们对应的解
- 感觉是从右向左的尝试模型
- 问题（leetcode链接）
- 给定两个字符串 str1 和 str2，返回这两个字符串的最长公共子序列长度(不连续)。
- 输入：
12bj3hglihlkgb123afa输出：123 - https://blog.csdn.net/qq_39622795/article/details/115427653
// # 递归方法
int longestConmmonSubsequence(string s1, string s2) {
// 健壮性检查
if (s1.size() == 0 || s2.size() == 0) return 0;
// 算法部分：封装函数，输入两个最长公共子序列，输出其公共子序列长度
return process(s1, s2, s1.size()-1, s2.size()-1);
}
// 返回s1[0~i]与s2[0~j]的最长公共子序列长度
int process(string s1, string s2, int i, int j) {
if (i == 0 && j == 0) {// 避免j-1的越界
return s1[i] == s2[j] ? 1 : 0;
} else if (i == 0) {// 只有一个字符
if(s1[i] == s2[j]) {// 在s2中找到对应的
return 1;
} else {
return process(s1, s2, i, j-1);// 没找到，找剩下的
}
} else if (j == 0) {
if(s1[i] == s2[j]) {// 在s2中 找到对应的
return 1;
} else {
return process(s1, s2, i-1, j);// 没找到，找剩下的
}
} else { // 都不为零
// 因为求的是子序列，所以可以对其中一个完全不考虑
int p1 = process(s1, s2, i-1, j); // 完全不考虑i，但可能考虑j
int p2 = process(s1, s2, i, j-1); // 可能考虑i，但完全不考虑j
// 两者结尾的情况都考虑：最后一位确定为1+判断前面的
int p3 = s1[i] == s2[j] ? (1 + process(s1, s2, i-1, j-1)) : 0;
return max(p1, max(p1, p2));
}
}
// # 动规方法
int longestConmmonSubsequence(string s1, string s2) {
// 健壮性检查
if (s1.size() == 0 || s2.size() == 0) return 0;
int N = s1.size();
int M = s2.size();
vector<vector<int>> dp(N, vector(M,0));
dp[0][0] = s1[0] == s2[0] ? 1 : 0;
// 第0行
for (int j = 1; j < M; ++j) {
dp[0][j] = s1[0] == s2[j] ? 1 : dp[0][j-1];
}
// 第0列
for (int i = 1; i < N; ++i) {
dp[i][0] = s1[i] == s2[0] ? 1 : dp[i-1][0];
}
//
for (int i = 1; i < N; ++i) {
for (int j = 1; j < M; ++j) {
int p1 = dp[i-1][j]; // 完全不考虑i，但可能考虑j
int p2 = dp[i][j-1]; // 可能考虑i，但完全不考虑j
// 两者结尾的情况都考虑：最后一位确定为1+判断前面的
int p3 = s1[i] == s2[j] ? (1 + dp[i-1][j-1]) : 0;
dp[i][j] = max(p1, max(p2, p3));
}
}
return dp[N-1][M-1];
}
两个字符串的最长公共子串
- 思路
- 把两个字符串分别以行和列组成一个二维矩阵。
- 比较二维矩阵中每个点对应行列字符中否相等，相等的话值设 置为1，否则设置为0。
- 通过查找出值为1的最长对角线就能找到最长公共子串。
// record[i][j]表示x1~xi与y1~yj的最长公共子串的长度 string getLCS(string str1, string str2) { vector<vector<int> > record(str1.length(), vector<int>(str2.length())); int maxLen = 0, maxEnd = 0; for(int i=0; i<static_cast<int>(str1.length()); ++i) for (int j = 0; j < static_cast<int>(str2.length()); ++j) { if (str1[i] == str2[j]) { if (i == 0 || j == 0) {// 避免越界 record[i][j] = 1; } else { record[i][j] = record[i - 1][j - 1] + 1; } } else { record[i][j] = 0; } if (record[i][j] > maxLen) { maxLen = record[i][j]; maxEnd = i; //若记录i,则最后获取LCS时是取str1的子串 } } return str1.substr(maxEnd - maxLen + 1, maxLen); }
范围对应模型
最长回文子序列长度
- 问题（leetcode链接）
- 回文是左右对称的序列，序列在原串中可以不用连续
- 输入：str = “a12b3c43def2ghi1kpm”
- 输出：“1234321”或者"123c321”
- 思路
- 样本对应模型：主串与逆序串的最长公共子序列，就是其最长回文子序列
- 范围对应模型：考虑开头和结尾的情况
- 递归转回溯
- 根据回溯进行dp数组的初始化
- 分析依赖关系，两层for循环进行依赖处理
// 主调函数
int longestPalindromeSubseq(string s) {
if (s.size() == 0) return 0;
return f(s, 0, s.size()-1);
}
// 递归算法
int f(string s, int left, int right) {
if (left == right){ // 只有一个字符
return 1;
}
if (left == right - 1) {// 有两个字符
return s[left] == s[right] ? 2 : 1;
}
int p1 = f(s, left + 1, right - 1); // 不以left开头，不以right结尾
int p2 = f(s, left , right - 1); // 以left开头，但不以right结尾
int p3 = f(s, left + 1, right); // 以right结尾，但不以left开头
int p4 = s[left] == s[right] ? (2 + // 以left开头，又以right结尾
f(s, left + 1, right - 1)) : 0;
return max(max(p1, p2), max(p3, p4));
}
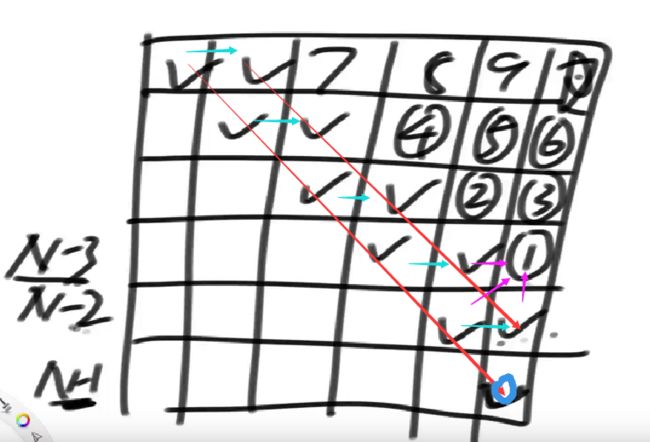
// 动态规划：s[i...j]中i
int f(string s) {
if (s.size() == 0) {
return 0;
}
int N = s.size();
vector<vector<int>> dp(N, vector<int>(N));
// 填对角线
for (int i = 0; i < N; ++i) {
dp[i][i] = 1;
}
// 填左上的第二条对角线：相邻的相等为2，不相等为1
for (int i = 0; i < N-1; ++i) {// 第二对角线最后少一个
dp[i][i+1] = s[i] == s[i+1] ? 2 : 1;
}
/*
// 一次填充两个对角线
dp[N-1][N-1] = 1;// 将左下角填入
// 每一行填相邻的两个对角线元素
for (int i = 0; i < N-1; ++i) {
dp[i][i] = 1;
dp[i][i+1] = (str[i] == str[i+1]) ? 2 : 1;
}
*/
for (int L = N-3; L >= 0; --L) {
for(int R = L+2; R < N; ++R) {
// dp表分析，每个位置都依赖于其左、下、左下，所以左和下都比左下大，即p1可以优化掉
//int p1 = dp[L+1][R-1]; // 不以left开头，不以right结尾
int p2 = dp[L][R-1]; // 以left开头，但不以right结尾
int p3 = dp[L+1][R]; // 以right结尾，但不以left开头
int p4 = s[L] == s[R] ? (2 + // 以left开头，又以right结尾
dp[L+1][R-1]) : 0;
dp[L][R] = max(max(p1, p2), max(p3, p4));
/* 优化：推导严格的位置依赖
dp[L][R] = max(dp[L][R-1], dp[L+1][R]);
if (s[L] == s[R]) {
dp[L][R] = max(dp[L][R], 2+dp[L+1][R-1]);
}
*/
}
}
return dp[0][N-1];// 最后一个填入的格子
}
象棋走路的次数
- 问题（leetcode链接）
// 在一个10*9的棋盘上， 从当前位置（x, y）跳rest步，正好跳到(a, b)的方法数
int jump(int x, int y, int rest, int a, int b) {
// 越界的情况
if(x < 0 || x > 9 || y < 0 || y > 8) {
return 0;
}
// 成功跳到目标位置
if (rest == 0) {
return (x == a && y == b) ? 1 : 0;
}
int ways = jump(x+2, y+1, rest-1, a, b);
ways += jump(x+1, y+2, rest-1, a, b);
ways += jump(x-1, y+2, rest-1, a, b);
ways += jump(x-2, y+1, rest-1, a, b);
ways += jump(x-2, y-1, rest-1, a, b);
ways += jump(x-1, y-2, rest-1, a, b);
ways += jump(x+1, y-2, rest-1, a, b);
ways += jump(x+2, y-1, rest-1, a, b);
return ways;
}
// 动态规划方法
int jump(int x, int y, int rest, int a, int b) {
// 越界的情况
auto pick = [](vector<vector<vector<int>>> &dp, int x, int y, int rest)->int{
if(x < 0 || x > 9 || y < 0 || y > 8) {
return 0;
}
return dp[x][y][rest];
}
// dp数组是变化的维度
vector<vector<vector<int>>> dp(a, vector<vector<int>>(b, vecto<int>(rest, 0)));
dp[a][b][0] = 1;
for(int i = 1; rest <= k; rest++) {
for (int x = 0; x < 10; ++x) {
for (int y = 0; y < 9; ++y) {
int ways = pick(dp, x+2, y+1, rest-1);
ways += pick(dp, x+1, y+2, rest-1);
ways += pick(dp, x-1, y+2, rest-1);
ways += pick(dp, x-2, y+1, rest-1);
ways += pick(dp, x-2, y-1, rest-1);
ways += pick(dp, x-1, y-2, rest-1);
ways += pick(dp, x+1, y-2, rest-1);
ways += pick(dp, x+2, y-1, rest-1);
dp[x][y][rest] = ways; // 所有return都是给dp的赋值
}
}
}
return dp[0][0][k];
}
点此跳转到首行↩︎
参考博客
- 算法大神（左程云）教你从暴力递归到动态规划
- 动态规划：拿纸牌游戏
- 代码随想录
- 《深入理解计算机系统》
- 侯捷C++全系列视频
- 爬楼梯-递归
- 待定引用
- 待定引用