EM算法解析+代码
大纲
- 数学基础:凸凹函数,Jensen不等式,MLE
- EM算法公式,收敛性
- HMM高斯混合模型
一、数学基础
1. 凸函数
通常在实际中,最小化的函数有几个极值,所以最优化算法得出的极值不确实是否为全局的极值,对于一些特殊的函数,凸函数与凹函数,任何局部极值也是全局极致,因此如果目标函数是凸的或凹的,那么优化算法就能保证是全局的。
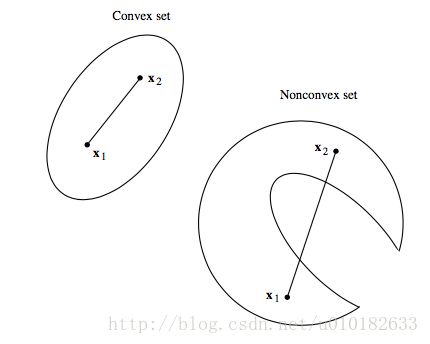
定义1:集合 R c ⊂ E n R_c\subset E^n Rc⊂En是凸集,如果对每对点 x 1 , x 2 ⊂ R c \textbf{x}_1,\textbf{x}_2\subset R_c x1,x2⊂Rc,每个实数 α , 0 < α < 1 \alpha,0<\alpha<1 α,0<α<1,点 x ∈ R c \textbf{x}\in R_c x∈Rc
x = α x 1 + ( 1 − α ) x 2 \textbf{x}=\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2 x=αx1+(1−α)x2
 |
 |
|---|
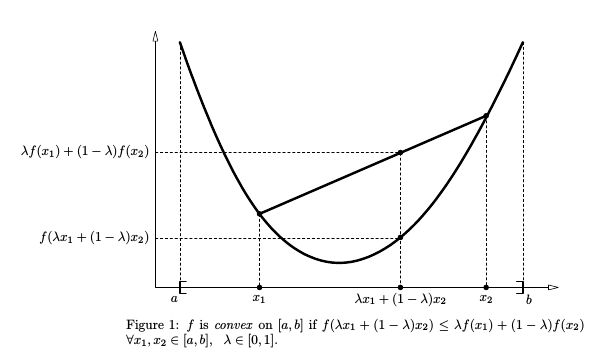
定义2:我们称定义在凸集 R c R_c Rc上的函数 f ( x ) f(x) f(x)为凸的,如果对每对 x 1 , x 2 ∈ R c \textbf{x}_1,\textbf{x}_2 \in R_c x1,x2∈Rc与每个实数 α , 0 < α < 1 \alpha ,0<\alpha<1 α,0<α<1,则满足不等式
f [ α x 1 + ( 1 − α ) x 2 ] ≤ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2]\leq\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2) f[αx1+(1−α)x2]≤αf(x1)+(1−α)f(x2)如果 x 1 ≠ x 2 \textbf{x}_1\neq\textbf{x}_2 x1=x2,则 f ( x ) f(x) f(x)是严格凸的。
f [ α x 1 + ( 1 − α ) x 2 ] < α f ( x 1 ) + ( 1 − α ) f ( x 2 ) f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2]<\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2) f[αx1+(1−α)x2]<αf(x1)+(1−α)f(x2)
2. Jensen不等式
定义1:若 f ( x ) f(x) f(x)为区间 X X X上的凸函数,则 ∀ n ∈ N , n ≥ 1 \forall n \in \mathbb N, n \ge 1 ∀n∈N,n≥1, 若 ∀ i ∈ N , 1 ≤ i ≤ n , x i ∈ X , λ i ∈ R \forall i \in \mathbb N, 1 \le i \le n, x_i \in X, \lambda_i \in \mathbb R ∀i∈N,1≤i≤n,xi∈X,λi∈R, 且 ∑ i = 1 n λ i = 1 \sum^n_{i=1}\lambda_i=1 ∑i=1nλi=1, 则:
f ( ∑ i = 1 n λ i x i ) ≤ ∑ i = 1 n λ i f ( x i ) f(\sum_{i=1}^{n} \lambda_i x_i) \le \sum_{i=1}^{n} \lambda_i f(x_i) f(i=1∑nλixi)≤i=1∑nλif(xi)
推论1:若 f ( x ) f(x) f(x)为区间 R R R上的凸函数, g ( x ) : R → R g(x): R \rightarrow R g(x):R→R为一任意函数, X X X为一取值范围有限的离散变量, E [ f ( g ( X ) ) ] E [f \left ( g(X) \right ) ] E[f(g(X))]与 E [ g ( X ) ] E[g(X)] E[g(X)]都存在,则:
E [ f ( g ( X ) ) ] ≥ f ( E [ g ( X ) ] ) E [f \left ( g(X) \right ) ] \ge f \left (E[g(X)] \right ) E[f(g(X))]≥f(E[g(X)])
3. MLE
极大似然估计方法(Maximum Likelihood Estimate,MLE)也称为最大概似估计或最大似然估计。
一般说来,事件A发生的概率与某一未知参数 θ \theta θ有关, θ \theta θ的取值不同,则事件A发生的概率 P ( A ∣ θ ) P(A|\theta) P(A∣θ)也不同,当我们在一次试验中事件A发生了,则认为此时的 θ \theta θ 值应是 t t t 的一切可能取值中使 P ( A ∣ θ ) P(A|\theta) P(A∣θ)达到最大的那一个,极大似然估计法就是要选取这样的 t t t值作为参数 t t t的估计值,使所选取的样本在被选的总体中出现的可能性为最大。
二、EM算法
1. EM算法简介
概率模型有时既含有观测变量(observable variable),又含有隐变量或潜在变量(latent variable),如果仅有观测变量,那么给定数据就能用极大似然估计或贝叶斯估计来估计model参数;但是当模型含有隐变量时,需要一种含有隐变量的概率模型参数估计的极大似然方法估计——EM算法, 称为期望极大值算法(expectation maximizition algorithm,EM),是一种启发式的迭代算法。
EM算法的思路是使用启发式的迭代方法,既然我们无法直接求出模型分布参数,那么我们可以先猜想隐含数据(EM算法的E步),接着基于观察数据和猜测的隐含数据一起来极大化对数似然,求解我们的模型参数(EM算法的M步)。
可以通过K-Means算法来简单理解EM算法的过程。
-E步:在初始化K个中心点后,我们对所有的样本归到K个类别。
-M步:在所有的样本归类后,重新求K个类别的中心点,相当于更新了均值。
2. EM算法公式
对于 m m m 个样本观察数据 x = ( x ( 1 ) , x ( 2 ) , . . . x ( m ) ) x=(x^{(1)},x^{(2)},...x^{(m)}) x=(x(1),x(2),...x(m))中,找出样本的模型参数 θ \theta θ,极大化模型分布的对数似然函数如下,
L ( θ ) = ∑ i = 1 m l o g P ( x ( i ) ∣ θ ) L(\theta) = \sum\limits_{i=1}^m logP(x^{(i)}|\theta) L(θ)=i=1∑mlogP(x(i)∣θ)
假设数据中有隐含变量 z = ( z ( 1 ) , z ( 2 ) , . . . z ( m ) ) z=(z^{(1)},z^{(2)},...z^{(m)}) z=(z(1),z(2),...z(m)), 加入隐含变量公式变为如下(E步就是估计 Q Q Q函数),
Q i ( z ( i ) ) = P ( z ( i ) ∣ x ( i ) , θ ) L ( θ ) = ∑ i = 1 m l o g ∑ z ( i ) P ( x ( i ) , z ( i ) ∣ θ ) = ∑ i = 1 m l o g ∑ z ( i ) Q i ( z ( i ) ) P ( x ( i ) , z ( i ) ∣ θ ) Q i ( z ( i ) ) s . t . ∑ z Q i ( z ( i ) ) = 1 ( 1 ) Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)},\theta) \\ L(\theta) = \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}P(x^{(i)},z^{(i)}|\theta) = \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}Q_i(z^{(i)})\frac{P(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})}\;\;\;s.t.\sum\limits_{z}Q_i(z^{(i)}) =1\;\;\;\;\;(1) Qi(z(i))=P(z(i)∣x(i),θ)L(θ)=i=1∑mlogz(i)∑P(x(i),z(i)∣θ)=i=1∑mlogz(i)∑Qi(z(i))Qi(z(i))P(x(i),z(i)∣θ)s.t.z∑Qi(z(i))=1(1)
根据Jensen不等式,(1)式变为(2), 注意到下式中 Q i ( z ( i ) ) Q_i(z(i)) Qi(z(i)) 是一个分布,因此 ∑ Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ∣ θ ) \sum Q_i(z(i))logP(x(i),z(i)|θ) ∑Qi(z(i))logP(x(i),z(i)∣θ) 可以理解为 l o g P ( x ( i ) , z ( i ) ∣ θ ) logP(x(i),z(i)|θ) logP(x(i),z(i)∣θ) 基于条件概率分布 Q i ( z ( i ) ) Q_i(z(i)) Qi(z(i)) 的期望。
E [ f ( g ( X ) ) ] ≤ f ( E [ g ( X ) ] ) ( 凹函数 ) L ( θ ) = ∑ i = 1 m l o g ∑ z ( i ) Q i ( z ( i ) ) P ( x ( i ) , z ( i ) ∣ θ ) Q i ( z ( i ) ) ≥ ∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ∣ θ ) Q i ( z ( i ) ) s . t . ∑ z Q i ( z ( i ) ) = 1 ( 2 ) E [f \left ( g(X) \right ) ] \le f \left (E[g(X)] \right ) \ (凹函数) \\ L(\theta) = \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}Q_i(z^{(i)})\frac{P(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})}\ge\sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})}\;\;\;s.t.\sum\limits_{z}Q_i(z^{(i)}) =1\;\;\;\;\;(2) E[f(g(X))]≤f(E[g(X)]) (凹函数)L(θ)=i=1∑mlogz(i)∑Qi(z(i))Qi(z(i))P(x(i),z(i)∣θ)≥i=1∑mz(i)∑Qi(z(i))logQi(z(i))P(x(i),z(i)∣θ)s.t.z∑Qi(z(i))=1(2)
第(2)式是我们的包含隐藏数据的对数似然的一个下界。如果我们能极大化这个下界,则也在尝试极大化我们的对数似然。即我们需要最大化下式:
∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ∣ θ ) Q i ( z ( i ) ) \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)},z^{(i)}|\theta)}{Q_i(z^{(i)})} i=1∑mz(i)∑Qi(z(i))logQi(z(i))P(x(i),z(i)∣θ)
去掉上式中为常数的部分,则我们需要极大化的对数似然下界为:
a r g max θ ∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ; θ ) arg \max \limits_{\theta} \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)}, z^{(i)};\theta)} argθmaxi=1∑mz(i)∑Qi(z(i))logP(x(i),z(i);θ)
3. EM算法流程
输入:观察数据 x = ( x ( 1 ) , x ( 2 ) , . . . x ( m ) ) x=(x^{(1)},x^{(2)},...x^{(m)}) x=(x(1),x(2),...x(m)),联合分布 p ( x , z ∣ θ ) p(x,z|\theta) p(x,z∣θ), 条件分布 p ( z ∣ x , θ ) p(z|x,\theta) p(z∣x,θ), EM算法退出的阈值 γ \gamma γ。
- 随机初始化模型参数 θ \theta θ 的初值 θ 0 \theta^0 θ0。
- E步:求Q函数(联合分布的条件概率期望),对于每一个i,计算根据上一次迭代的模型参数来计算出隐性变量的后验概率(其实就是隐性变量的期望),来作为隐藏变量的现估计值 Q i ( z ( i ) ) = P ( z ( i ) ∣ x ( i ) , θ j ) L ( θ , θ j ) = ∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ∣ θ ) Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)},\theta^{j}) \\ L(\theta, \theta^{j}) = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)},z^{(i)}|\theta)} Qi(z(i))=P(z(i)∣x(i),θj)L(θ,θj)=i=1∑mz(i)∑Qi(z(i))logP(x(i),z(i)∣θ)
- M步:极大化 L ( θ , θ j ) L(\theta,\theta^j) L(θ,θj), 得到 θ j + 1 : θ j + 1 = a r g max θ L ( θ , θ j ) θ^{j+1}: \theta^{j+1} = arg \max\limits_{\theta}L(\theta, \theta^{j}) θj+1:θj+1=argθmaxL(θ,θj)
- 重复2,3两步,直到极大似然估计 L ( θ , θ j ) L(\theta,\theta^j) L(θ,θj) 的变化小于 γ \gamma γ
如果我们从算法思想的角度来思考EM算法,我们可以发现我们的算法里已知的是观察数据,未知的是隐含数据和模型参数,在E步,我们所做的事情是固定模型参数的值,优化隐含数据的分布,而在M步,我们所做的事情是固定隐含数据分布,优化模型参数的值。
4. EM算法的收敛性思考
EM算法的流程并不复杂,但是还有两个问题需要我们思考:
1) EM算法能保证收敛吗?
2) EM算法如果收敛,那么能保证收敛到全局最大值吗?
首先我们来看第一个问题, EM算法的收敛性。要证明EM算法收敛,则我们需要证明我们的对数似然函数的值在迭代的过程中一直在增大。即:
∑ i = 1 m l o g P ( x ( i ) ; θ j + 1 ) ≥ ∑ i = 1 m l o g P ( x ( i ) ; θ j ) \sum\limits_{i=1}^m logP(x^{(i)};\theta^{j+1}) \geq \sum\limits_{i=1}^m logP(x^{(i)};\theta^{j}) i=1∑mlogP(x(i);θj+1)≥i=1∑mlogP(x(i);θj)
由于
L ( θ , θ j ) = ∑ i = 1 m ∑ z ( i ) P ( z ( i ) ∣ x ( i ) ; θ j ) ) l o g P ( x ( i ) , z ( i ) ; θ ) L(\theta, \theta^{j}) = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)};\theta^{j}))log{P(x^{(i)}, z^{(i)};\theta)} L(θ,θj)=i=1∑mz(i)∑P(z(i)∣x(i);θj))logP(x(i),z(i);θ) 令: H ( θ , θ j ) = ∑ i = 1 m ∑ z ( i ) P ( z ( i ) ∣ x ( i ) ; θ j ) ) l o g P ( z ( i ) ∣ x ( i ) ; θ ) H(\theta, \theta^{j}) = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)};\theta^{j}))log{P( z^{(i)}|x^{(i)};\theta)} H(θ,θj)=i=1∑mz(i)∑P(z(i)∣x(i);θj))logP(z(i)∣x(i);θ)
上两式相减得到:
∑ i = 1 m l o g P ( x ( i ) ; θ ) = L ( θ , θ j ) − H ( θ , θ j ) \sum\limits_{i=1}^m logP(x^{(i)};\theta) = L(\theta, \theta^{j}) - H(\theta, \theta^{j}) i=1∑mlogP(x(i);θ)=L(θ,θj)−H(θ,θj)
在上式中分别取 θ \theta θ 为 θ j 和 θ j + 1 \theta^j和\theta^{j+1} θj和θj+1,并相减得到:
∑ i = 1 m l o g P ( x ( i ) ; θ j + 1 ) − ∑ i = 1 m l o g P ( x ( i ) ; θ j ) = [ L ( θ j + 1 , θ j ) − L ( θ j , θ j ) ] − [ H ( θ j + 1 , θ j ) − H ( θ j , θ j ) ] \sum\limits_{i=1}^m logP(x^{(i)};\theta^{j+1}) - \sum\limits_{i=1}^m logP(x^{(i)};\theta^{j}) = [L(\theta^{j+1}, \theta^{j}) - L(\theta^{j}, \theta^{j}) ] -[H(\theta^{j+1}, \theta^{j}) - H(\theta^{j}, \theta^{j}) ] i=1∑mlogP(x(i);θj+1)−i=1∑mlogP(x(i);θj)=[L(θj+1,θj)−L(θj,θj)]−[H(θj+1,θj)−H(θj,θj)]
要证明EM算法的收敛性,我们只需要证明上式的右边是非负的即可。
由于 θ j + 1 \theta^{j+1} θj+1 使得 L ( θ , θ j ) L(\theta, \theta^{j}) L(θ,θj) 极大,因此有:
L ( θ j + 1 , θ j ) − L ( θ j , θ j ) ≥ 0 L(\theta^{j+1}, \theta^{j}) - L(\theta^{j}, \theta^{j}) \geq 0 L(θj+1,θj)−L(θj,θj)≥0
而对于第二部分,我们有:
H ( θ j + 1 , θ j ) − H ( θ j , θ j ) = ∑ i = 1 m ∑ z ( i ) P ( z ( i ) ∣ x ( i ) ; θ j ) l o g P ( z ( i ) ∣ x ( i ) ; θ j + 1 ) P ( z ( i ) ∣ x ( i ) ; θ j ) ≤ ∑ i = 1 m l o g ( ∑ z ( i ) P ( z ( i ) ∣ x ( i ) ; θ j ) P ( z ( i ) ∣ x ( i ) ; θ j + 1 ) P ( z ( i ) ∣ x ( i ) ; θ j ) ) = ∑ i = 1 m l o g ( ∑ z ( i ) P ( z ( i ) ∣ x ( i ) ; θ j + 1 ) ) = 0 \begin{align} H(\theta^{j+1}, \theta^{j}) - H(\theta^{j}, \theta^{j}) & = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)};\theta^{j})log\frac{P( z^{(i)}|x^{(i)};\theta^{j+1})}{P( z^{(i)}|x^{(i)};\theta^j)} \\ & \leq \sum\limits_{i=1}^mlog(\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)};\theta^{j})\frac{P( z^{(i)}|x^{(i)};\theta^{j+1})}{P( z^{(i)}|x^{(i)};\theta^j)}) \\ & = \sum\limits_{i=1}^mlog(\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)};\theta^{j+1})) = 0 \end{align} H(θj+1,θj)−H(θj,θj)=i=1∑mz(i)∑P(z(i)∣x(i);θj)logP(z(i)∣x(i);θj)P(z(i)∣x(i);θj+1)≤i=1∑mlog(z(i)∑P(z(i)∣x(i);θj)P(z(i)∣x(i);θj)P(z(i)∣x(i);θj+1))=i=1∑mlog(z(i)∑P(z(i)∣x(i);θj+1))=0
其中第(2)式用到了Jensen不等式,只不过和第二节的使用相反而已,第(3)式用到了概率分布累积为1的性质。
至此,我们得到了: ∑ i = 1 m l o g P ( x ( i ) ; θ j + 1 ) − ∑ i = 1 m l o g P ( x ( i ) ; θ j ) ≥ 0 \sum\limits_{i=1}^m logP(x^{(i)};\theta^{j+1}) - \sum\limits_{i=1}^m logP(x^{(i)};\theta^{j}) \geq 0 i=1∑mlogP(x(i);θj+1)−i=1∑mlogP(x(i);θj)≥0, 证明了EM算法的收敛性。
从上面的推导可以看出,EM算法可以保证收敛到一个稳定点,但是却不能保证收敛到全局的极大值点,因此它是局部最优的算法,当然,如果我们的优化目标 L ( θ , θ j ) L(\theta, \theta^{j}) L(θ,θj) 是凸的,则EM算法可以保证收敛到全局最大值,这点和梯度下降法这样的迭代算法相同。至此我们也回答了上面提到的第二个问题。
5. 另一种推导EM算法公式方法
如果我们关心的参数为θ,观察到的数据为y,隐藏变量为z,那么根据全概率公式:
P ( y ∣ θ ) = ∫ P ( y ∣ z , θ ) f ( z ∣ θ ) d z P(y|\theta)=\int P(y|z,\theta)f(z|\theta)dz P(y∣θ)=∫P(y∣z,θ)f(z∣θ)dz
理论上,只要最大化这个密度函数的对数,就可以得到极大似然估计MLE。然而问题是,对z进行积分很多情况下是非常困难的,特别是z的维数可能与样本量一样大,这个时候如果计算数值积分是非常恐怖的一件事情。
而EM算法可以解决这个问题。根据贝叶斯法则,我们可以得到: h ( z ∣ y , θ ) = P ( y ∣ z , θ ) f ( z ∣ θ ) P ( y ∣ θ ) h(z|y,\theta)=\frac{P(y|z,\theta)f(z|\theta)}{P(y|\theta)} h(z∣y,θ)=P(y∣θ)P(y∣z,θ)f(z∣θ)
EM算法的精髓就是使用这个公式处理z的维数问题。
直觉上,EM算法就是一个猜测的过程:给定一个猜测θ’,那么可以根据这个猜测θ’和现实的数据计算隐藏变量取各个值的概率。有了z的概率之后,再根据这个概率计算更有可能的θ。
准确的来说,EM算法就是如下的迭代过程:
θ t + 1 = arg max θ ε ( θ ∣ θ t ) = arg max θ ∫ h ( z ∣ y , θ t ) ln [ P ( y ∣ z , θ ) f ( z ∣ θ ) ] d z \theta_{t+1}=\arg\max_\theta \varepsilon (\theta|\theta_t)=\arg\max_\theta\int h(z|y,\theta_t)\ln[P(y|z,\theta)f(z|\theta)] dz θt+1=argθmaxε(θ∣θt)=argθmax∫h(z∣y,θt)ln[P(y∣z,θ)f(z∣θ)]dz
本节介绍的EM算法是通用的EM算法框架,其实EM算法有很多实现方式,其中比较流行的一种实现方式是高斯混合模型(Gaussian Mixed Model)
三、GMM(Gaussian mixture model) 混合高斯模型(EM算法)
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况。
1. GMM原理
我们已经学习了EM算法的一般形式:
Q i ( z ( i ) ) = P ( z ( i ) ∣ x ( i ) , θ j ) ( 1 ) ∑ z Q i ( z ( i ) ) = 1 L ( θ , θ j ) = ∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ∣ θ ) Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)},\theta^{j})\;\;\;\;(1) \\ \sum\limits_{z}Q_i(z^{(i)}) =1 \\ L(\theta, \theta^{j}) = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)},z^{(i)}|\theta)} Qi(z(i))=P(z(i)∣x(i),θj)(1)z∑Qi(z(i))=1L(θ,θj)=i=1∑mz(i)∑Qi(z(i))logP(x(i),z(i)∣θ) 现在我们用高斯分布来一步一步的完成EM算法。
设有随机变量 X \boldsymbol{X} X,则混合高斯模型可以用下式表示:
p ( x ∣ π , μ , Σ ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) ∑ k = 1 K π k = 1 , 0 < π k < 1 p(\boldsymbol{x}|\boldsymbol{\pi},\boldsymbol{\mu},\boldsymbol{\Sigma})=\sum_{k=1}^K\pi_k\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k) \\ \sum_{k=1}^K\pi_k=1, \ 0<\pi_k<1 p(x∣π,μ,Σ)=k=1∑KπkN(x∣μk,Σk)k=1∑Kπk=1, 0<πk<1
其中 N ( x ∣ μ k , Σ k ) \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) N(x∣μk,Σk) 称为混合模型中的第 k k k 个分量(component)。可以看到 π k \pi_k πk 相当于每个分量 N ( x ∣ μ k , Σ k ) \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) N(x∣μk,Σk) 的权重。
a. 引入隐变量
我们引入一个隐变量 z i k z_{ik} zik, z i k z_{ik} zik的含义是样本 x i x_i xi 来自第 k k k 个模型的数据分布。
z i k = { 1 , i f d a t a i t e m i c o m e s f r o m c o m p o n e n t k 0 , o t h e r w i s e s z_{ik}= \left \{\begin{array}{cc} 1, & if\ data\ item\ i\ comes\ from\ component\ k\\ 0, & otherwises \end{array}\right. zik={1,0,if data item i comes from component kotherwises
则有
P ( x , z ∣ μ k , Σ k ) = ∏ k = 1 K ∏ i = 1 N [ π k N ( x ∣ μ k , Σ k ) ] z i k = ∏ k = 1 K π k n k ∏ i = 1 N [ N ( x ∣ μ k , Σ k ) ] z i k ( 2 ) P(x,z|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) = \prod_{k=1}^K\prod_{i=1}^N[\pi_k\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)]^{z_{ik}}=\prod_{k=1}^K\pi_k^{n_k}\prod_{i=1}^N[\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)]^{z_{ik}}\;\;\;\;(2) P(x,z∣μk,Σk)=k=1∏Ki=1∏N[πkN(x∣μk,Σk)]zik=k=1∏Kπknki=1∏N[N(x∣μk,Σk)]zik(2)
其中 n k = ∑ i = 1 N z i k , ∑ k = 1 K n k = N n_k=\sum\limits_{i=1}^Nz_{ik},\sum\limits_{k=1}^Kn_k=N nk=i=1∑Nzik,k=1∑Knk=N
再对(2)进一步化简得到:
P ( x , z ∣ μ k , Σ k ) = ∏ k = 1 K π k n k ∏ i = 1 N [ 1 2 π Σ k e x p ( − ( x i − μ k ) 2 2 Σ k ) ] z i k P(x,z|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)=\prod_{k=1}^K\pi_k^{n_k}\prod_{i=1}^N[\frac{1}{\sqrt{2\pi}\boldsymbol{\Sigma_k}}exp(-\frac{{(x_i-\boldsymbol{\mu}_k})^2}{2\boldsymbol{\Sigma}_k})]^{z_{ik}} P(x,z∣μk,Σk)=k=1∏Kπknki=1∏N[2πΣk1exp(−2Σk(xi−μk)2)]zik
取对数log后:
l o g P ( x , z ∣ μ k , Σ k ) = ∑ k = 1 K n k l o g π k + ∑ i = 1 N z i k [ l o g ( 1 2 π ) − l o g ( Σ k ) − ( x i − μ k ) 2 2 Σ k ] logP(x,z|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)=\sum_{k=1}^Kn_klog\pi_k+\sum_{i=1}^Nz_{ik}[log(\frac{1}{\sqrt{2\pi}})-log(\boldsymbol{\Sigma_k})-\frac{{(x_i-\boldsymbol{\mu}_k})^2}{2\boldsymbol{\Sigma}_k}] logP(x,z∣μk,Σk)=k=1∑Knklogπk+i=1∑Nzik[log(2π1)−log(Σk)−2Σk(xi−μk)2]
b. 确定E步极大似然函数
计算最大似然估计 L ( θ , θ ( j ) ) L(\theta,\theta^{(j)}) L(θ,θ(j)) , j j j 是第 j j j次EM的过程,下式子中的 E Q E_Q EQ是(1)中 Q Q Q函数的期望值
L ( θ , θ ( j ) ) = E Q [ l o g P ( x , z ∣ μ k , Σ k ) ] L ( θ , θ ( j ) ) = E Q [ ∑ k = 1 K n k l o g π k + ∑ i = 1 N z i k [ D 2 l o g ( 2 π ) − 1 2 l o g ( Σ k ) − ( x i − μ k ) 2 2 Σ k ] ] L ( θ , θ ( j ) ) = ∑ k = 1 K [ ∑ i = 1 N ( E Q ( z i k ) ) l o g π k + ∑ i = 1 N E Q ( z i k ) [ D 2 l o g ( 2 π ) − 1 2 l o g ( Σ k ) − ( x i − μ k ) 2 2 Σ k ] ] L(\theta,\theta^{(j)})=E_Q[logP(x,z|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)] \\ L(\theta,\theta^{(j)})=E_Q[\sum_{k=1}^Kn_klog\pi_k+\sum_{i=1}^Nz_{ik}[\frac{D}{2}log(2\pi)-\frac{1}{2}log(\boldsymbol{\Sigma_k})-\frac{{(x_i-\boldsymbol{\mu}_k})^2} {2\boldsymbol{\Sigma}_k}]] \\ L(\theta,\theta^{(j)})=\sum_{k=1}^K[\sum_{i=1}^N(E_Q(z_{ik}))log\pi_k+\sum_{i=1}^NE_Q(z_{ik})[\frac{D}{2}log(2\pi)-\frac{1}{2}log(\boldsymbol{\Sigma_k})-\frac{{(x_i-\boldsymbol{\mu}_k})^2}{2\boldsymbol{\Sigma}_k}]] L(θ,θ(j))=EQ[logP(x,z∣μk,Σk)]L(θ,θ(j))=EQ[k=1∑Knklogπk+i=1∑Nzik[2Dlog(2π)−21log(Σk)−2Σk(xi−μk)2]]L(θ,θ(j))=k=1∑K[i=1∑N(EQ(zik))logπk+i=1∑NEQ(zik)[2Dlog(2π)−21log(Σk)−2Σk(xi−μk)2]]
我们记 γ i k = E Q ( z i k ) \gamma_{ik}=E_Q(z_{ik}) γik=EQ(zik), n k = ∑ i = 1 N γ i k n_k=\sum\limits_{i=1}^N\gamma_{ik} nk=i=1∑Nγik 可以算出
L ( θ , θ ( j ) ) = ∑ k = 1 K n k [ l o g π k + ( D 2 l o g ( 2 π ) − 1 2 ( l o g ( Σ k ) − ( x i − μ k ) 2 2 Σ k ) ] L(\theta,\theta^{(j)})=\sum_{k=1}^Kn_k[log\pi_k+(\frac{D}{2}log(2\pi)-\frac{1}{2}(log(\boldsymbol{\Sigma_k})-\frac{{(x_i-\boldsymbol{\mu}_k})^2}{2\boldsymbol{\Sigma}_k})] L(θ,θ(j))=k=1∑Knk[logπk+(2Dlog(2π)−21(log(Σk)−2Σk(xi−μk)2)]
因为 D 2 l o g ( 2 π ) \frac{D}{2}log(2\pi) 2Dlog(2π) 是常数,忽略不计
L ( θ , θ ( j ) ) = ∑ k = 1 K n k [ l o g π k − 1 2 ( l o g ( Σ k ) + ( x i − μ k ) 2 Σ k ) ] γ i k = π k N ( x ∣ μ k , Σ k ) ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) L(\theta,\theta^{(j)})=\sum_{k=1}^Kn_k[log\pi_k-\frac{1}{2}(log(\boldsymbol{\Sigma_k})+\frac{{(x_i-\boldsymbol{\mu}_k})^2}{\boldsymbol{\Sigma}_k})] \\ \gamma_{ik}=\frac{\pi_k\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)}{\sum_{k=1}^K\pi_k\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)} L(θ,θ(j))=k=1∑Knk[logπk−21(log(Σk)+Σk(xi−μk)2)]γik=∑k=1KπkN(x∣μk,Σk)πkN(x∣μk,Σk)
c. 确定M步,更新参数
M步的过程是最大 L ( θ , θ j ) L(\theta, \theta^{j}) L(θ,θj),求出 θ ( j + 1 ) \theta^{(j+1)} θ(j+1)
θ j + 1 = a r g max θ L ( θ , θ j ) \theta^{j+1} = arg \max \limits_{\theta}L(\theta, \theta^{j}) θj+1=argθmaxL(θ,θj)
因为有
n k = ∑ i = 1 N γ i k n_k=\sum_{i=1}^N\gamma_{ik} nk=∑i=1Nγik
通过 L ( θ , θ j ) L(\theta, \theta^{j}) L(θ,θj) 对 μ k \mu_k μk, Σ k \Sigma_k Σk 求偏导等于0得到
μ k = 1 n k ∑ i = 1 N γ i k x i \mu_k=\frac{1}{n_k}\sum_{i=1}^N\gamma_{ik}x_i μk=nk1∑i=1Nγikxi
Σ k = 1 n k ∑ i = 1 N γ i k ( x i − μ k ) 2 \Sigma_k=\frac{1}{n_k}\sum_{i=1}^N\gamma_{ik}(x_i-\mu_k)^2 Σk=nk1∑i=1Nγik(xi−μk)2
π k = n k N \pi_k=\frac{n_k}{N} πk=Nnk
2. GMM算法流程
输入:观测数据 x 1 , x 2 , x 3 , . . . , x N x_1,x_2,x_3,...,x_N x1,x2,x3,...,xN
输出:GMM的参数
- 初始化参数
- E步:根据当前模型,计算模型 k k k对 x i x_i xi的影响 γ i k = π k N ( x ∣ μ k , Σ k ) ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) \gamma_{ik}=\frac{\pi_k\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)}{\sum_{k=1}^K\pi_k\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k)} γik=∑k=1KπkN(x∣μk,Σk)πkN(x∣μk,Σk)
- M步:计算 μ k + 1 , Σ k + 1 2 , π k + 1 \mu_{k+1},\Sigma_{k+1}^2,\pi_{k+1} μk+1,Σk+12,πk+1。 n k = ∑ i = 1 N γ i k μ k + 1 = 1 n k ∑ i = 1 N γ i k x i Σ k + 1 2 = 1 n k ∑ i = 1 N γ i k ( x i − μ k ) 2 π k + 1 = n k N n_k=\sum_{i=1}^N\gamma_{ik} \\\mu_{k+1}=\frac{1}{n_k}\sum_{i=1}^N\gamma_{ik}x_i \\ \Sigma_{k+1}^2=\frac{1}{n_k}\sum_{i=1}^N\gamma_{ik}(x_i-\mu_k)^2 \\ \pi_{k+1}=\frac{n_k}{N} nk=i=1∑Nγikμk+1=nk1i=1∑NγikxiΣk+12=nk1i=1∑Nγik(xi−μk)2πk+1=Nnk
- 重复2,3两步直到收敛
References
EM算法数学基础+GMM
EM算法原理总结 -刘建平Pinard
简单实例解释:从似然函数到EM算法(附代码实现)
The EM Algorithm -CMU
https://jingluan-xw.medium.com/binomial-mixture-model-with-expectation-maximum-em-algorithm-feeaf0598b60
https://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html