时间序列预测股票数据—以LSTM模型为例

一、对时间序列的理解：

        时间序列是按照一定时间间隔排列的数据，时间间隔可以是任意时间单位，通过对时间序列的分析，我们可以探寻到其中的现象以及变化规律，并将这些信息用于预测。这就需要一系列的模型，用于将原始时间序列数据放进模型中进行训练，并用训练好的时间序列模型来预测未知的时间序列。

提供的数据：

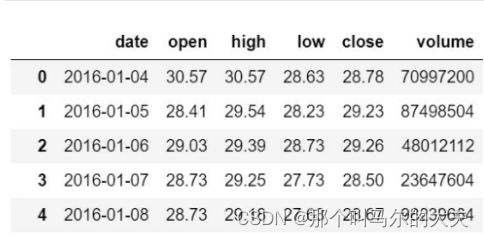
        “中国平安”2016-2018年股票数据，背景为平安保险集团。数据预览如下：

 通过预览数据，可知此次实验的数据属性为date(日期)、open(开盘价)、high(最高价)、low(最低价)、close(收盘价）以及volume(成交量)

        其中，我们要实现股票预测，需要着重对close(收盘价)一列进行探索性分析。

二、使用LSTM进行时序预测

        模型介绍：

        包括遗忘门、输入门、输出门。LSTM将这些卡口作为去除或者增加细胞状态的工具。门是一种让信息选择式通过的方法，他们包含一个sigmoid神经网络层和一个按位的乘法操作。

        其中，每一个sigmoid会输出0到1之间的数值，描述每个部分有多少量可以通过。0表示不允许任何量通过，1表示允许任意量通过。

        LSTM通过三个门，保护和控制细胞状态。

建模思路（包括数据处理、模型分块、建模、模型优化、检验等）

（1）数据处理：

        导入数据，提取数据集的date日期和close收盘价两列，作为建模预测的对象。

        模型分块，设置测试集规模以及滑块大小，现将数据归一化处理，转化为tensor可以识别的数据，再将原数据设定为滑块为1，每调用1批次的数据，将其添加到列表，从而实现二维数据转三维数据，再切分训练集、测试集。

     建模步骤（依据上述思路进行建模，详细描述过程）

        定义网络层：LSTM层（神经元个数：16，激活函数：relu)

        全连接层（神经元个数：1，激活函数：relu，正则化：l2范数）

        模型实例化并装配网络（优化器：采用自适应梯度优化算法Adam，学习率设定为0.1，损失函数采用交叉熵函数，评价指标采用准确率）

        训练模型，设定训练批次为50，每批次样本量为100.

#使用LSTM进行预测
import tensorflow as tf
from tensorflow.keras import datasets, layers, optimizers, Sequential, metrics
from tensorflow.keras.layers import Input,Dropout,Dense,LSTM
from tensorflow.keras.models import Model
from tensorflow.keras import regularizers
import tensorflow.keras as keras
np.random.seed(100)
# 选取随机种子个数100个

        

# 设置神经网络参数
# 提取收盘价
y=stock['close']
print(y)
# 数据预处理
test_ratio=0.4
windows=1
# 设置滑块大小
# 定义测试集规模
# # 通过比例切分
# 测试集大小
from sklearn.preprocessing import MinMaxScaler
data_lsvm=y.values

scaler=MinMaxScaler(feature_range=(0, 1))
data_lsvm=scaler.fit_transform(data_lsvm.reshape(-1,1))



print(data_lsvm)

cut=round(test_ratio* data_lsvm.shape[0])
print(data_lsvm.shape[0])
print('切分：',cut)
train,test=data_lsvm[:data_lsvm.shape[0]-cut,:],data_lsvm[data_lsvm.shape[0]-cut:,:]
amount_of_features=data_lsvm.shape[1]
lstm_input=[]
data_temp=data_lsvm
for i in range(len(data_temp)-windows):

    lstm_input.append(data_lsvm[i:i+windows,:])
lstm_input=np.array(lstm_input)
lstm_output=y[:-windows]

lstm_output=np.array(lstm_output)
x_train,y_train,x_test,y_test=lstm_input[:data_lsvm.shape[0]-cut,:],lstm_output[:data_lsvm.shape[0]-cut],lstm_input[data_lsvm.shape[0]-cut:,:],lstm_output[data_lsvm.shape[0]-cut:]
print(x_train.shape,y_train.shape,x_test.shape,y_test.shape)
x_train

mn_units=16
dropout=0.01
# # 定义网络全连接层
#
def lstm_model():
    inputs=Input(shape=(windows,amount_of_features))

    # lstm层
    rnn = LSTM(units=mn_units, activation='relu',return_sequences=False)(inputs)
    dense=Dropout(dropout)(rnn)
#     dense1=Dense(16,activation='sigmoid',kernel_regularizer=regularizers.l2(0.1))(dense)
#     dense2=Dense(8,activation='relu',kernel_regularizer=regularizers.l2(0.1))(dense)
    outputs=Dense(1,activation='relu',kernel_regularizer=regularizers.l2(0.5))(dense)
    model=Model(inputs=inputs,outputs=outputs)

    model.compile(optimizer=keras.optimizers.Adam(0.1),loss=tf.losses.BinaryCrossentropy(),metrics=['accuracy'])

    model.summary()
    return model
#
batch_size=100
#
epoch=50
# 训练网络
mymodel=lstm_model()
history = mymodel.fit(x_train,y_train,batch_size=batch_size,epochs=epoch)
y_train_predict=mymodel.predict(x_test)

fig= plt.figure(figsize=(8, 5))
plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
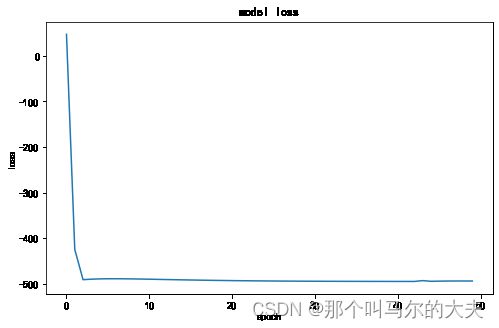
plt.show()

（3）预测结果（数据、拟合图等）

评估结果：

随着训练次数增多，loss值逐渐减小。

将预测后的数据进行评估，并将预测结果反归一化，如图：

# print(mymodel.metrics_names)
loss,acc=mymodel.evaluate(x_test,y_test)
print('评估结果',loss,acc)

y_train_predict=mymodel.predict(x_train)#预测结果
y_test_predict=mymodel.predict(x_test)#预测结果
print('预测结果',y_train_predict,y_test_predict)
print(y_test_predict.shape)

#反归一化


trainPredict=scaler.inverse_transform(y_train_predict)
testPredict = scaler.inverse_transform(y_test_predict)
data_lsvmx=scaler.inverse_transform(data_lsvm)
# y_test = scaler.inverse_transform(y_test)
print(len(trainPredict),len(testPredict))
data_lsvmx

 反归一化后的结果：

# 预测结果

testPredict=pd.DataFrame(testPredict)
close_new=testPredict
close_new.columns=['new_close']
stock_new=stock.iloc[:-windows,:]

# 训练集预测结果
trainPredict=pd.DataFrame(trainPredict)
train_date=stock_new[:data_lsvm.shape[0]-cut].loc[:,['date']]
new_date_train=train_date.reset_index()

new_date_train=new_date_train.drop('index',axis=1)
print(new_date_train)
new_date=stock_new[data_lsvm.shape[0]-cut:].loc[:,['date']]
new_date=new_date.reset_index()
new_date=new_date.drop('index',axis=1)
# date=pd.concat([new_date_train,new_date],axis=0)
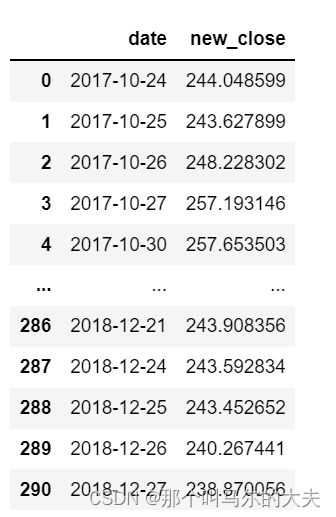
new_predict=pd.concat([new_date,close_new],axis=1)

新的预测结果：

 作图：

# 构建通过训练集进行预测的图表数据
predict_train_plot = np.empty_like(data_lsvm)
predict_train_plot[:, :] = np.nan
predict_train_plot[:data_lsvm.shape[0]-cut, :] = trainPredict
# 构建通过测试集进行预测的图表数据
predict_test_plot = np.empty_like(data_lsvm)
predict_test_plot[:, :] = np.nan
predict_test_plot[data_lsvmx.shape[0]-cut+1:, :] = testPredict

# 原数据
data_plot = np.empty_like(data_lsvmx)
data_plot[:, :] = np.nan
data_plot[:, :] = data_lsvmx

# # 构建通过原数据进行拟合的图表数据
date=stock.loc[:,['date']]
type(date["date"])

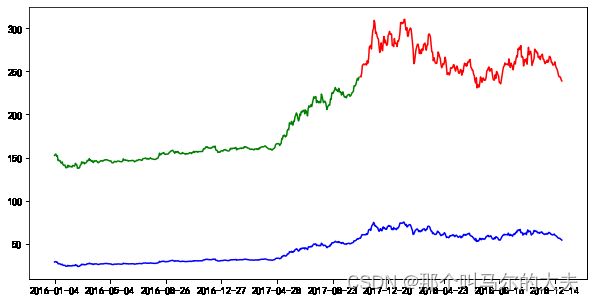
最后绘制预测图：

fig2 = plt.figure(figsize=(10, 5))
dataset = scaler.inverse_transform(data_lsvm)
plt.plot(date["date"],predict_train_plot, color='green')
plt.plot(date["date"],predict_test_plot, color='red')
plt.plot(date["date"],data_plot, color='blue')
plt.xticks(range(0,730,80))
plt.show()

         通过构建训练集进行预测的图表数据和通过测试集进行预测的图表数据，以及原数据的图表数据。

        由图可知，该模型预测的价格走势和原数据走势大体吻合。