算法通关村 | 第一关 | 青铜小白篇
从头开始了解链表
什么是链表?
链表(LinkedList)是一种常见的数据结构,用于存储和组织数据。它由一系列节点(Node)组成,每个节点包含数据元素和一个指向下一个节点的引用(指针或链接)。
链表中的节点在内存中可以分散存储,每个节点通过指针连接到下一个节点,从而形成一个链式结构。
相比于数组等连续存储结构,链表的插入、删除操作一般情况下更加高效,因为它不需要进行元素的移动。
链表的分类
链表可以分为单向链表和双向链表两种类型:
单向链表(Singly Linked List):每个节点只有一个指向下一个节点的指针。最后一个节点指向空(null),表示链表的结束。
双向链表(Doubly Linked List):每个节点有两个指针,一个指向前一个节点,一个指向后一个节点。双向链表可以从头到尾或从尾到头遍历。
简单了解了什么是链表,接下来我们就要深入交流一下具体的细节和实现:
算法的基础是数据结构,任何数据结构的基础都是创建 + 增删改查。
先从单向链表说起吧
单链表基础与构造方法
当我们谈论单链表时,可以将其比作一列相连的火车车厢,每个车厢都代表一个节点,节点之间通过连接来组成一个链表。
现在,假设我们有一个单链表,其中包含三个节点,分别是节点A、节点B和节点C。每个节点都有两个重要的部分:数据(例如整数、字符串等)和指向下一个节点的引用。
我们将节点A想象成第一个车厢,它包含了一些数据并且指向下一个节点,也就是节点B,就像是第一个车厢连接着第二个车厢。节点B也有自己的数据和指向下一个节点的引用,它指向了节点C。最后,节点C是最后一个车厢,它的引用指向空值,表示链表的结束。
节点A 节点B 节点C
+------+ +------+ +------+
| data | | data | | data |
+------+ +------+ +------+
| next |-->| next |-->| null |
+------+ +------+ +------+
在这个链表中,我们可以从头节点(节点A)开始,沿着每个节点的next引用依次访问下一个节点,直到最后一个节点。
单链表的特点是它只允许从头到尾的单向遍历,也就是只能从前往后遍历节点,而无法反向或跳跃遍历。此外,我们可以通过修改节点的next引用来插入、删除或重新排列节点,而不需要像数组一样进行元素的移动。
除此之外,我们还要了解 JVM 是如何构建出链表的,我们应该都知道JVM里有栈区和堆区,栈主要存引用,即一个指向实际对象的地址,堆区才是存放创建对象的区域,比如我们定义了一个如下的类:
public class Course{
Teacher teacher;
Student student;
// 其中teacher和student就是栈中指向堆的引用
}如果我们再定义一个类如下:
class Node {
int data;
Node next;
public Node(int data) {
this.data = data;
this.next = null;
}
}
在Java中,当我们创建一个对象时,实际的对象实例会被分配在堆(Heap)内存中,而栈(Stack)内存中存储了对对象的引用。
例如,当我们执行以下代码时:
Node node = new Node(1);首先,在堆内存中分配了一个新的 Node 对象,其中data属性被设置为1,并且next属性被设置为null。然后,创建的Node对象的地址(引用)会被存储在栈内存中的node变量中。
栈内存: node -> 地址1
堆内存: 地址1 -> Node对象:data = 1, next = null这样,我们就在堆内存中创建了一个Node对象,并且通过栈内存中的引用变量node来引用它。
当我们在链表中连接多个节点时,实际上是通过将前一个节点的next属性指向下一个节点的引用来建立节点之间的链接。
例如,如果我们创建了一个简单的链表:
Node head = new Node(1);
Node second = new Node(2);
Node third = new Node(3);
head.next = second;
second.next = third; 在这个例子中,我们创建了三个 Node对象,并使用引用变量将它们链接起来。head节点的next属性指向second节点,而second节点的next属性指向third节点。
栈内存:
head -> 地址1
second -> 地址2
third -> 地址3
堆内存:
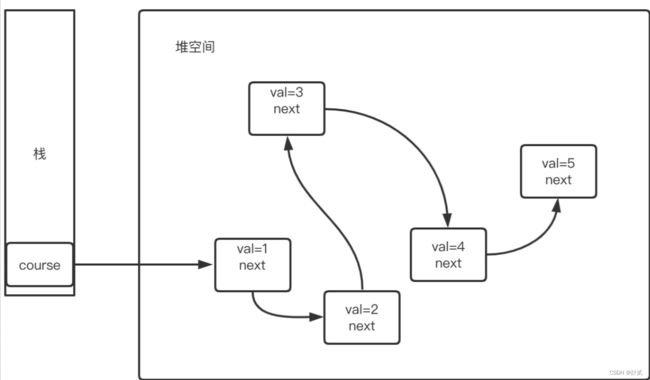
地址1 -> Node对象:data = 1, next -> 地址2
地址2 -> Node对象:data = 2, next -> 地址3
地址3 -> Node对象:data = 3, next = null通过这种方式,我们在堆内存中创建了一个链表,每个节点都有自己的数据和指向下一个节点的引用。
在图中可表示为:
在 IDEA 中 debug 执行的结果如下:
这就是一个简单的单链表线性结构示例,从head开始,逐步向后访问。
遍历链表
遍历链表可以使用循环和递归 但不管使用什么方法,都是从头开始向后遍历,所以这个 “头” 是非常重要的,我们不能一个劲儿的往后遍历,要记录当前的头。
// 使用循环
Node current = head; // 假设head是链表的头节点
while (current != null) {
// 访问或操作当前节点的数据
System.out.println(current.data);
// 将当前节点更新为下一个节点
current = current.next;
}
// 使用递归
public void traverse(Node node) {
if (node == null) {
return; // 递归终止条件:当前节点为null
}
// 访问或操作当前节点的数据
System.out.println(node.data);
// 递归调用函数,传递当前节点的下一个节点
traverse(node.next);
}
// 调用遍历函数,从头节点开始
traverse(head); // 假设head是链表的头节点
链表插入
单向链表的插入和数组的插入相似,但又分为头部、尾部和中间插入。
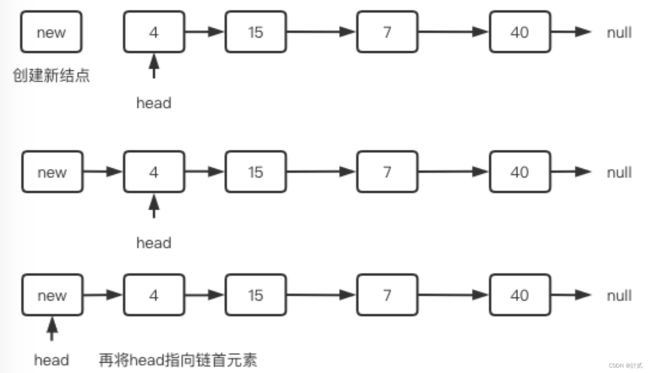
- 头部插入:创建一个新结点 Node ,执行Node.next = head,再把Node赋值给head即可。(head = Node)
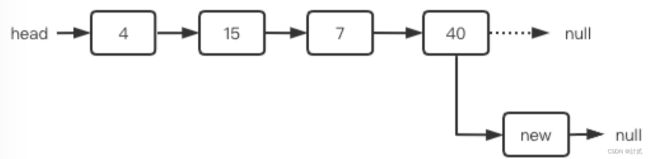
- 尾部插入:将尾结点指向新结点即可。
- 中间插入:
当我们在单链表中进行中间插入时,可以将其比作在火车车厢之间插入一个新的车厢。这涉及到更改相邻车厢之间的链接。
让我们通过以下示例来生动讲解一下单链表的中间插入操作:
假设我们有一个单链表,其中包含三个节点,分别是节点A、节点B和节点C。我们希望在节点B之后插入一个新的节点。
初始链表状态:
节点A 节点B 节点C
+------+ +------+ +------+
| data | | data | | data |
+------+ +------+ +------+
| next |-->| next |-->| null |
+------+ +------+ +------+
现在,我们要在节点B之后插入一个新的节点,比如节点D。首先,我们创建一个新节点D,并为其设置数据。
接下来,我们需要更改节点B和节点C之间的链接。我们将新节点D的next指针指向节点C,然后将节点B的next指针指向节点D。
更新链接:
节点A 节点B 节点D 节点C
+------+ +------+ +------+ +------+
| data | | data | | data | | data |
+------+ +------+ +------+ +------+
| next |-->| next |-->| next |-->| null |
+------+ +------+ +------+ +------+
然后我们就成功地在节点B之后插入了新的节点D。节点D的链接与相邻节点建立了正确的关系,链表结构得到了更新。
综上单链表的插入代码可如下:
// head 链表头节点
// nodeInsert 待插入节点
// position 待插入位置,从1开始
public static Node insertNode(Node head, Node nodeInsert, int position) {
if (head == null) {
//这里可以认为待插入的结点就是链表的头结点,也可以抛出不能插入的异常
return nodeInsert;
}
//已经存放的元素个数
int size = getLength(head);
if (position > size+1 || position < 1) {
System.out.println("位置参数越界");
return head;
}
//表头插入
if (position == 1) {
nodeInsert.next = head;
// 这里可以直接 return nodeInsert;还可以这么写:
head = nodeInsert;
return head;
}
Node pNode = head;
int count = 1;
//这里position被上面的size被限制住了,不用考虑pNode=null
while (count < position - 1) {
pNode = pNode.next;
count++;
}
nodeInsert.next = pNode.next;
pNode.next = nodeInsert;
return head;
}链表删除
删除和插入类类似,原理部分就不再赘述了,代码如下:
简单说完了单向链表,接下来趁热打铁,继续学习一下双向链表吧!
双向链表的基础与设计
双向链表(Doubly Linked List)是一种常见的数据结构,与单向链表相比,它的每个节点除了包含数据元素外,还有两个指针(引用):一个指向前一个节点,一个指向后一个节点。
双向链表的基本概念包括以下几个要点:
- 节点结构:每个节点由数据元素和两个指针组成。通常,我们将其定义为一个类,类中包含数据和两个指针的实例变量。
class Node { int data; Node prev; // 前一个节点的引用 Node next; // 后一个节点的引用 public Node(int data) { this.data = data; this.prev = null; this.next = null; } }
- 链表结构:双向链表由多个节点组成,每个节点通过前一个节点的引用和后一个节点的引用链接起来。
class DoublyLinkedList { Node head; // 头节点 // 构造方法等其他操作 // ... }
双向遍历:双向链表可以从头到尾或从尾到头进行双向遍历。我们可以根据需要,从头节点或尾节点开始遍历链表,然后通过前一个节点和后一个节点的引用来访问相邻的节点。
插入和删除操作:双向链表相对于单向链表在插入和删除操作上更加灵活。通过前一个节点和后一个节点的引用,我们可以方便地在任意位置插入新节点或删除现有节点。
双向链表的两种遍历方式(从前往后 | 从后往前):
class Node {
int data;
Node prev;
Node next;
public Node(int data) {
this.data = data;
this.prev = null;
this.next = null;
}
}
class DoublyLinkedList {
Node head;
Node tail;
// 在构造函数等其他操作
// ...
// 从头到尾遍历
public void traverseForward() {
Node current = head;
while (current != null) {
// 访问或操作当前节点的数据
System.out.println(current.data);
// 将当前节点更新为下一个节点
current = current.next;
}
}
// 从尾到头遍历
public void traverseBackward() {
Node current = tail;
while (current != null) {
// 访问或操作当前节点的数据
System.out.println(current.data);
// 将当前节点更新为前一个节点
current = current.prev;
}
}
}
TODO 双向链表的插入和删除之后会陆续补充!!!!
补充来了dog
双向链表的插入
操作双向链表相比于单向链表麻烦一点,但也分为头、中和尾部插入,具体的会在以下代码中有所体现:
// 以下代码是头和尾的插入
class DoubleNode {
int data;
DoubleNode prev;
DoubleNode next;
public DoubleNode(int data) {
this.data = data;
this.prev = null;
this.next = null;
}
}
class DoublyLinkedList {
DoubleNode first;
DoubleNode last;
// 构造函数和其他方法...
// 头部插入
public void insertFirst(int data) {
DoubleNode newDoubleNode = new DoubleNode(data);
if (isEmpty()) {
last = newDoubleNode;
} else {
// 如果不是第一个节点的情况
// 将还没插入新节点之前链表的第一个节点的previous指向newNode
first.prev = newDoubleNode;
newDoubleNode.next = first;
}
// 将新节点赋给first,成为第一个节点
first = newDoubleNode;
}
// 尾部插入
public void insertLast(int data) {
DoubleNode newDoubleNode = new DoubleNode(data);
if (isEmpty()) {
first = newDoubleNode;
} else {
newDoubleNode.prev = last;
last.next = newDoubleNode;
}
// 由于插入了一个新的节点,将last指向newNode
last = newDoubleNode;
}
private boolean isEmpty() {
return (first == null);
}
}
中间插入有所不同,具体流程和代码如下:
// 中间插入
public void insertAfter(int key, int data) {
DoubleNode newNode = new DoubleNode(data);
DoubleNode current = first;
// 寻找key值对应的节点
while (current != null && current.data != key) {
current = current.next;
}
// 若找不到key值对应的节点
if (current == null) {
if (isEmpty()) {
first = newNode;
last = newNode;
} else {
// 在链表尾部插入一个新节点
last.next = newNode;
newNode.prev = last;
last = newNode;
}
} else {
// 找到了key值对应的节点,分两种情况
if (current == last) {
// key值与最后一个节点的data相等
newNode.next = null;
last = newNode;
} else {
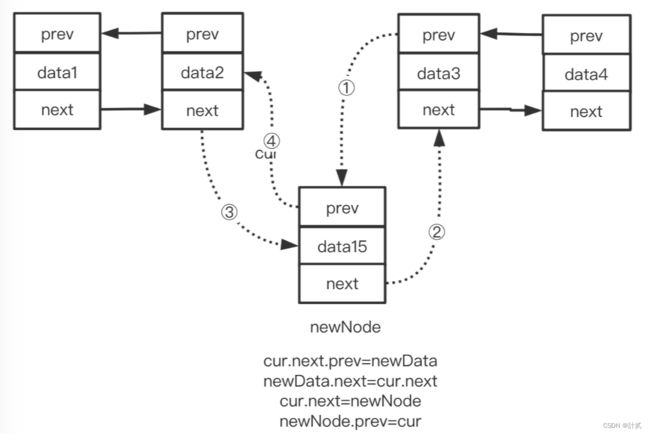
// 在两个节点之间插入新节点
newNode.next = current.next;
current.next.prev = newNode;
}
current.next = newNode;
newNode.prev = current;
}
}
删除结点
双向链表的删除和插入相似,话不多说直接上代码:
// 删除首或尾
public DoubleNode deleteFirst() {
DoubleNode temp = first;
// 若链表只有一个结点,删除后链表为空,将last指向null
if (first.next == null) {
last = null;
} else {
// 若链表有两个及以上的结点,因为是头部删除,则first.next将变成第一个结点,其prev将为null
first.next.prev = null;
}
// 将first.next赋给first
first = first.next;
// 返回删除的结点
return temp;
}
public DoubleNode deleteLast() {
DoubleNode temp = last;
// 如果链表只有一个结点,则删除以后为空表,last指向null
if (first.next == null) {
first = null;
} else {
// 将上一个结点的next域指向null
last.prev.next = null;
}
// 上一个结点成为最后一个结点,last指向它
last = last.prev;
// 返回删除的结点
return temp;
}
删除中间的元素:
public DoubleNode deleteKey(int key) {
DoubleNode current = first;
// 遍历链表寻找该值所在的结点
while (current != null && current.data != key) {
current = current.next;
}
// 若当前结点指向null,则返回null
if (current == null) {
return null;
} else {
// 如果current是第一个结点
if (current == first) {
// 将first指向它,将该结点的prev指向null,其余不变
first = current.next;
current.next.prev = null;
} else if (current == last) {
// 如果current是最后一个结点
last = current.prev;
current.prev.next = null;
} else {
// 当前结点的上一个结点的next域应指向当前的下一个结点
current.prev.next = current.next;
// 当前结点的下一个结点的prev域应指向当前结点的上一个结点
current.next.prev = current.prev;
}
return current;
}
}