算法训练day2有序数组的平方 长度最小的子数组 螺旋矩阵II

有序数组的平方

Category	Difficulty	Likes	Dislikes	ContestSlug	ProblemIndex	Score
algorithms	Easy (68.33%)	749	0	weekly-contest-120	Q1	1129

Tags

Companies

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 已按 非递减顺序 排序

进阶：

• 请你设计时间复杂度为 O(n) 的算法解决本问题

暴力题解

class Solution {
public:
    
int partition(vector& nums, int left, int right) {
	// 选取基准值
	int pivot = nums[left];
	int i = left, j = right;
	while (i < j) {
		// 移动 j
		while (i < j && nums[j] >= pivot) {   // 1 2 3 4 5 6 7 8 9
			j--;
		}
		// i == j || arr[j] < pivot
		nums[i] = nums[j];

		// 移动 i
		while (i < j && nums[i] <= pivot) {
			i++;
		}
		// i == j || arr[i] > pivot
		nums[j] = nums[i];
	}
	// i == j
	nums[i] = pivot;
	return i;
}

void quick_sort1(vector& nums, int left, int right) {
	// 边界条件
	if (left >= right) return;
	// 递归公式
	int idx = partition(nums, left, right);
	quick_sort1(nums, left, idx - 1);
	quick_sort1(nums, idx + 1, right);
}
void quick_sort(vector& nums) {
	quick_sort1(nums, 0, nums.size()-1);
}
    
    
    vector sortedSquares(vector& nums) {

        for(int i = 0; i < nums.size();++i){
            nums[i] *=nums[i]; 
        }
		quick_sort(nums);//快排
		
		return nums;
    }
};

双指针

数组其实是有序的， 只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，right指向起始位置，left指向终止位置。

class Solution {
public:
    vector sortedSquares(vector& nums) {
		int size = nums.size()-1;
		vector result(nums.size(), 0);
		int left = 0 , right = size; 
		while(left <= right) {
			if(nums[left]*nums[left] > nums[right]* nums[right]) {
				result[size--] = nums[left] * nums[left];
				left++;
			}else{
				result[size--] = nums[right] * nums[right];
				right--;
			}
		}
		return result;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

长度最小的子数组

Category	Difficulty	Likes	Dislikes	ContestSlug	ProblemIndex	Score
algorithms	Medium (47.19%)	1612	0	-	-	0

Tags

Companies

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

进阶：

• 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

---

Discussion | Solution

滑动窗口题解（本质还是双指针）

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考 如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入 暴力解法的怪圈。

所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {

        int result = INT32_MAX;
        int sum = 0;
        int i = 0 ;
        int subLength = 0;
        for(int j = 0; j < nums.size(); ++j) {

            sum += nums[j];
            while(sum >= target) {

                subLength = j-i+1;

                result = result < subLength ? result : subLength;
                
                sum -= nums[i++];
            } 
            
        }
        return result == INT32_MAX ? 0 : result;

    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

螺旋矩阵 II

Category	Difficulty	Likes	Dislikes	ContestSlug	ProblemIndex	Score
algorithms	Medium (73.72%)	979	0	-	-	0

Tags

Companies

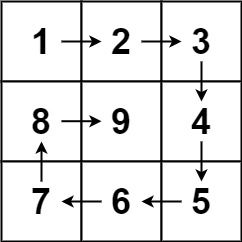
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

---

Discussion | Solution

题解(重点找到循环不变式)

class Solution {
public:
    vector> generateMatrix(int n) {
        vector> res(n,vector(n,0));
        int startx = 0, starty = 0;
        int loop = n / 2;
        int mid = n / 2;
        int count = 1;
        int offset = 1;
        int i,j;
        while(loop--) {
            i = startx;
            j = starty;
            for(;j < n - offset; ++j) {
                res[startx][j] = count++;
            }
            for(;i < n - offset; ++i) {
                res[i][j] = count++;
            }
            for(;j > starty; --j) {
                res[i][j] = count++;
                
            }
            for(;i > startx; --i) {
                res[i][j] = count++;
            }
            if(n%2) {
                res[mid][mid] = count;
            }
            startx++;
            starty++;
            offset++;
        }
        if(n%2) {
                res[mid][mid] = count;
        }
        return res;
    }
};

[本文参考链接：](代码随想录 (programmercarl.com))

        res[mid][mid] = count;
        }
        startx++;
        starty++;
        offset++;
    }
    if(n%2) {
            res[mid][mid] = count;
    }
    return res;
}

};

[原文链接](https://github.com/1750252467/CppLearning/blob/main/LeetCode/Day2/%E7%AE%97%E6%B3%95%E8%AE%AD%E7%BB%83day2.md)
[本文参考链接：]([代码随想录 (programmercarl.com)](https://programmercarl.com/0977.有序数组的平方.html))