浅谈lowbit运算
今天一起来简单了解一下lowbit()运算,小白技术水平有限,只是简单介绍一下,欢迎大佬指教!
介绍
首先来简单介绍一下lowbit(),lowbit(x)的值是x的二进制表达式中最低位的1所对应的十进制值。通俗点来说,lowbit(x)是将 x 转化成二进制数之后,只保留最低位(从右往左数,第一位)的1及其后面的0,截断前面的内容,然后再转成10进制数。
举个列子,lowbit(6) = 2,lowbit(7) = 1
| 原数 | 二进制 | lowbit(x) |
|---|---|---|
| 6 | 110 | 21 = 2 |
| 7 | 111 | 20 = 1 |
原理(可能讲解的很不到位,甚至出错,欢迎大佬指教)
- x=1,lowbit(1) = 1;
(原码与补码的转换,小伙伴们可以自行了解一下啊)
| 原数 | 原码/补码 |
|---|---|
| 1 | 0000 0001 |
| -1 | 1111 1111 |
0 0 0 0 0 0 0 1
& 1 1 1 1 1 1 1 1
————————————————————————
= 0 0 0 0 0 0 0 1
lowbit(1) = 20 = 1;
- x=6,lowbit(6) = 2;
| 原数 | 原码/补码 |
|---|---|
| 6 | 0000 0110 |
| -6 | 1111 1010 |
0 0 0 0 0 1 1 0
& 1 1 1 1 1 0 1 0
————————————————————————
= 0 0 0 0 0 0 1 0
lowbit(6) = 21 = 2;
总结
lowbit(x)=2p(p是指将x转化为二进制之后从右往左数第一个1的位置)
比如1的二进制写作0000001,1处于第0位,所以p=0, 20=1, 所以lowbit(1)=1;
比如6的二进制写作0000110,1处于第1位,所以p=1, 21=2, 所以lowbit(6)=2。
lowbit函数的实现方式
首先,先简单介绍一下两种运算:^运算(异或运算)与 &运算(与运算):
^运算(异或运算)
运算规则:
0^0=0; 0^1=1; 1^0=1; 1^1=0;
&运算(与运算)
运算规则:
0&0=0;0&1=0;1&0=0;1&1=1
lowbit函数实现方式一:
x&-x
下面是两个简单的列子(小伙伴们可以参考一下):
1. x=1,lowbit(1) = 1;
(原码与补码的转换,小伙伴们可以自行了解一下啊)
| 原数 | 原码/补码 |
|---|---|
| 1 | 0000 0001 |
| -1 | 1111 1111 |
0 0 0 0 0 0 0 1
& 1 1 1 1 1 1 1 1
————————————————————————
= 0 0 0 0 0 0 0 1
lowbit(1) = 20 = 1;
2. x=6,lowbit(6) = 2;
| 原数 | 原码/补码 |
|---|---|
| 6 | 0000 0110 |
| -6 | 1111 1010 |
0 0 0 0 0 1 1 0
& 1 1 1 1 1 0 1 0
————————————————————————
= 0 0 0 0 0 0 1 0
lowbit(6) = 21 = 2;
lowbit函数实现方式二:
x&(x^(x-1))
下面举两个例子,来简单说明一下:
1. x=1,lowbit(1) = 1;
| 原数 | 原码/补码 | x-1 |
|---|---|---|
| 1 | 0000 0001 | 0000 0000 |
第一步
x-1可以直接按照二进制减法,或者转化为x+(-1)
按照减法做:
1 的原码:0000 0001
0 0 0 0 0 0 0 1
- 0 0 0 0 0 0 0 1
————————————————————————
= 0 0 0 0 0 0 0 0
按照加法做:x+(-1)
-1 的补码:1111 1111
0 0 0 0 0 0 0 1
+ 1 1 1 1 1 1 1 1
————————————————————————
= 0 0 0 0 0 0 0 0
总之,x-1 = (1)2 - (1)2 = (0)2
接下来,进行下一步运算:x^(x-1)
第二步
x^(x-1) :
0 0 0 0 0 0 0 1
^ 0 0 0 0 0 0 0 0
————————————————————————
= 0 0 0 0 0 0 0 1
x^(x-1) = (0000 0001)(二进制表示)
x&(x^(x-1))
第三步
x&(x^(x-1)) :
0 0 0 0 0 0 0 1
& 0 0 0 0 0 0 0 1
————————————————————————
= 0 0 0 0 0 0 0 1
综上三步所述,lowbit(1) = 20 = 1;
2. x=6,lowbit(6) = 2;
| 原数 | 原码/补码 | x-1 |
|---|---|---|
| 6 | 0000 0110 | 0000 0101 |
第一步
x-1可以直接按照二进制减法,或者转化为x+(-1)
按照减法做:
6 的原码:0000 0110
0 0 0 0 0 1 1 0
- 0 0 0 0 0 0 0 1
————————————————————————
= 0 0 0 0 0 1 0 1
按照加法做:x+(-1)
-1 的补码:1111 1111
0 0 0 0 0 1 1 0
+ 1 1 1 1 1 1 1 1
————————————————————————
= 0 0 0 0 0 1 0 1
总之,x-1 = (6)2 - (1)2 = (5)2
接下来,进行下一步运算:x^(x-1)
第二步
x^(x-1) :
0 0 0 0 0 1 1 0
^ 0 0 0 0 0 1 0 1
————————————————————————
= 0 0 0 0 0 0 1 1
x^(x-1) = (0000 0011)(二进制表示)
x&(x^(x-1))
第三步
x&(x^(x-1)) :
0 0 0 0 0 1 1 0
& 0 0 0 0 0 0 1 1
————————————————————————
= 0 0 0 0 0 0 1 0
综上三步所述,lowbit(6) = 21 = 2;
使用lowbit运算统计二进制数中1的个数
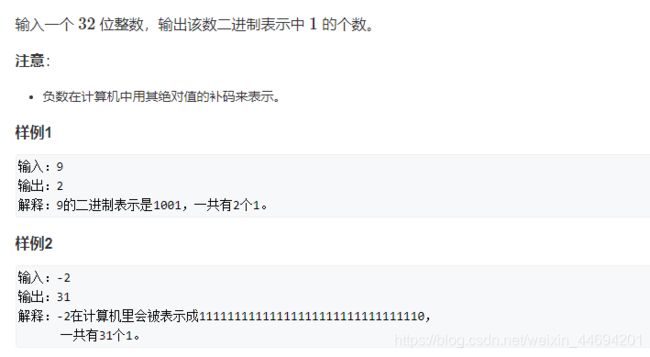
这个题是最近做到的一个题目,运用的技术就是使用lowbit运算:
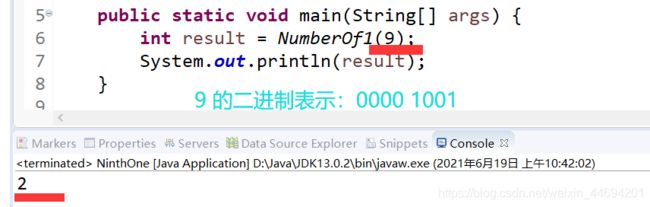
public class NinthOne {
public static void main(String[] args) {
int result = NumberOf1(9);
System.out.println(result);
}
public static int NumberOf1(int n)
{
int result = 0;
while(n!=0) {
// 两种方法求lowbit的值都可以:n&-n 或者 n&(n^(n-1))
// n = n - (n & -n);
n = n- (n & (n ^ (n - 1)));
result++;
}
return result;
}
}

本小白技术有限,lowbit 在树状数组 等问题中也有很多应用,欢迎大佬可以指教,也欢迎小伙伴们可以一起探讨,一起加油!
