JS：二叉搜索树（1）——中序遍历，基础操作

Binary Search Tree
简单总结下吧，BST 相关的问题，要么利用 BST 左小右大的特性提升算法效率，要么利用中序遍历的特性满足题目的要求，也就这么些事儿吧。

230. 二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

BST 的中序遍历其实就是升序排序的结果

var kthSmallest = function(root, k) {
    let res = 0, rank = 0;
    function traverse(root) {
        if(root == null) return
        traverse(root.left)
        rank++;
        if(rank == k) {
            res = root.val
            return
        }
        traverse(root.right)
    }
    traverse(root)
    return res
};

538. 把二叉搜索树转换为累加树 （中等）

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值 等于 原树中大于或等于 node.val 的值之和。

观察下图，值的大小与原来相反

明显利用中序遍历的相反方式：右跟左，就是逆序排列
一开始就想到左节点怎么拿到父亲节点这个问题，但由于是累加的关系，节点的值是逐渐增大大的，所以可以用全局变量来记录。就变成了简单的遍历问题。

var convertBST = function(root) {
    let sum = 0
    function build(root) {
        if(root == null) return
        build(root.right)
        sum += root.val
        root.val = sum
        build(root.left)
    }
    build(root)
    return root
};

---

手把手带你刷二叉搜索树（第二期）
本文来实现 BST 的基础操作：判断 BST 的合法性、增、删、查。其中「删」和「判断合法性」略微复杂。

98. 验证二叉搜索树 （中等） fail

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

需要注意：

方法：通过使用辅助函数，增加函数参数列表，在参数中携带额外信息，将这种约束传递给子树的所有节点

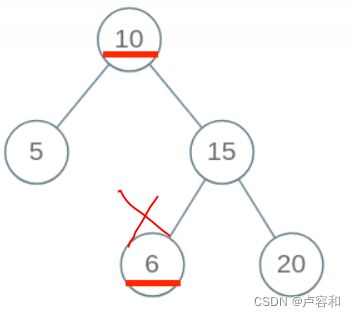
只关注当前根节点，
第一，验证根节点是否符合父亲给他的规范——在【min，max】区间中。初始情况，肯定没有大小限制。

第二，当前根节点对他的左孩子的要求：min最小值——没有约束，即不变。max最大值要小于自己root.val。
不变的意思是：可能当前根节点的父亲有min最小值的约束，比如上述的6，它的最小值10是父亲的父亲来规定的。

有人疑惑，这个10的规定是怎么传给了6的呢？在看当前根节点对他的右孩子的要求：min最小值要大于直接root.val。看出来是从这时要去的。max最大值就没有约束，也是不变。

有人可能像我一样，质疑这样就能满足全部的状况吗？之前提过，我们不要去脑补递归。我们可以随便选一个根节点，处理好当前节点，和函数应该对下一层递归做好什么约束就可以了。

写这么多也是为了理解，背递归代码是没有用的。

边界问题：
[2,2,2]
预期结果：false
所以是开区间

如果没有约束，我们初始化min和max为null，后面就判断是否为null来确定有无约束

function check(root, min, max) {
    if(root == null) return true
    if(min!=null && root.val <= min) return false
    if(max!=null && root.val >= max) return false
    return check(root.left, min, root.val) && check(root.right, root.val, max)
}

var isValidBST = function(root) {
    return check(root, null, null)
};

700. 二叉搜索树中的搜索 （简单）

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

var searchBST = function(root, val) {
    if(root == null) return null
    if(root.val == val) return root
    if(root.val < val){
        return searchBST(root.right, val)
    } else {
        return searchBST(root.left, val)
    }
};

701. 二叉搜索树中的插入操作 （中等）fail递归

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

一旦涉及「改」，函数就要返回 TreeNode 类型，并且对递归调用的返回值进行接收。

二叉树的查找，只会从上到下走一次，走到最后就是插入的位置。
递归代码：

var insertIntoBST = function(root, val) {
    if(root == null) return new TreeNode(val)
    if(root.val < val){
        root.right = insertIntoBST(root.right, val)
    } else {
        root.left = insertIntoBST(root.left, val)
    }
    return root // 最后要求返回根节点
};

也可以先找到最后一个非空节点，这就是迭代。

var insertIntoBST = function(root, val) {
    if(root == null) return new TreeNode(val)
    let node = root, fa = null
    while (node) {
        if(node.val<val){
            fa = node
            node = node.right
        }else if(node.val>val) {
            fa = node
            node = node.left
        }
    }
    let child = new TreeNode(val)
    fa.val < val ? fa.right=child : fa.left=child
    return root // 最后要求返回根节点
};

450. 删除二叉搜索树中的节点 （中等）

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：
首先找到需要删除的节点；
如果找到了，删除它。

没做之前也知道要分情况：试着自己列举一下
1.删除的是子节点。直接删除
2.删除的节点只有一个分支。直接让这个分支的根节点代替自己。
3.删除的节点两边都有分支。找左子树的最右边节点代替自己，或者找右子树的最左边。

习惯一下对递归调用的返回值进行接收。 递归函数的含义：修改过后的子树
写代码时要分清当前的root是指哪一个

function del(root) {
    if(root.left==null && root.right==null) return null
    if(root.left==null || root.right==null) return root.left? root.left : root.right
    let min = root.right
    while(min.left) min = min.left;
    // 先删除右子树最小的节点
    root.right = deleteNode(root.right, min.val)
    // 用右子树最小的节点替换 root 节点
    min.left = root.left
    min.right = root.right
    return min
}
var deleteNode = function(root, key) {
    if(root == null) return null
    if(root.val == key){
        root = del(root)
    } else if(root.val < key){
        root.right = deleteNode(root.right, key)
    } else{
        root.left = deleteNode(root.left, key)
    }
    return root
};