【每日一题】参加会议的最多员工数

Tag

【内向基环树+拓扑排序+分类讨论】【图】【2023-11-01】

---

题目来源

2127. 参加会议的最多员工数

---

题目解读

员工只有坐在自己喜欢的员工旁边才会参加会议，请问参加会议的最多员工数。

---

解题思路

方法一：内向基环树+拓扑排序+分类讨论

内向基环树

有 k 个点和 k 条边的有向图必定有且仅有一个环，这样的有向图叫做内向基环树。 内向基环树中的环被称为基环，一个单独的环也可以被称为基环。内向基环树通常由一个基环和其余指向基环的树枝组成。一棵典型的内向基环树如下图所示：

图中的蓝色节点表示基环上的节点，绿色节点表示树枝上的节点。

题目中给定的员工之间的座位要求（每个员工必须坐在喜欢的员工旁边），如果我们把员工看成是图上的一个节点，如果员工 x 喜欢员工 y，就在从 x 对应的节点到 y 对应的节点之间连一条边，那么形成的就是由若干颗内向基环树组成的图。按照上述员工之间的连接规则，示例 3 构成的图为：

分类讨论

明确了员工之间的内向基环树关系之后，接下来需要对基环长度进行讨论（因为不同的基环长度对结果会产生明显的区别），有以下两种情况：

• 基环长度大于 2；
• 基环长度等于 2；
• 没有其他情况了，基环的长度最小为 2。

基环长度大于 2

先来看一下基环长度大于 2 的情况，该情况下树枝是无法插入到基环中两个节点之间的。因为，树枝上的点若插入圆桌上 x→y 这两人中间，会导致节点 x 无法和其喜欢的员工坐在一起。此外，树枝上的点也不能单独组成圆桌，因为这样会存在一个出度为 0 的节点，无法和其喜欢的员工坐在一起。

因此，对于基环长度大于 2 的情况，圆桌的最大员工数目即为最大的基环长度，记作 maxRingSize。

基环长度等于 2

基环树的长度为 2 时，比如下面这种情况：

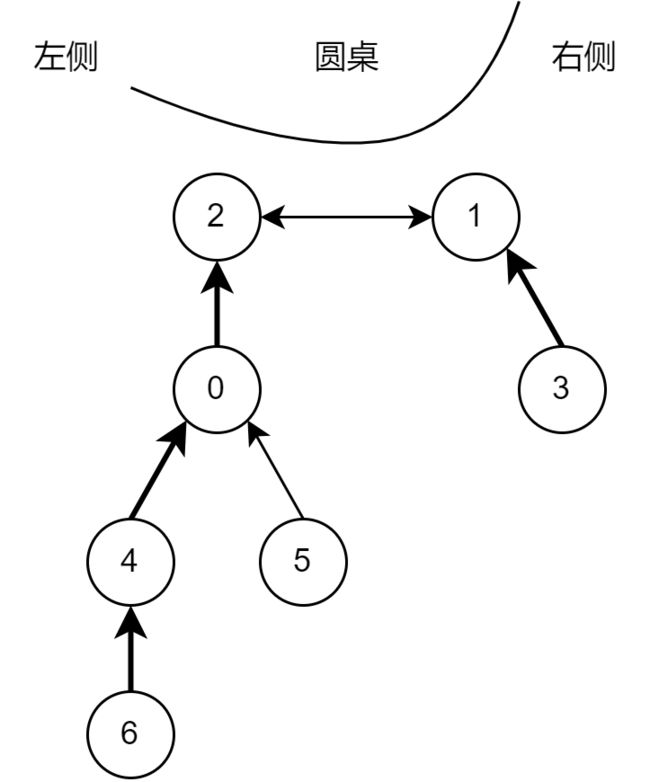
我们可以先让员工 2 和 1 坐在圆桌旁，员工 2 在左侧，员工 1 在右侧，那么 2 这一侧的树枝只能坐在 2 的左侧，而 1 这一侧的树枝只能坐在 1 的右侧。0 可以紧靠着 2 的左侧坐下，4 和 5 只能有一个人坐在 0 的左侧。为了在圆桌旁坐下尽可能多的人，我们需要从 2 出发，沿着反图方向的边找，每个点在其反图上只能选择一个子节点，最后找到一条最长的链，即图中加粗的节点。

对于 1 一侧同理。将这两条最长链的长度之和即为该基环树能组成的圆桌的最大员工数。

对于多个基环长度等于 2 的基环树，每个基环树所对应的链，都可以拼在其余链的末尾，因此可以将这些链全部拼成一个圆桌，其大小记作 sumChainSize。

最终返回的答案即为 max⁡(maxRingSize,sumChainSize)。

功能实现

解题思路已经理清楚了，现在要来看看需要实现哪些功能（做什么）：

• 建立反图；
• 根据反图求图中树枝上的最大链；
• 求图中所有基环的长度，按照基环的长度来分类讨论参加会议的最多员工数量。

建立反图

先统计所有节点的入度，然后从入度为 0 的节点开始，建立反图。

求最大链
根据反图求图中树枝上的最大链，就是求二叉树的最大深度的题目，使用递归实现，代码为：

int maxDepth(int x) {
    int maxDepth = 1;
    for (int son : rg[x]) {
        maxDepth = max(maxDepth, maxDepth(son) + 1);
    }
    return maxDepth;
}

基环的长度

我们枚举所有的节点，因为我们已经在拓扑排序的时候将树枝节点的入度全部置为 0 了，所以在枚举中遇到入度为 1 的节点，那么该节点一定是基环的入环点。

实现代码

class Solution {
public:
    int maximumInvitations(vector<int>& favorite) {
        int n = favorite.size();
        vector<int> deg(n);
        // 统计基环树每个节点的入度
        for (int f : favorite) {
            ++deg[f];
        }

        queue<int> que;
        for (int i = 0; i < n; ++i) {
            if (deg[i] == 0) {
                que.push(i);
            }
        }

        // 拓扑排序建反图
        vector<vector<int>> rg(n);
        while (!que.empty()) {
            int x = que.front();
            que.pop();
            int y = favorite[x];
            rg[y].push_back(x);
            if (--deg[y] == 0) {
                que.push(y);
            }
        }

        // 根据反图求图中树枝上的最大链
        function<int(int)> rdfs = [&](int x) -> int {
            int maxDepth = 1;
            for (int son : rg[x]) {
                maxDepth = max(maxDepth, rdfs(son) + 1);
            }
            return maxDepth;
        };

        int maxRingSize = 0, sumChainSize = 0;

        // 枚举所有节点，找到入环点计算基环长度
        for (int i = 0; i < n; ++i) {
            if (deg[i] == 0) continue;  

            deg[i] = 0;     // 将基环上的点的入度标记为 0，避免重复访问
            int ringSize = 1;
            for (int x = favorite[i]; x != i; x = favorite[x]) {
                deg[x] = 0; // 将基环上的点的入度标记为 0，避免重复访问
                ++ringSize;
            }

            if (ringSize == 2) {
                sumChainSize += rdfs(i) + rdfs(favorite[i]);// 累加两条最长链的长度
            }
            else {
                maxRingSize = max(maxRingSize, ringSize);   // 取所有基环长度的最大值
            }
        }
        return max(maxRingSize, sumChainSize);
    }
};

复杂度分析

时间复杂度：$\mathcal{O}(n)$。其中 $n$ 为 favorite 的长度。拓扑排序和遍历基环均为 $\mathcal{O}(n)$。

空间复杂度：$\mathcal{O}(n)$。

---

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 哦。