动态规划之打家劫舍(House Robber)-C语言实现
动态规划之打家劫舍(House Robber)-C语言实现
- 前言
打家劫舍是0-1背包经典问题的其中一类,其特征符合经典的动态规划求解流程,通过本经典习题的学习和理解,深入理解0-1经典问题背后的逻辑以及递归过程中二叉树的形成过程,很多情况下,动态规划的递归的结果最终形成二叉树(0-1问题,也即选择或舍弃)或多叉树(多个选择,选择类型分为离散和连续两类)。动态规划的核心思想是寻找正确的状态转移方程,能够从一类状态计算到另一类状态,最终达到求解的目的。
- 问题描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
198. 打家劫舍 - 力扣(Leetcode)
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
- 问题解决方案
遵从《算法导论》的CRCC原则,对本问题进行逐步解析,依照教材提供的步骤,开启动态规划的烧脑解题流程。首先需要表征最优问题的子结构,也就是说必须识别问题的最优子结构 (optimal substructure),最优子结构是动态规划的关键要素之一。
a) 表征最优问题的结构和递归定义最优问题的值-(CR)
| 房屋编号# | #0 | #1 | #2 | #3 |
|---|---|---|---|---|
| 屋内价值(?) | ? | ? | ? | ? |
假定小偷从#3到#1次序行窃,那么对于么个房子小偷都有两个选择,行窃或放弃;由于小偷是惯犯,偷盗手法非常专业,而且小偷也理解动态规划的决策思想,那么小偷就会根据每家每户的位置,以及户外装修判断屋内可盗窃价值,经过一些列的外部的明察暗访,小偷终于弄清楚屋内的盗窃价值。值得一提的是,小偷由于在户外活动,不闯入住宅,所以不会触动屋内报警装置。–专业!
| 房屋编号# | #0 | #1 | #2 | #3 |
|---|---|---|---|---|
| 屋内价值 | 2 | 7 | 9 | 3 |
接下来小偷需要解决的问题是,选择从哪边开始行窃,有个困惑一直荡在小偷的心头,到底从#0还是#3房屋开启偷盗活动呢?小偷身边恰有一位同谋惯偷,其同谋眨眨眼说道,#0号房屋距离US49公路更近,方便行窃后撤离现场,建议从#3号开始偷窃,一路向西至#0号完成;小偷则持有不同的意见,觉得#3号房子距离销赃地点更方便。此刻两人意见不同,僵持不下,最后小偷还是听从了“老偷”的意见,决定从#3号着手,方便逃离。
接下来,大家可能心生疑惑,从不同的方向选择行窃是否对最优结果有影响?答案是否定的,无论从那个方向开始,只要连续进行,最后得到的最优结果一定相同,后续将用C语言程序验证这个结果。
制定了偷窃起始点,接下来两个小偷就需要决定最终闯入哪个房子进行行窃,由于小偷虽然听过动态规划可以帮助满足其偷窃价值的最大化,但是小偷手头没有电脑,也不会编程,接下来怎么办呢?小偷拿出一张A4纸,开始对每户是否偷窃进行选择,两个小偷时刻谨记相邻的房屋装有相互连通的防盗系统,不能连续闯入用户进行行窃,当晚小偷也没有携带剪线钳,无法有效切断两户之间的防盗系统线路,只能接着月光手绘决策图。功夫不负有心人,三更刚过,盗窃指导图新鲜出炉。
看到眼前的盗窃图,小偷内心抑制不住激动,恨不得马上把钱财搞到手。等一等,我们逐层进行抽丝剥茧,挖掘信息。首先在最顶层,小偷想象着要进行偷窃,在进入#3号房屋之前,他们有两个选择,选择偷窃#3号房间,这个选择有得有失,得到的#3房屋内的财物,失去的是进入#2房屋行窃的机会,如果进入#2房屋,那么就会警铃大作,两个小偷只能束手就擒。
如果选择绕过#3房屋,接下来就来到了#2号房屋,对于#2房屋,此时小偷仍然有两个选择,偷窃#2号房屋或者绕开#2号房屋,放弃偷窃;
如果刚才在第一步选择行窃#3号房屋,那么接下来就只能绕过#2房屋,防窃偷盗,来到#1号房屋,对于#1号房屋小偷有选择行窃和防窃两个机会。
经过反复度量权衡,小偷罗列8个行窃方案,方案①的结果是善心大发,防窃所有房屋的行窃,当然最终也是一无所获。
对上述8个方案的赃物价值进行统计:
| Plan | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 7 | 9 | 11 | 3 | 5 | 10 |
小偷经过权衡,邪念还是冲昏了头脑,他们决定采用方案⑤进行行窃,获取最大偷窃价值。
接着分析小偷如实现最大偷窃价值的,小偷走到编号第#i的房子,面前有两个选择,行窃或绕过放弃,这时候需要对两类选择的综合价值进行判断,取最大的值。
f ( i , n u m s [ ] ) = m a x { f ( i − 1 , n u m s [ ] ) + 0 , f ( i − 2 , n u m s [ ] ) + n u m s [ i ] } ; f(i,nums[\ ])=max\{f(i-1,nums[\ ])+0,f(i-2,nums[\ ])+nums[i]\}; f(i,nums[ ])=max{f(i−1,nums[ ])+0,f(i−2,nums[ ])+nums[i]};
如果放弃第#i房屋的盗窃,那么盗窃的总价值就是第(i-1)号房屋之前盗窃总值的最大值,对于这个选择,带来的价值收益为0,原因是没有进入屋内偷窃,没有得到任何赃物;如果选择盗窃第#i房屋,那么就带来第#i房屋赃物价值收益nums[i], 同时必须放弃第#i房屋的盗窃,总价值等于第(i-2)号之前盗窃价值总值的最大值与当前选择的收益之和nums[i]。
b.) 计算最优问题的值(Compute the value of the optimal problem)
计算最有问题的值之前,一起回归一下动态规划的两大特征,最优子问题和重叠子问题,
- 最优子问题
首先确认是否存在最优子问题,如果需要求解f(i,nums[])那么就涉及到求解f(i-1, nums[ ])和f(i-2, nums[ ])两个最优子问题,最优子问题和原问题具有相同的结构特征,可以用同一思路求解。
- 重叠子问题
本题的重叠子问题不容易辨识,原因是子问题后面追加了不同的常量,经过分析,数组常量的选择对子问题本身没有任何影响,只要递归函数的参数值相同,无论后面选择带来的常量如何变化,我们都认为两个问题为重叠子问题。二叉树中的紫色矩形框内的子问题重叠,椭圆形(请忽略椭圆大小)绿框内的子问题也有重叠的特征。本题具有重叠子问题的显著特征。
- DAG 有向无环图
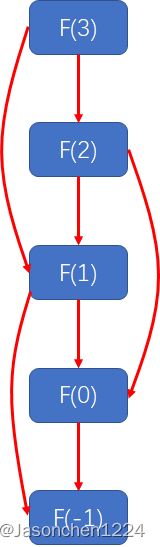
在这里补充一点,动态规划的子问题都具有相互独立性,子问题之间的依赖形成有向无环图(DAG),无环是子问题求解的关键,否则子问题互相依赖就导致递归或迭代没有结束条件或基础解。本体的DAG图可以简略表示为,每个问题依赖两个子问题,DAG图生动展现了迭代自低到顶的求解过程。备注:F(-1)=0。
递归+记忆方式的动态规划求解,回顾之前提到的问题,连个小偷就从哪边开始行窃意见不同意,那么我们就利用程序进行说明。
程序1:从#3房开始行窃,我们得到盗窃最高金额为11,
程序2: 从#0开始,同样得到盗窃最高金额为11,所以两位同事不要争吵,如果你们完成所有的房子的行窃,最高金额是没有差异的。
程序1:
/**
* @file rob_house.c
* @author your name ([email protected])
* @brief
* @version 0.1
* @date 2023-03-08
*
* @copyright Copyright (c) 2023
*
*/
#ifndef ROB_HOUSE_C
#define ROB_HOUSE_C
#include "rob_house.h"
int rob_house(int *nums, int *dp, int nums_size)
{
int i;
for(i=0;i<=nums_size;i++)
{
*(dp+i)=-1;
}
return rob_house_aux(nums,dp,nums_size);
}
int rob_house_aux(int *nums, int *dp, int nums_size)
{
int incl_current;
int excl_current;
int max_value;
if(nums_size<0)
{
return 0;
}
if(dp[nums_size]!=-1)
{
return dp[nums_size];
}
// not choose the current house,no value added
excl_current=rob_house_aux(nums,dp,nums_size-1)+0;
// choose current house, value added by nums[num_size]
incl_current=rob_house_aux(nums,dp,nums_size-2)+nums[nums_size];
max_value=max(excl_current,incl_current);
dp[nums_size]=max_value;
return dp[nums_size]; // int nums[] = {2, 7, 9, 3};
}
int max(int m, int n)
{
return (m>n?m:n);
}
#endif
程序2:
/**
* @file rob_house.c
* @author your name ([email protected])
* @brief
* @version 0.1
* @date 2023-03-08
*
* @copyright Copyright (c) 2023
*
*/
#ifndef ROB_HOUSE_C
#define ROB_HOUSE_C
#include "rob_house.h"
int rob_house(int *nums, int *dp, int start, int nums_size)
{
int i;
for(i=0;i<=nums_size;i++)
{
*(dp+i)=-1;
}
return rob_house_aux(nums,dp,start,nums_size);
}
int rob_house_aux(int *nums, int *dp, int start, int nums_size)
{
int incl_current;
int excl_current;
int max_value;
if(start>nums_size)
{
return 0;
}
if(dp[start]!=-1)
{
return dp[start];
}
// not choose the current house,no value added
excl_current=rob_house_aux(nums,dp,start+1,nums_size)+0;
// choose current house, value added by nums[num_size]
incl_current=rob_house_aux(nums,dp,start+2,nums_size)+nums[start];
max_value=max(excl_current,incl_current);
dp[start]=max_value;
return dp[start];
}
int max(int m, int n)
{
return (m>n?m:n);
}
#endif
测试程序
/**
* @file rob_house_main.c
* @author your name ([email protected])
* @brief
* @version 0.1
* @date 2023-03-08
*
* @copyright Copyright (c) 2023
*
*/
#ifndef ROB_HOUSE_MAIN_C
#define ROB_HOUSE_MAIN_C
#include "rob_house.c"
int main(void)
{
int nums[] = {2, 7, 9, 3};
int nums_size=4;
int max_value;
int start;
int dp[nums_size];
start=0;
max_value=rob_house(nums,dp,start,nums_size-1);
printf("The maximum value is %d\n",max_value);
getchar();
return EXIT_SUCCESS;
}
#endif
但如果深入思考,发现二者还是存在差异,差异点在于,如果行窃过程中被保安发现,没有完成所有房子的选择和放弃,这时候选择次序的差异就体现出来了,根据二者的动态数组dp值。
对于屋内物品价值:
| 房屋编号# | #0 | #1 | #2 | #3 |
|---|---|---|---|---|
| 屋内价值 | 2 | 7 | 9 | 3 |
如果从#0开始行窃,那么其dp值为
| 房屋编号# | #0 | #1 | #2 | #3 |
|---|---|---|---|---|
| 屋内价值 | 2 | 7 | 9 | 3 |
| DP(从#0至#3顺序) | 2 | 7 | 11 | 11 |
| DP(从#3至#0顺序) | 11 | 10 | 9 | 3 |
从效率上考虑,按照#0至#3,偷窃完成#2房屋后,就可以收手;反之如果从#3至#0,需要完成最后一个房屋#0盗窃后,才能获得最高金额。
如果考虑行窃途中被保安发现,放弃后续偷窃,那么#3至#0顺序则优选#0至#3的顺序,因为3>2以及9>7。
最后我们快速回顾一下bottom-up的代码实现方式,在此不再进行赘述。
/**
* @file rob_house.c
* @author your name ([email protected])
* @brief Use Bottom up to solve this problem
* @version 0.1
* @date 2023-03-08
*
* @copyright Copyright (c) 2023
*
*/
#ifndef ROB_HOUSE_C
#define ROB_HOUSE_C
#include "rob_house.h"
int rob_house(int *nums, int *dp, int nums_size)
{
int i;
dp[0]=nums[0];
dp[1]=max(nums[0],nums[1]);
for(i=2;i<nums_size;i++)
{
dp[i]=max(dp[i-1]+0,dp[i-2]+nums[i]);
}
return dp[nums_size-1];
}
int max(int m, int n)
{
return (m>n?m:n);
}
#endif
- 总结
通过本题学习,对0-1 选择递归和迭代有了更深入的认识,在脑海中可以形成一副环环相扣的迭代图,同时也逐步体会到0-1选择可以形成二叉树,多种选择就形成多叉树,总之最后遍历的结果都是形成树;对于迭代的基础DAG图像,实际上它是二叉树或多叉树相同节点互相压缩后形成的结果,其主要特点是有向无环。
参考资料:
- 198. 打家劫舍 - 力扣(Leetcode)
- 《Introduction to algorithm, 4ed》