基于胡桃夹子优化算法 (NOA)求解单目标优化问题附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

⛄ 内容介绍

胡桃夹子优化算法 (NOA) 是一种受自然启发的算法，可模拟胡桃夹子鸟在两个不同时期的不同行为。NOA 针对二十九个测试函数、CEC-2014、CEC-2017 和 CEC-2020 以及五个实际工程设计问题进行了评估。将 NOA 与三类现有优化算法进行比较：(1) SMA、GBO、EO、RUN、AVOA、RFO 和 GTO 作为最近发布的算法，(2) SSA、WOA 和 GWO 作为高引用算法，以及(3) AL-SHADE、L-SHADE、LSHADE-cnEpSin 和 LSHADE-SPACMA 作为高性能优化器和 CEC 竞赛的获胜者。与 LSHADE-cnEpSin 和 LSHADE-SPACMA 作为性能最佳的优化器和 CEC-2017 的获胜者相比，NOA 在所有方法中排名第一并表现出优异的结果，

⛄ 部分代码

%_________________________________________________________________________%

%  Nutcracker Optimization Algorithm (NOA) source codes demo 1.0               %

%                                                                         %

%  Developed in MATLAB R2019A                                      %

%                                                                         %

%  Author and programmer: Reda Mohamed (E-mail: [email protected]) & Mohamed Abdel-Basset (E-mail: [email protected])                              %

%                                                                         %

%   Main paper: Abdel-Basset, M., Mohamed, R.                                    %

%               Nutcracker optimizer,                         %

%               Knowledge-Based Systems, in press,              %

%               DOI: https://doi.org/10.1016/j.knosys.2022.110248   %

%                                                                         %

%_________________________________________________________________________%

clear all

clc

SearchAgents_no=25; % Number of search agents

Max_iteration=400; % Maximum number of Function evaluations

RUN_NO=2; %% Number of independent runs

for i=1:23 %% Test functions

  for j=1:RUN_NO

   [lb,ub,dim,fobj]=Get_Functions_details(i);

   [Best_score,Best_pos,Convergence_curve]=NOA(SearchAgents_no,Max_iteration,ub,lb,dim,fobj);

   fitness(1,j)=Best_score;

  end

  fprintf(['Function_ID\t',num2str(i),'\tAverage Fitness:',num2str(mean(fitness(1,:)),20),'\n']);

  %% Drawing Convergence Curve %%

  figure(i)

  subplot(1,2,1);

func_plot(strcat('F',num2str(i)));

title('Parameter space')

xlabel('x_1');

ylabel('x_2');

zlabel([strcat('F',num2str(i)),'( x_1 , x_2 )'])

subplot(1,2,2);

  h=semilogy(Convergence_curve,'LineWidth',2,'Color','r');

%   h.MarkerIndices = 1000:1000:Max_iteration;

  xlabel('Iteration');

  ylabel('Best Fitness obtained so-far');

  axis tight

  grid off

  box on

  legend({'NOA'});

end

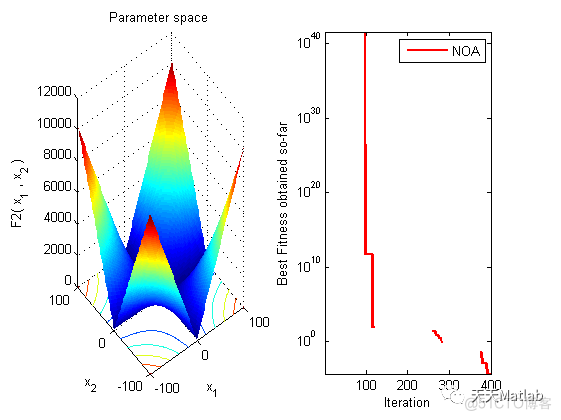
⛄ 运行结果

⛄ 参考文献

Main paper: Abdel-Basset, M., Mohamed, R., Jameel, M., & Abouhawwash, M. (2023). Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowledge-Based Systems, 110248, DOI: https://doi.org/10.1016/j.knosys.2022.110248

⛳️ 完整代码

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料