词法分析:从RE(正则表达式)到DFA(确定的有限状态机)
模式识别(Pattern recognization)是现在非常流行的一个词,我们对词法的分析也是基于模式(pattern-based)的。我们用正则表达式(Regular Expression)来定义单词的模式,而在词法分析时,有限状态机(Finite Automata)更便于我们分析。本文介绍将正则表达式(RE)转为确定的有限状态机(DFA)的方法。
首先,什么是确定的有限状态机,什么是非确定的有限状态机(NFA)?用通俗的语言讲,在面对相同的输入参数时,NFA可能会跳转到多种状态,而DFA只会跳转到特定的状态,有DFA类似于函数,而NFA类似一对多的映射。
DFA用程序可以描述为:
state = 1;
while (true) {
ch = getChar();
switch(state) {
case 1:
if (ch == 'a')
state = 1;
else if (ch == 'b')
state = 2;
else error();
break;
case 2://终止状态
if (ch == 'a') state = 2;
if (ch == '1') state =2;
else {
ungetChar();//把取出的字符放回去
return ID;
}
}
}从上面的代码段,我们需要知道:
- DFA=>program:从确定的有限状态机可以生成确定的程序
- Each state=>a fragment of code:每个状态对应一个case。
- Each edge=>a judgement:每条边对应一个if判断
从RE推出DFA的步骤:RE=>NFA=>DFA=optimization=>DFAo=>program
1. 从RE到NFA
从正则表达式到非确定的有限状态机对于人来说非常好理解,但是对于机器来说确比较复杂。从RE到DFA有两种方法:自顶向下逐步分解法和自下而上组合方法(Thompson方法)。
自顶向下逐步分解法:Top-down stepwise refinement according to the structure of RE
这种方法符合人的思维习惯,首先我们从最简单的情况开始考虑。
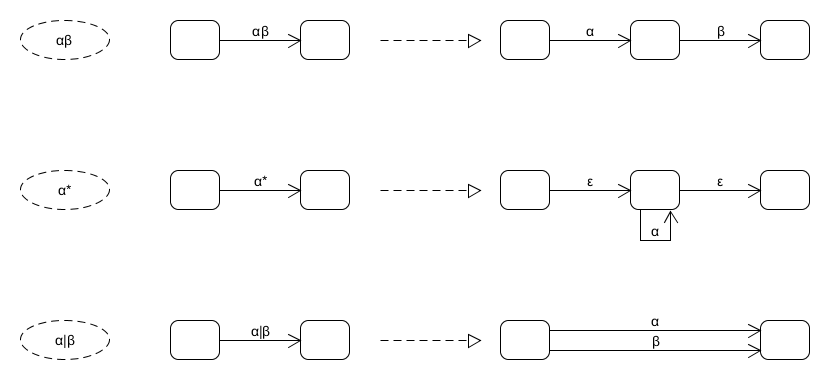
以(a|b)* a (a|b) (a|b)为例,这个正则表达式符合上面的αβ特征,因此第一步可以变成:

而对于(a|b)*,又符合上面的a*特征,因此(a|b)*可以继续分解为
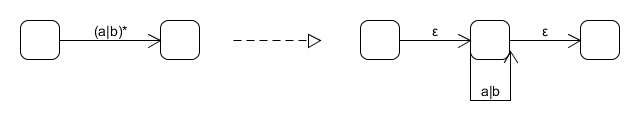
可以看到a|b还可以继续分解,类似这样的分解过程到所有边的标记只剩下ε或字母表的单一字符为止。
然而,对于计算机来说,字符是一个一个读入的,计算机不能从整体把握情况逐步向下分解,因此我们还需要适合计算机的方法。
自下而上组合法:Bottom-up combination(Thomson方法)
这种比前一种方法稍微复杂一点,但其实想法也很简单,我试着换一种表述来解释这个方法。
在遇到单个的字符时,我们直接构造转换图,比如遇到a时,我们就构造这样的转换图:
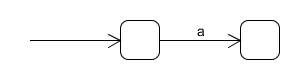
这样,我们就形成了一个单元U,这个U就是上面已经生成的转换图。
在遇到操作符时,我们所有的处理都是针对单元的,在下面的图示中,我们用虚线圆圈表示一个单元。
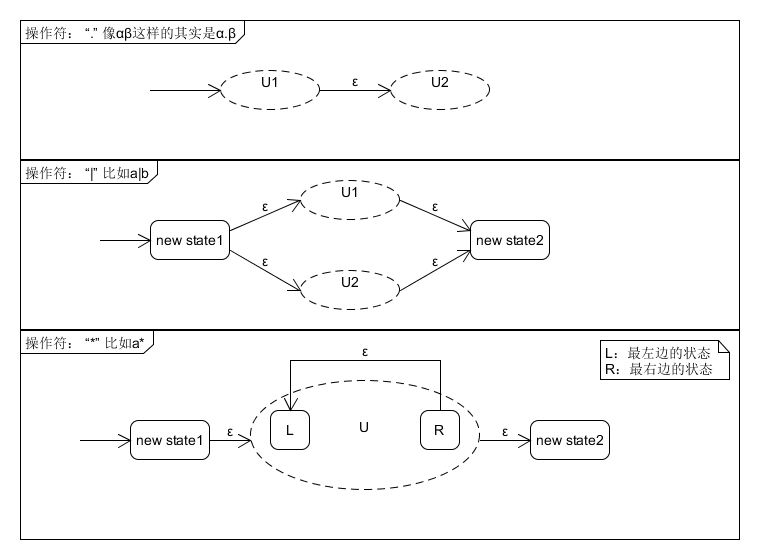
在处理完操作符后形成的仍是一个单元,处理完后的整体变成单元U’参与下一次处理。这里类似于一种递归的过程。
但是,像a|b这样的式子,在处理‘|’这个操作符时,我们显然需要两个单元,但计算机在读到‘|’操作符时,我们在为a构造了转换图,计算机还不知道b的存在,也就不能做上面这样的处理,所以这种方法需要以下条件:
- 正则表达式(RE)需要处理为后缀表达式
- 正则表达式(RE)中需要写明操作符‘.’,如ab需要写为a.b
满足以上条件后,计算机可以用这种方法自动生成NFA。
2. 从NFA到DFA
对于一个已经形成的NFA,我们需要定义新的状态来形成DFA。首先要解释两种方法和他们对应的使用情形。
NFA之所以为NFA而不是DFA,主要是因为以下两个原因,解决以下的两种情形,就能将NFA转为DFA。
边上的ε:ε闭包
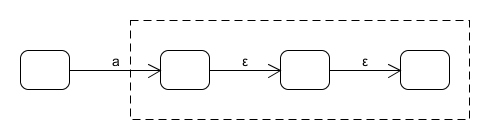
遇到这种情况,后面的三个状态完全可以合并,如果将后面的三个状态合为一个,那这个转换图里就没有ε边,也就满足了DFA的条件。
对应的解决方法是找出ε闭包,也就是先找出该状态的ε边推出的所有状态,再找那些状态的ε边推出的状态,是一个迭代的过程,直到找出一个状态的ε闭包。如果是从状态x开始的,我们将通过该过程找到的所有状态集称为以x状态为核的ε闭包,记为ε-closure({x}),或ε-c({x})。从定义可以知道,核相同,推出的ε闭包一定相同。
不确定的后续状态:子集构造法
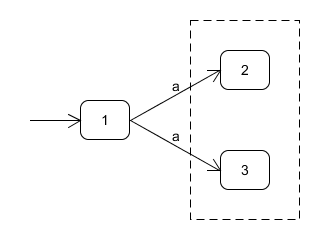
遇到这种情况,如果能将状态2和状态3合并到一起,就不会出现“面对相同的输入状态可能跳转到多种状态的情形了”,合并状态2和状态3这样类似的状态的方法叫做子集构造法,若从状态Ii开始,以a边推出的所有状态集合为B,我们记为Ii–a–>B,比如上图可以记为1-a->{2,3}
综合使用:表驱动法
上面只是简单介绍了两种情形,说明了从NFA转化到DFA的重点是重新组合NFA状态。下面我们讨论系统的可编程的过程来将NFA转化为DFA,运用的还是上面的两种方法,我们需要构建一张表来展示构建的DFA里的所有状态。
以下图中的NFA为例:
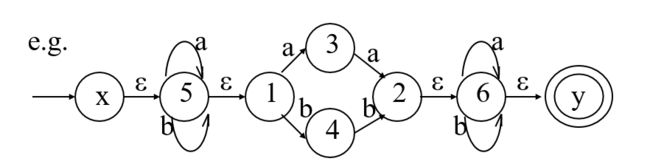
| DFA State Ii (这里是新生成的DFA里的状态) | a(这个状态从a边推出什么状态) | b (这个状态从b边推出什么状态) |
|---|---|---|
| I0=ε-c({x})={x,5,1} | ε-c(I0-a->{5,3})={5,3,1}=I1 | ε-c(I1-b->{5,4})={5,4,1}=I2 |
| I1={5,3,1} | … | … |
| I2={5,4,1} | … | … |
解释:首先从起点x开始构造新的DFA里的第一个状态I0,也就是寻找以x为核的ε闭包ε-c({x}),然后构造新的I0从a、b边推出的状态,方法是先使用子集构造法,再寻找构造后的子集的ε闭包。这样我们就找到了新的状态I1,I2,第二行、第三行就是寻找I1,I2以a、b边推出的状态,这样就能找到更多的状态,当没有新的状态产生时,这样的过程终止。这类似于一种迭代的过程。
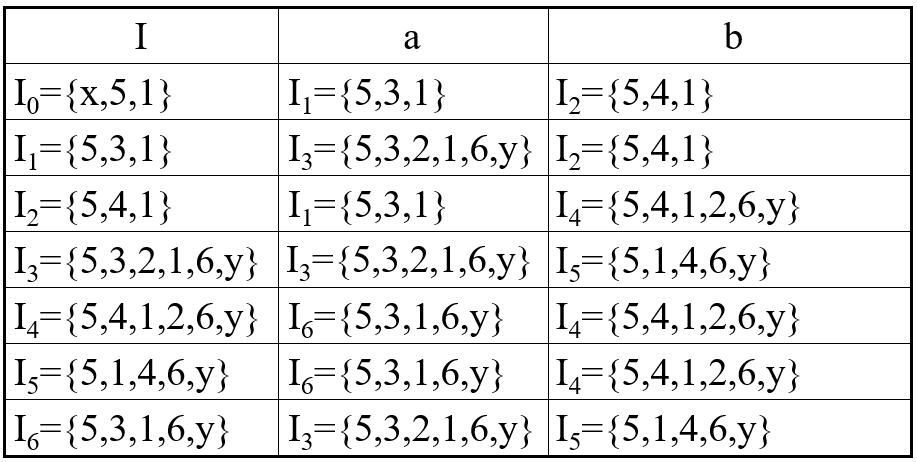
这题最终的结果是:
3. 从DFA到DFAo(DFA优化)
在上面生成的DFA中,每个状态都有以a、b推出的状态,有时候这可能意味着多余。DFA优化(Optimization of a DFA)的思想是减少DFA中的状态,我们用到离散数学中等价类划分的思想,如果两个状态等价,那么他们属于同一个等价类,我们只需要选择其中的一个代表即可。
如何划分等价类呢?
1)找出终止状态
什么样的状态可以被称为终止状态呢?在上例的NFA图中,y状态为终止状态。我们要做的是在I0~I6中找出终止状态。我们这样定义新的DFA中的终止状态:若Ii ∩ y ≠∅ ,则Ii为DFA中的终止状态。
因此第一步我们将上面的状态分为两类:终止状态和非终止状态。

2)划分等价类
第一步已经将状态分为了两类,下面我们要继续拆分。我们规定这样的这样的状态Ii,Ij属于同一个等价类:
- Ii,Ij发出的边数相同。
- Ii,Ij发出的边相同。
- 对应相同的边连接的状态属于同一个等价类。
如I0和I1,他们对应的a边发出的状态分别是I1和I3,而在第一步中这两个状态已经被划分到了两类里,一定不是等价的,所以我们将I0,I1拆分,也就是将I0单独分出去。

3)回头看
在划分完后面的等价类时,我们还要回头看一下前面的等价类还可不可以划分。有时候前面在比较时后面的类还没有划分,因此判断属于同一个等价类不拆分,而到后面等价类判断时拆分了这个等价类,前面判断的两个状态可以就到了不同的等价类里,这就需要我们回头检查是不是所有的类都不能再拆分了。
4)选取代表
分好等价类后每个类选取一个状态作为代表,这个类的其他状态都用这个代表代替,重新构造DFA转化图。
这样,我们就将RE转换成优化后的DFA,尽管过程比较复杂,但是这样机械而固定的过程是可以编程解决的。在构造完DFA后,我们可以开始做更多的词法分析工作。