Nuist集训队作业：深度优先搜索（回溯算法）

引例

国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法？
（在国际象棋中皇后的移动范围是它所在的一整行一整列以及两条对角线，呈米字型）
我们把问题延展开来，把n（n>=4）个皇后放在n*n的棋盘上有几种摆法？
先尝试解决四皇后问题：
由于棋子不能占同一行，所以不妨把的n个棋子摆在第n行，来考虑它是否合适。
1.先对第一个棋子进行枚举，假设它放在（1,1）位置。
2.然后摆放第二个棋子，由之前操作可知，（2,1），（2,2）无法摆放。不妨把第二个棋子放在（2,3）的位置。
3.现在摆放第三枚棋子，由之前两次操作，（3,1），（3,2），（3,3），（3,4）都已无法摆放，所以第二个棋子摆放不恰当，返回步骤2，我们要对第二个棋子重新摆放。
4.把第二个棋子放在（2,4），此时第三行（3,2）位置正好空着，把第三个棋子摆上去。
5.最后摆第四个棋子，由于之前的摆放情况，该行已被完全占领，这就说明之前的摆放存在错误。追根溯源，我们只能对第一个棋子的位置重新枚举，把它放在（1,2），再对剩下三枚棋子也依次重新操作。
…
经过多次枚举，得到四皇后的解如下：

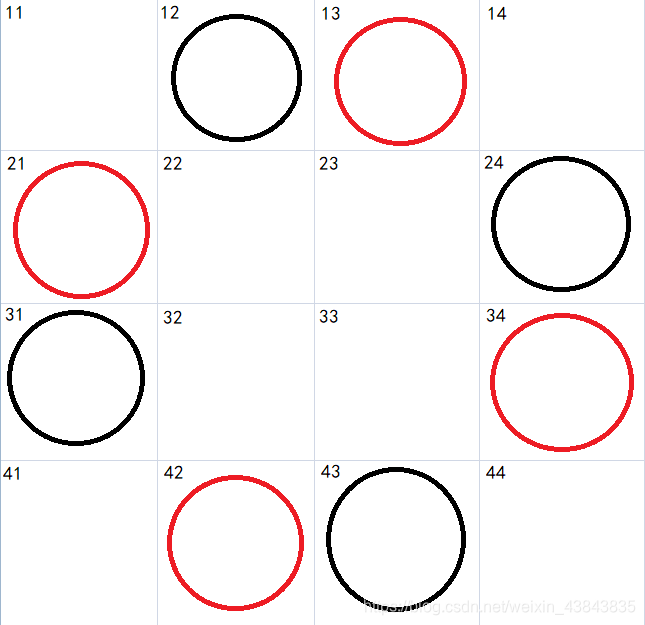
当四个棋子分别位于（1,2），（2,4），（3,1），（4,3）或分别位于（1,3）、（2,1）、（3,4）、（4,2）时它门是互不冲突的。由此我们得出n=4时的解为2。
那么当n=8时，我们是否也可以用类似的方法枚举得出呢？
设计一个程序输出某个数的全排列，是否也是这样的思想呢？

深搜基本思想及回溯算法模板

根据八皇后的列子，我们得出这类问题的基本思路。
每一次枚举，我们有两种判断结果：
1.满足，继续枚举下一层。如果是最后一层，则得出结果。
2.不满足，回到上一层，枚举同层的下一种情况。
伪代码模板：

void dfs(层数及其它参数)
{
	if(已经是最后一层，满足条件）
	{
		得出结果；
		返回；
	}
	else
	{
		for(枚举这一层的情况）
			if(满足题意）
			{
				标记该情况；
				dfs(层数+1及其它参数变化情况)；
				撤销标记(回溯);
			}
	}
}

P1706 全排列问题

题目链接(洛谷)
简单描述一下：
如果输入3，则输出：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
针对n=4这种情况，我们可以画出它的树，结构如下：

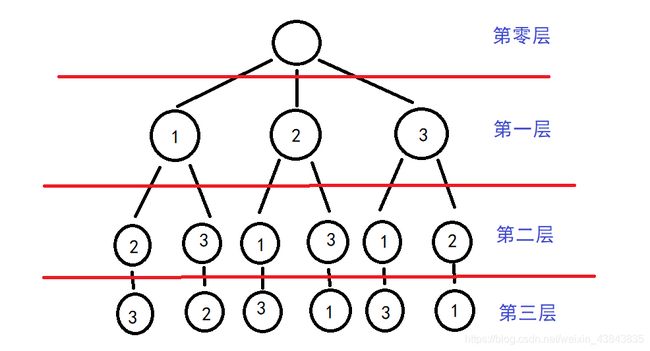
依据之前给出的伪代码模板，可以写出如下代码：

#include
int ans[10];//把取走的数字存入答案中 
int check[10];//用于标记该数字是否已经被取走 
int n;
void dfs(int dep)
{
	int i;
	if(dep==n+1)//所有数字都被取完，输出这一序列 
	{
		for(i=1;i<=n;i++)
			printf("%5d",ans[i]);
		printf("\n");
		return;
	}
	else
	{
		for(i=1;i<=n;i++)
			if(check[i]==0)//如果该数字在之前没有被取走 
			{
				ans[dep]=i;//将该数字存入答案序列中 
				check[i]=1;//标记该元素，表示已经取走 
				dfs(dep+1);//进入下一层查找尚未被取走的数或得出答案序列 
				check[i]=0;//回溯，撤除标记，枚举该层的下一种情况 
			}
	}
}
int main()
{
	scanf("%d",&n);
	dfs(1);
	return 0;
}

P1219 八皇后

题目链接(洛谷)
依据引例中的思想，尚有一个待解决的问题，如何用判断放下去的这枚棋子是否与前面i个棋子冲突。我们不必另外开一个棋盘来记录被标记的位置，这样过于浪费时间。我们可以开三个数组分别表示列、正对角线、副对角线。
设之前某一个棋子的坐标为(x,y)，即将放下的棋子的坐标为待定的(i,j)
列满足y!=j；
正对角线满足x+y!=i+j；
副对角线满足x-y+n!=i-j+n（加上n保证两边都大于0，便于数组存储标记）；
判断方法具体实现如下：

/*待放入棋子坐标为(i,j)*/
int c[26];//标记列 
int d1[26]; //标记正对角线 
int d2[26];//标记副对角线 
if(c[j]==0&&d1[i+j]==0&&d2[i-j+N]==0)
			{
				ans[i]=j;
				c[j]=1;
				d1[i+j]=1;
				d2[i-j+N]=1;
				dfs(i+1);
				c[j]=0;
				d1[i+j]=0;
				d2[i-j+N]=0;				
			}

全部代码：

#include
int N
int ans[26];
int c[26];//标记列 
int d1[26]; //标记正对角线 
int d2[26];//标记副对角线 
int ct;
void dfs(int i)
{
	int j,k;
	if(i==N+1)
	{
		ct++;//记录解的数量 
		if(ct<=3)//判断是否已经输出三组解 
		{
			for(k=1;k<=N;k++)
				printf("%d ",ans[k]);
			printf("\n");
		}
		return;
	}
	else
	{
		for(j=1;j<=N;j++)
			if(c[j]==0&&d1[i+j]==0&&d2[i-j+N]==0)
			{
				ans[i]=j;
				c[j]=1;
				d1[i+j]=1;
				d2[i-j+N]=1;
				dfs(i+1);
				c[j]=0;
				d1[i+j]=0;
				d2[i-j+N]=0;				
			}
	}
}
int main()
{
	scanf("%d",&N);
	dfs(1);
	printf("%d\n",ct);
	return 0;
}

P1605 迷宫

题目链接(洛谷)
本题中的每一层即为在迷宫中走的每一步，而每一步又分出四个方向(这四个方向所通往的坐标不一定是子树，可能是前面已被标记过的方格)。
对于在四个方向的移动，可以开两个一维数组，用坐标的加减表示移动：

int dx[4]={1,0,-1,0};//x轴上的移动法则
int dy[4]={0,1,0,-1};//y轴上的移动法则
/*i=0,1,2,3时分别表示向下、右、上、左*/

或者也可以开一个二维数组：

int move[4][2]={{1,0,-1,0},{0,1,0,-1}};
/*用move[0][1]表示下移，以此类推*/

以下贴出代码：

#include
int N,M,T,ct,SX,SY,FX,FY;
int dungeon[10][10];//标记走过的路径 
int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};//表示移动的数组 
int tx[26],ty[26];//获取障碍的位置，并标记在dungeon数组中 
void dfs(int sx,int sy)
{
	int i;
	if(sx==FX&&sy==FY){ct++;return;}//到达终点，方案数+1 
	else
	{
		for(i=0;i<4;i++)
			if(sx+dx[i]>=1&&sx+dx[i]<=N&&sy+dy[i]>=1&&sy+dy[i]<=N&&dungeon[sx+dx[i]][sy+dy[i]]==0)//判断移动是否越界，以及是否被走过 
				{
					dungeon[sx+dx[i]][sy+dy[i]]=1;//朝dx[i],dy[i]方向走，并标记前往的方格 
					dfs(sx+dx[i],sy+dy[i]);//走下一格 
					dungeon[sx+dx[i]][sy+dy[i]]=0;//撤掉标记，重新选定方向 
				}	
	}
}
int main()
{
	int i;
	scanf("%d %d %d",&N,&M,&T);
	scanf("%d %d %d %d",&SX,&SY,&FX,&FY);
	for(i=1;i<=T;i++)
	{
		scanf("%d %d",&tx[i],&ty[i]);//读取障碍位置，并在地图上标记出来 
		dungeon[tx[i]][ty[i]]=1;
	}
	dfs(SX,SY);
	printf("%d\n",ct);
	return 0;
}

这样还是不能AC，
最重要的起点没有首先打上标记。
（因为这个WA到自闭QAQ）
我们需要在main()函数中合适位置添加:

dungeon[SX][SY]=1;

P1101 单词方阵

题目链接(洛谷)
本题的树长得有点清奇：

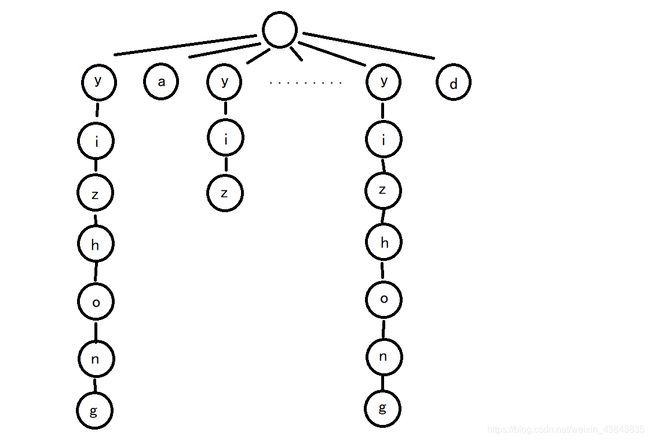
思路如下：
1.首先对地图进行逐个字符的查找，找到一个“y”。
2.我们对找到的“y”进行八个方位的查找，如果有“i”，顺着找到“i”的方向一路查找；如果没有“i”，撤销起点的标记。
3.顺着找到“i”的方向查找，如果能连续的一直查找到“g”，保存查找时留下标记；如果断链，不打标记，并且撤销起点的标记。
（需要注意的时，一个“y”附件八格可能不止一个“i”。如果所有的“i”都无法得出正确结果，才撤销“y”处标记）
八方移动数组:

/*移动法则参考P1605中的例子*/
int dx[8]={-1,0,1,1,1,0,-1,-1};//表示x方向上的移动 
int dy[8]={-1,-1,-1,0,1,1,1,0};//表示y方向上的移动

判断是否断链的代码：

char map[101][101];//原地图 
char check[8]={'y','i','z','h','o','n','g'};//顺着某方向移动是否有这些元素对应 
int ans[101][101];//用于做标记的地图 
int dx[8]={-1,0,1,1,1,0,-1,-1};//表示x方向上的移动 
int dy[8]={-1,-1,-1,0,1,1,1,0};//表示y方向上的移动 
int n;
void start(int x,int y)
{
	int i,j,flag,X,Y,Flag=0,ct;
	for(i=0;i<8;i++)
		if(x+dx[i]>=0&&x+dx[i]<n&&y+dy[i]>=0&&y+dy[i]<n&&map[x+dx[i]][y+dy[i]]==check[1])//如果dx[i],dy[i]方向上有"i" 
		{
			flag=1;//判断是否断链 
			ans[x][y]=1;
			for(j=1,ct=1;j<=6;j++,ct++)
			{
				X=x+j*dx[i],Y=y+j*dy[i];
				if(X>=n||Y>=n||X<0||Y<0||map[X][Y]!=check[ct])//判断是否越界，已经是否对应 
				{
					flag=0;
					break;
				}
			}
			if(flag==1)//如果没有断链，把这个方向上的6个元素打上标记 
			{
				Flag=1;//表明该方向上已经有解，即使其他"i"方向上断链，也不会撤销起点"y"标记 
				for(j=1;j<=6;j++)
				{
					X=x+j*dx[i],Y=y+j*dy[i];
					ans[X][Y]=1;
				}
			}
			ct=1;
		}
	if(Flag==0)
		ans[x][y]=0;
}

把这些没有断链的元素打上标记后，按照标记输出map中的元素，其余无标记元素则输出“*”。

int main()
{
	int i,j;
	scanf("%d",&n);
	for(i=0;i<n-1;i++)
		scanf("%s\n",map[i]);
	scanf("%s",map[i]);
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			if(map[i][j]=='y')
				start(i,j);
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			if(ans[i][j]==1)
				printf("%c",map[i][j]);//输出保留标记的字母，其余用"*"取代 
			else
				printf("*");
		}
		printf("\n");
	}
	return 0;
} 

小结

这四道题按照个人理解从易到难依次给出了解答。
解法也不一定就是完美的，还存在许多冗余的地方。
OK，作为第一次在CSDN上发表题解，就这样吧。
2018/11/29