宏观经济学 索洛模型

索洛增长模型，又称新古典经济增长模型、外生经济增长模型，是在新古典经济学框架内所提出的著名的经济增长模型。
主要用于解释固定资本增加，对GDP 所产生的影响。
该模型假设投资的边际收益率递减，即在一定数量后生产得越多，效率越低。
模型结论：经济增长的路径是稳定的。在长期只有技术进步是增长的来源。

第八章

前提

假设1：生产函数规模报酬不变，即：$zY=F(zK,zL)$
注意：规模报酬不变，不是边际收益不变

生产函数除以人数L，则得到：
$Y/L=F(K/L,1)$

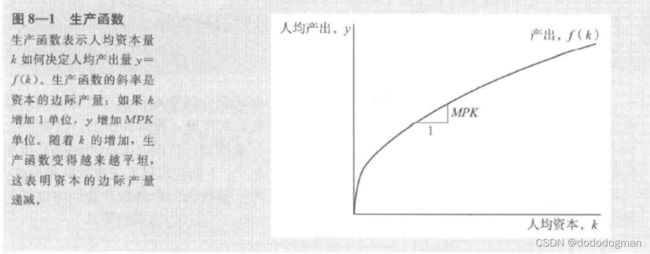
即，人均产出仅与人均资本（存量）相关

定义：
$y=Y/L$
$k=K/L$

生产函数表示为：$y=f(k)=F(K/L,1)$

平衡的增长，在达到稳态后持续稳定增长
水平的增长，是在达到稳态前的短暂增长，在达到稳态后维持水平不再增长

生产函数

名词解释：在一定时期内，在技术水平不变的情况下，生产中所用的各种生产要素的数量与所能生产的最大产量之间的关系

最常见的生产函数：柯布-道格拉斯生产函数（貌似不考）

$Y=F(K,\bar{L})=A{K}^{\alpha }{L}^{\beta }$

α+β＞1，则规模报酬递增；

α+β = 1，则规模报酬不变；

α+β＜1，则规模报酬递减。

Y代表GDP收入，A代表效率，K代表资本（资本存量），L代表生产人数；
$\alpha ,\beta$分别代表资本和劳动的产出份额（或产出弹性）

消费函数

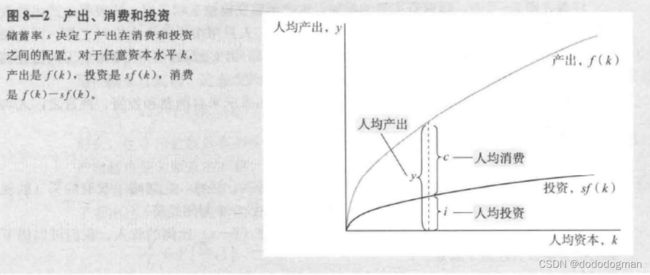
人均：$y=c+i$（先不考虑政府购买和进出口）
设储蓄率为 $s$
则用于消费得比例 $c=(1-s)y$ 带入上式
得：
$i=sy$
即，储蓄率即为用于投资得比例

资本存量 投资 折旧

投资：资本存量增长
折旧：资本存量减少

注意：$k$ 为资本存量，$i$ 为投资即为资本增长量

投资

对于消费函数推导结果：$i=sy$，将生产函数带入
得：
$i=sf(k)$
这个式子将存量和增长量联系在了一起，存量越大，增长量越大

折旧

折旧定义为资本存量k每年磨损的比例 $\delta$（定值）

资本存量的变动

显然：
$\Delta k=sf(k)-\delta k$

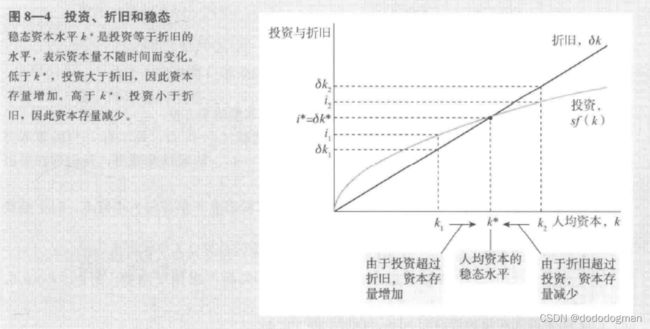
显然，$k^{\ast }$点资本存量稳定，定义为稳定状态

稳态代表经济的长期均衡

而当储蓄比例 s 变动时：

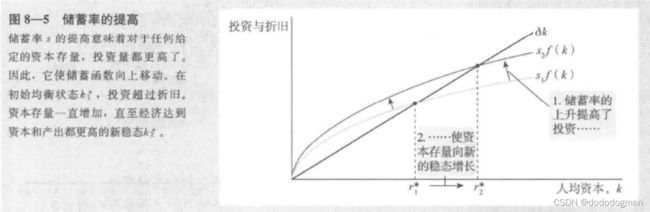
长期中，高的储蓄率代表更高的资本存量和国民收入
（持续性预算赤字的弊端：政府减少国民储蓄并挤出投资）
（预算赤字=财政赤字=财政支出>财政收入）

结论

注意：gdp是个流量，经济的增长是流量的增长，而不是存量，也就是Y保持在一个高水平不意味着经济增长，而是经济保持在高的产出水平。
真正的经济增长是指产出Y的持续增长

综上，索洛模型告诉我们：
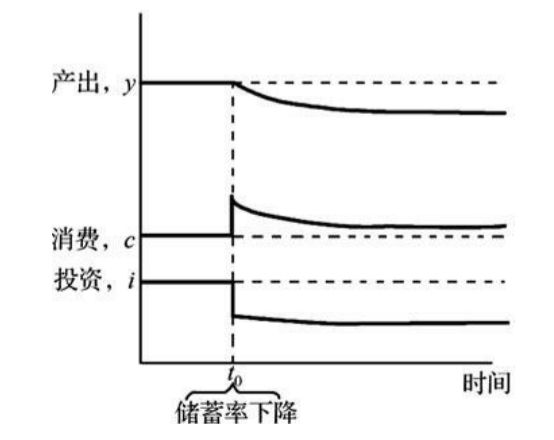
高的储蓄率会带来经济增长（y上升），但只是暂时的（达到新的稳定状态）；
储蓄率保持在高的水平，会保持高的资本存量 k 和生产水平 y，但不会永远保持高的经济增长率

黄金律水平

高的储蓄率虽然带来高的收入，但显然不是越高越好：当储蓄率为 1 时，有着最高的收入水平，但每个人都不花一分钱

作为一个仁慈的决策者，其目标是让每一个个体的福利最大化，因此，
最理想的储蓄率水平是使每个个体的消费水平最高的储蓄率
这个储蓄率被称为黄金律水平 $=k_{gold}^{\ast }$

$c=y-i$
在稳态水平下，投资等于折旧：$i=sf(k^{\ast })=\delta k^{\ast }$
将该式带入，收入y用函数表示，得：
$c^{\ast }=f(k^{\ast })-\delta k^{\ast }$

对$k^{\ast }$求导令其为0
$f(k^{\ast })$的导数即为MPK，因此求得$MPK=\delta$
此时人均消费最高，也是最理想福利最大化的情况

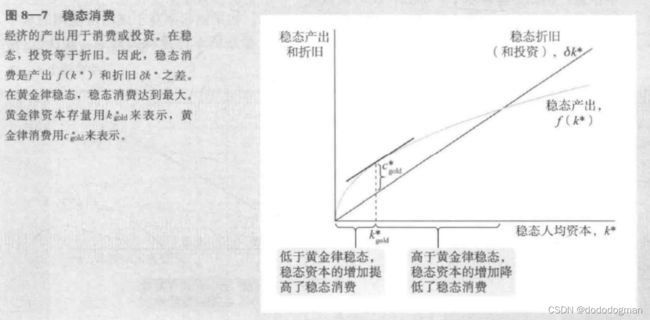
注意黄金律图中的曲线不是投资，而是产出，此时直线代表稳态的折旧，同时等于稳态投资
此时寻找产出和投资的最大差值

需注意，经济不会自发的走向$k_{gold}^{\ast }$，需要由决策者通过控制储蓄率来控制资本存量的水平

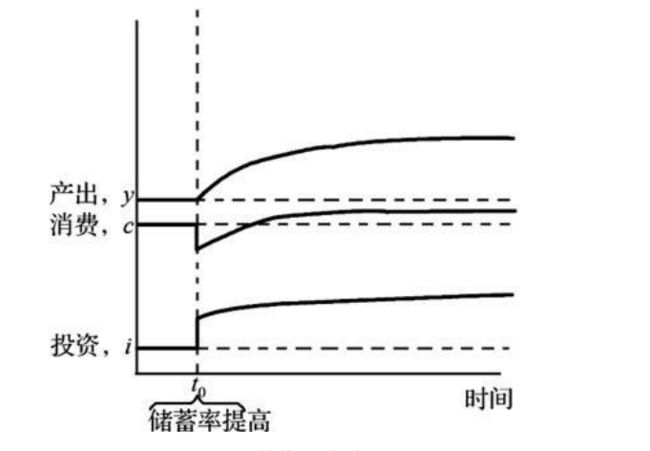
控制s的情况如下图，很容易理解

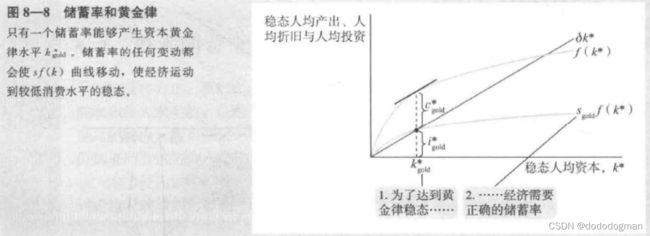
注意，达到黄金律水平时产出自然会变化，并且制定政策后会有一个稳定的过程，具体情况见下图

初始高于黄金律时：

低于：

带入人口增长的索洛模型

首先，先前的模型仅能解释经济的水平增长，并不能解释经济的稳态增长
当引入人口变量后，可以解释经济的总体增长，但并不能解释人均水平的增长

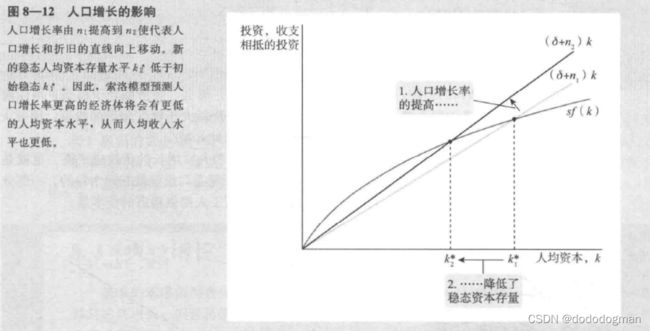
人口增长率：n
每年都会有新的劳动力产生，因此资本的增加量需要满足这部分新增的劳动力的需求
所以，新的平衡需要变动

因此在平衡时，每年增加的资本一部分用于抵消资本的折旧$\delta k$，一部分用于新增的劳动力对资本的需求$nk$:

$\Delta k=sf(k)-\delta k-nk$

平衡时：$i=(\delta +n)k$

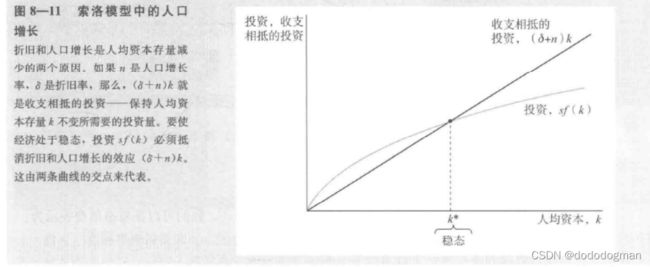
另外，当人口增长率变化时，平衡态也会变化：

这便是索洛模型对高人口增长率的国家更贫穷的预测

引入人口的黄金律水平

很简单，带入求解
$c^{\ast }=f(k^{\ast })-(\delta +n)k^{\ast }$
得：
$MPK=n+\delta$

第九章

引入技术

技术的增长终于可以解释生活水平的持续增长

劳动效率E
因此生产函数改写为
$Y=f(K,L\times E)$

其中 E 的增长率为 $g$

这里的技术增长引起的是等效劳动力的增长，即相同的人口实现等价于更多人口的效果
称为劳动改善型进步
（注意：这里有一点区别，这个等效人口要完全视为正常人口，其并没有改变资本的利用率，我个人认为这种增长的计算要在最后分配收入的时候，将本来要分配给等效人口的数量的收入分配给更少的实际人口，但后续的黄金律并不是这么考虑）

计算一切如故，最终结果为

稳态：
$\Delta k=sf(k)-(\delta +n+g)k$
$i=(\delta +n+g)k^{\ast }$

黄金律：
$c^{\ast }=y-i=f(k^{\ast })-(\delta +n+g)k$

$MPK=\delta +n+g$

注意是 $n+g$