考研数据结构(3)笔记
数据结构(1)链接https://blog.csdn.net/Z_timer/article/details/105595519(多图预警)
数据结构(2)链接https://blog.csdn.net/Z_timer/article/details/106457448
目录
树
树的定义
二叉树
求完全二叉树的高度、深度
一些性质
树与二叉树的转换
树转森林
树的遍历(该章节最上面的链接有)
递归
树的遍历
考点总结
线索二叉树
二叉树的估计
根据表达式建立二叉树
哈夫曼树
根据遍历序列画树
图
图的定义
图的遍历
最小生成树、最短路径、拓扑排序、关键路径
排序
堆排序
外部排序
查找
顺序查找
折半查找
分块查找
二叉排序树
平衡二叉树
B-、B+树
Hash表
算法分析
线性结构
非线性结构
汉诺塔问题
排序算法
树
考点: 遍历,结点数,森林与树的转换,线索树,树度和结点数,哈夫曼树,。。。。。
题目:https://blog.csdn.net/Z_timer/article/details/109599781?#t20 (可以把这个先放地址栏,有些知识在这些里面,下面一些知识就不多赘述了)
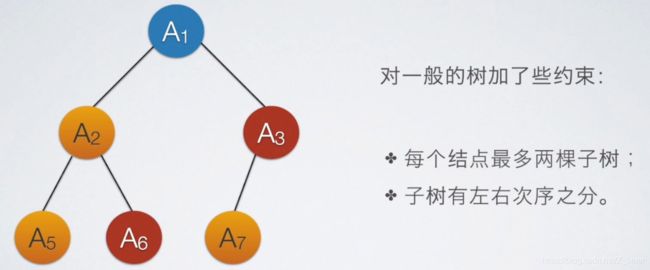
树的定义
一对多的关系
看书把 比较容易理解,以下摘自维基百科
树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 树的度:一棵树中,最大的节点度称为树的度;
- 叶节点或终端节点:度为零的节点;
- 非终端节点或分支节点:度不为零的节点;
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的逻辑结构和存储结构
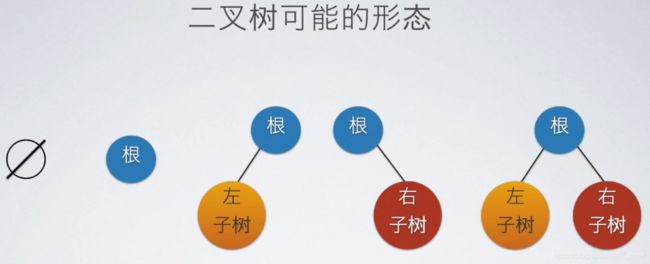
二叉树
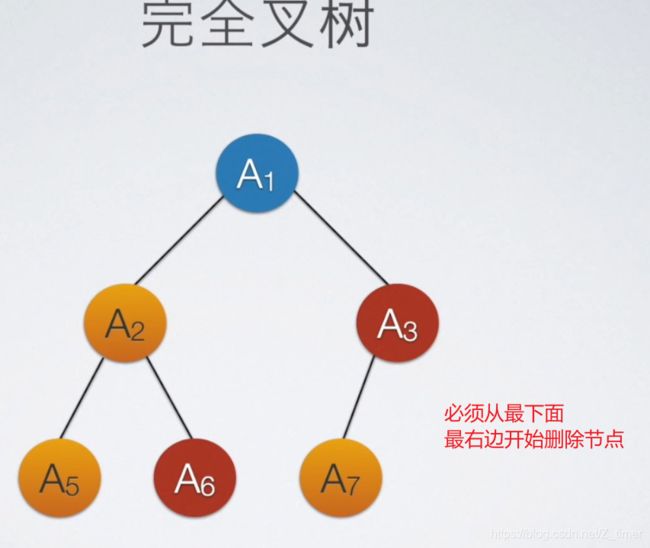
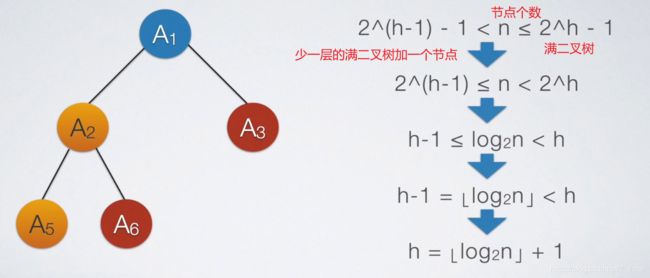
求完全二叉树的高度、深度
求高度一共就这两种,一般不会出现选项中没有这两种情况
一些性质
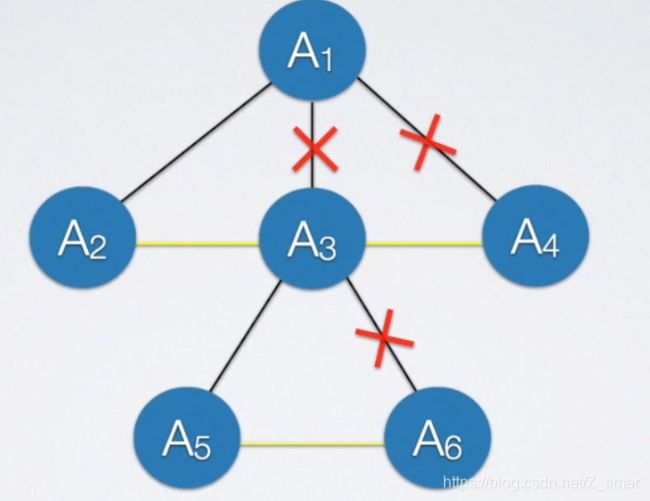
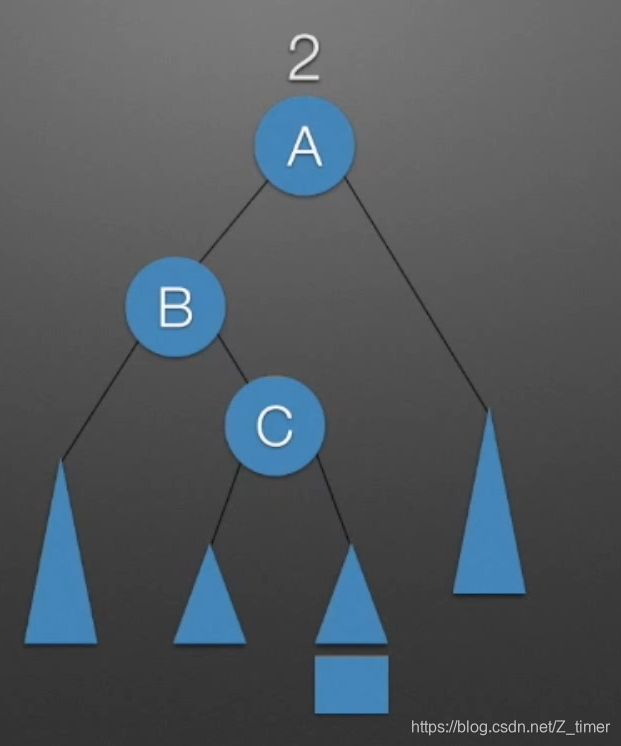
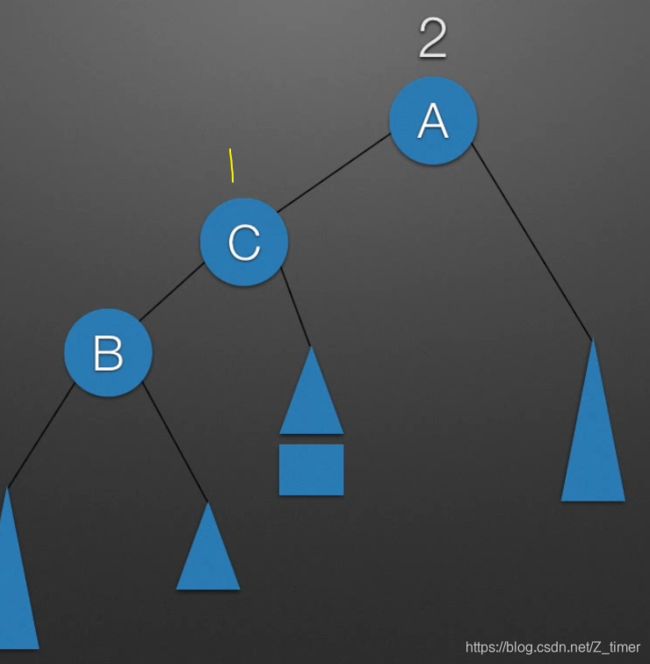
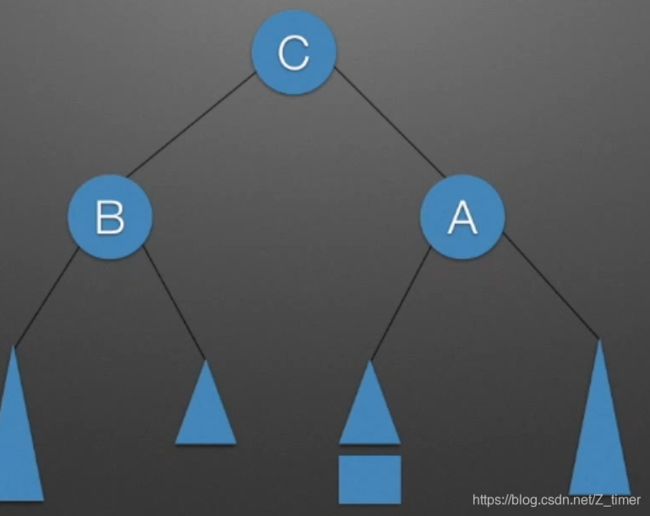
树与二叉树的转换
记住左孩右兄即可
树转森林
树的遍历(该章节最上面的链接有)
递归
https://lyl0724.github.io/2020/01/25/1/
进不去可以再刷新一下,感觉挺不错的
树的遍历
此节也不做讲述,对着图 看着代码一步步来进入函数内部应该能理解吧。
代码看这里https://blog.csdn.net/Z_timer/article/details/113814578#t1、非递归:https://www.cnblogs.com/dolphin0520/archive/2011/08/25/2153720.html
考点总结
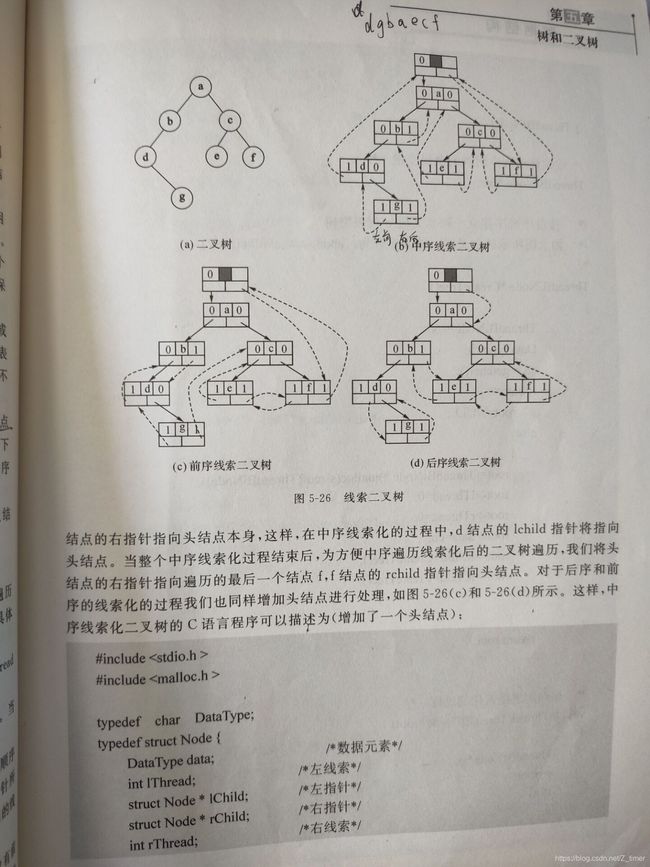
线索二叉树
二叉树的估计
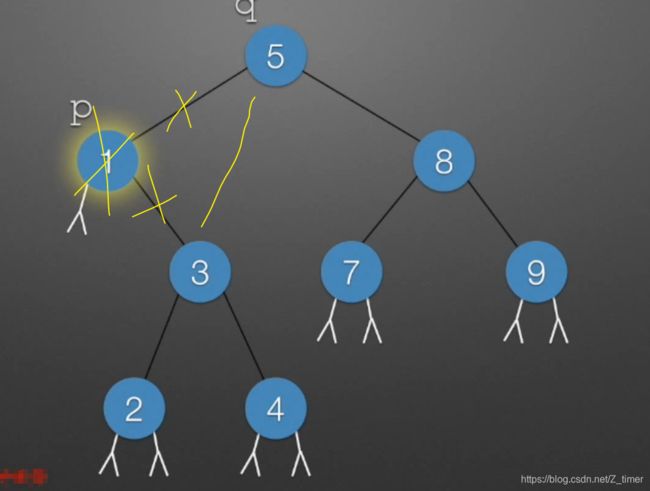
https://blog.csdn.net/Z_timer/article/details/109599781#t22 参考第35题,下面的图就是先把遍历后的结果抽象化,如前序遍历肯定是TLR,中序LTR,后序LRT,然后删除对应的分支令其结果一致即可。
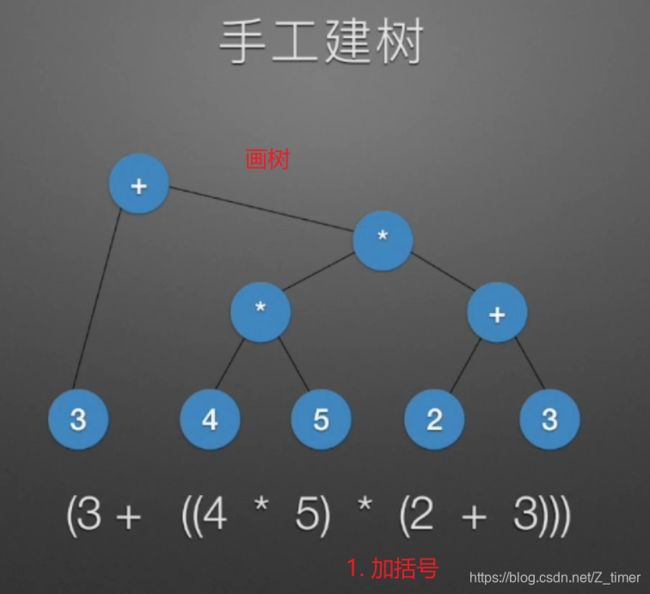
根据表达式建立二叉树
利用栈建树https://zhuanlan.zhihu.com/p/126296610
哈夫曼树
概念及代码:https://blog.csdn.net/google19890102/article/details/54848262
评价带权路径:https://blog.csdn.net/qq_29519041/article/details/81428934
题目: https://blog.csdn.net/Z_timer/article/details/109599781#t20,,,49、50、51题
我也不知道为啥 我自己感觉挺简单的 除了算平均带权路径可能会出错
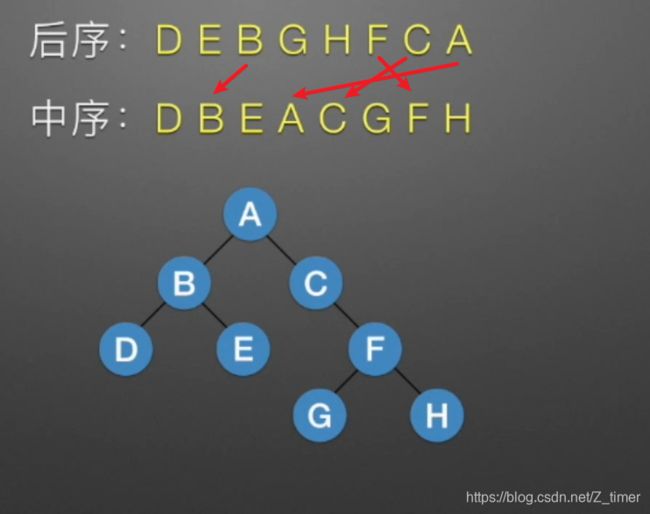
根据遍历序列画树
代码:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/
代码:https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/
图
图的定义
多对多的关系
https://blog.csdn.net/Z_timer/article/details/109330916
例题:
第二问:A2就是数学当中的矩阵乘,然后(0, 3)的含义就是因为
第0行代表从0到其他顶点哪些有边,同理。第3列到其他顶点哪些有变,而(0, 3)是根据对应行对应列相乘并且相加后得到的,(0, k)是下标 即Σ(A(0, k) × A(k, 3)) ,只有对应都为1相乘才为1,即通过k这个顶点可到3,最后相加就是3,这里可以看看天勤的数据结构图的部分
邻接表看出度,逆邻接表看入度
十字链表、邻接多重表
图的遍历
DFS就是尽可能沿着路径访问一条路径上的所有节点,直到该条路径不行再换条路走,BFS就是访问所有邻接点后再访问下一层节点。
代码自行百度或点击该链接。
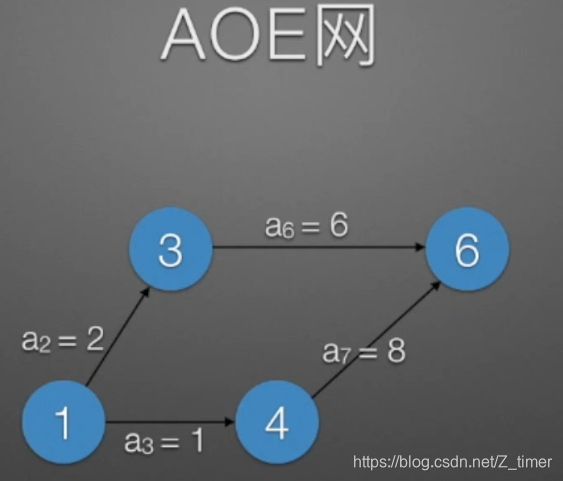
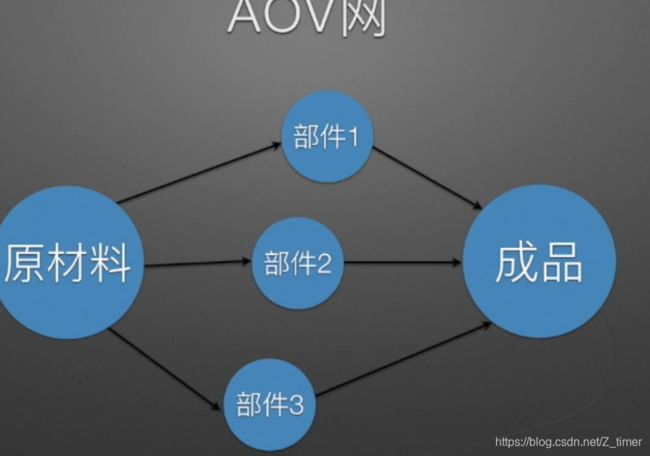
最小生成树、最短路径、拓扑排序、关键路径
此处参考大链接下的内容,总结的挺全了。
注意下拓扑排序和关键路径里的图怎么画,我非统考 忘记AOV和AOE怎么画了= = ,(AOV activity on vertex;AOE activity on edge)英语全写很清晰了
排序
日常贴链接:https://blog.csdn.net/Z_timer/article/details/109450846
题目:https://blog.csdn.net/Z_timer/article/details/110929131#t9
堆排序
其中的堆虽然跟二叉树差不多,但是其各个根节点必须大于或小于左右子分支。
外部排序
多路归并排序
置换选择排序http://data.biancheng.net/view/78.html
最佳归并树、败者树 http://data.biancheng.net/view/77.html
查找
题目:https://blog.csdn.net/Z_timer/article/details/110929131#t4
顺序查找
ASL1 = (1+2+3+4+5+6)/6 = 7/2 ; ASL(失败) = (7+7+7+7+7+7+7+7)/7 = 7
折半查找
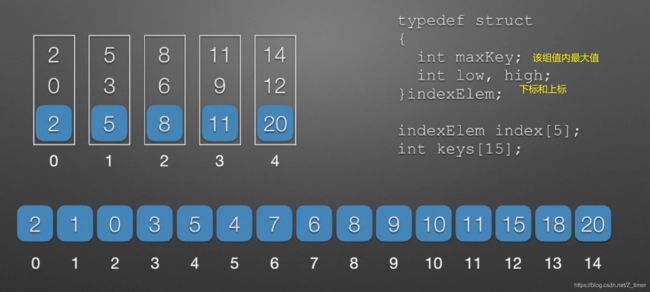
分块查找
二叉排序树
删除指针需要带一个父节点。
如果删除叶子节点,只需要令父节点将其置空。
如果删除单支节点的父节点,即没有左子树或者右子树,则把左右子树直接挂在父亲节点即可,取代原本的节点。
如果删除父节点,则可以到父节点的左孩子,然后一直往右走,因为右边都是比其所在分支的节点大,将最右边的节点赋值到父节点即可;或者右孩子然后一直往左走找到右子树的最小值,然后赋值给父节点。
平衡二叉树
LL和RR就不说了。
LR:给B的右子树进行形象化,即加一个C节点,然后拆分成两个子树,对BC所在树进行RR旋转,然后合并再用LL选择即可,RL同理 只不过取反。
注意无论怎么变,必须要保持平衡二叉树的性质和二叉排序树的性质,即左小右大,平衡因子为1。
B-、B+树
B(B-)、B+树的插入删除https://www.cnblogs.com/nullzx/p/8729425.html
注意阶数是人为规定的,其不会受到任何影响。如图选A,可能有人误认为5阶必须有个塞满四个空位即B 7
Hash表
注意:不同学校对失败ASL不一样。
构造方法:
直接定址法。
数字分析法:适用关键字位数比较多且表中可能的关键字都是已知的情况。分析的原则是尽量取冲突少的位数段
平方取中法:取关键字平方后的中间几位。
除留余数法:取不大于Hash表表长m的数p除后所得余数为地址。尽量取小于或者大于表长的最大素数
冲突处理:
开放地址法:线性探查法(探测所有位置,易产生堆积现象)、平方探测法(不可能探测表中所有位置,不易堆积)。
链地址法:相同关键字存在链表中
算法分析
线性结构
如果有序的话用折半查找时间复杂度为O(logn)
非线性结构
邻接矩阵遍历节点:O(n^2)、邻接表遍历节点:O(n+e)
Prim算法:O(n^2)、Kruskal算法:O(eloge)
Dijkstra算法:O(n^2)、Floyd算法:O(n^3)
汉诺塔问题
排序算法
快速排序
归并排序最好、最坏和平均情况下时间复杂度都为O(nlogn),空间复杂度为O(n)。
希尔排序(考研下的):
堆排序:建堆时间复杂度为O(n)
基数排序(记住就好):