NNDL 实验五前馈神经网络（2）自动梯度计算和优化问题

4.3 自动梯度计算

虽然我们能够通过模块化的方式比较好地对神经网络进行组装，但是每个模块的梯度计算过程仍然十分繁琐且容易出错。在深度学习框架中，已经封装了自动梯度计算的功能，我们只需要聚焦模型架构，不再需要耗费精力进行计算梯度。

飞桨提供了paddle.nn.Layer类，来方便快速的实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。继承了paddle.nn.Layer类的算子中，可以在内部直接调用其它继承paddle.nn.Layer类的算子，飞桨框架会自动识别算子中内嵌的paddle.nn.Layer类算子，并自动计算它们的梯度，并在优化时更新它们的参数。

pytorch中的相应内容是什么？请简要介绍。
对应torch中的torch.nn.Module，它是所有神经网络模型的基类，当你想自定义一个神经网络时，需要继承这个类，用类似以下结构来实现：

import torch.nn as nn
import torch.nn.functional as F

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Conv2d(1, 20, 5)# submodule: Conv2d
        self.conv2 = nn.Conv2d(20, 20, 5)

    def forward(self, x):
       x = F.relu(self.conv1(x))
       return F.relu(self.conv2(x))

(来自官方文档）
与paddle一样，torch也支持自动求导机制，通过自动求导进行参数更新。对于复杂的神经网络，可以避免因手动公式推导带来的各种繁琐与失误，对于神经网络的发展有积极作用，增大了设计的上限。对于底层的torch自动求导实现，以后会有深入的学习。现将目光聚焦于网络的设计部分。

4.3.1 利用预定义算子重新实现前馈神经网络

使用Paddle的预定义算子来重新实现二分类任务。主要使用到paddle.nn.Linear。
为提高对比的直观性，现添加代码实现参数和结果的可视化。

数据集选用双月数据集。

使用pytorch的预定义算子来重新实现二分类任务。（必做）

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]


class LogisticClassification(nn.Module):
    def __init__(self):
        super(LogisticClassification, self).__init__()
        self.linear = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        pre_y = self.sigmoid(x1)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    net = LogisticClassification()
    train_data, verify_data, test_data=get_moon_data()
    X=train_data[0];y=train_data[1]
    epoches=5000
    loss_list=[]
    for i in range(epoches):
        loss = nn.BCELoss()
        optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
        pre_y = net(X)
        l = loss(pre_y, y)
        optimizer.zero_grad()  # 梯度清零
        l.backward()
        optimizer.step()
        loss_list.append(l.item())
        if i%10==0:
            print('epoch %d, loss: %f' % (i, l.item()))
            net.save_model('LNet.pt')
            print('Current acc in verify data:',acc(net,verify_data[0],verify_data[1])*100,'%')
    print('acc in test data :',acc(net,test_data[0],test_data[1])*100,'%')
    x=range(epoches)
    plt.plot(x,loss_list)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.show()

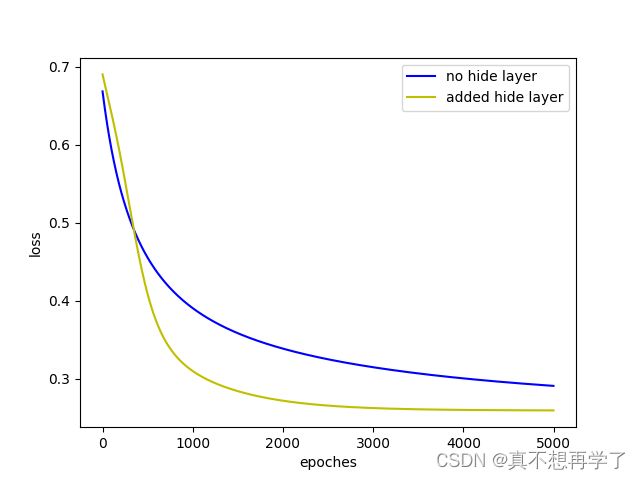
增加一个3个神经元的隐藏层，再次实现二分类，并与1做对比。（必做）

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]


class LogisticClassification1(nn.Module):
    def __init__(self):
        super(LogisticClassification1, self).__init__()
        self.linear = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        pre_y = self.sigmoid(x1)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification2(nn.Module):
    def __init__(self):
        super(LogisticClassification2, self).__init__()
        self.linear = nn.Linear(2, 3)
        self.hide=nn.Linear(3,1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2=self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    labels=['no hide layer','added hide layer']
    c=['b','y']
    plt.figure()
    train_data, verify_data, test_data=get_moon_data()
    X=train_data[0];y=train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2()]):
        epoches=5000
        loss_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('Current acc in verify data:',acc(net,verify_data[0],verify_data[1])*100,'%')
        print('acc in test data :',acc(net,test_data[0],test_data[1])*100,'%')
        x=range(epoches)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.legend()
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.show()

从图像可以明显看出加了隐藏层的模型的损失要小于不加隐藏层的模型。

再加上对正确率的绘图，运行速度明显变慢了。

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]


class LogisticClassification1(nn.Module):
    def __init__(self):
        super(LogisticClassification1, self).__init__()
        self.linear = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        pre_y = self.sigmoid(x1)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification2(nn.Module):
    def __init__(self):
        super(LogisticClassification2, self).__init__()
        self.linear = nn.Linear(2, 3)
        self.hide=nn.Linear(3,1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2=self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    labels=['no hide layer','added hide layer']
    c=['b','y']
    plt.figure()
    train_data, verify_data, test_data = get_moon_data()
    X = train_data[0];
    y = train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2()]):
        epoches=5000
        loss_list=[]
        acc_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('acc in test data :', acc(net, test_data[0], test_data[1]) * 100, '%')
            acc_list.append(acc(net, test_data[0], test_data[1]) * 100)
        print('Current acc in verify data:', acc(net, verify_data[0], verify_data[1]) * 100, '%')
        x=range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list,c=c[j],label=labels[j])
        plt.subplot(1, 2, 2)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.subplot(1,2,1)
    plt.xlabel('epoches')
    plt.ylabel('acc(%)')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.legend()
    plt.show()

5. 自定义隐藏层层数和每个隐藏层中的神经元个数，尝试找到最优超参数完成二分类。可以适当修改数据集，便于探索超参数。（选做）

为提高测试的效率，从这里开始先将学习率lr由0.01增加到0.1，迭代次数由5000降低到2000。同时为增强对比性，再次添加了一个三层3个神经元的神经网络作为对照，并对颜色进行了调整。

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]


class LogisticClassification1(nn.Module):
    def __init__(self):
        super(LogisticClassification1, self).__init__()
        self.linear = nn.Linear(2, 3)
        self.hide = nn.Linear(3, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2 = self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification2(nn.Module):
    def __init__(self):
        super(LogisticClassification2, self).__init__()
        self.linear = nn.Linear(2,3)
        self.hide1=nn.Linear(3,3)
        self.hide2=nn.Linear(3,1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2=self.hide1(x1)
        x2=self.sigmoid(x2)
        x3=self.hide2(x2)
        pre_y = self.sigmoid(x3)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification3(nn.Module):
    def __init__(self):
        super(LogisticClassification3, self).__init__()
        self.linear = nn.Linear(2,3)
        self.hide1=nn.Linear(3,3)
        self.hide2=nn.Linear(3,3)
        self.hide3 = nn.Linear(3, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2=self.hide1(x1)
        x2=self.sigmoid(x2)
        x3=self.hide2(x2)
        x3=self.sigmoid(x3)
        x4=self.hide3(x3)
        pre_y = self.sigmoid(x4)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    labels=['1  hide layer','2  hide layers','3  hide layers']
    c=['#006463','#00bcba','#98fffe']
    plt.figure()
    train_data, verify_data, test_data=get_moon_data()
    X=train_data[0];y=train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2(),LogisticClassification3()]):
        epoches=2000
        loss_list=[]
        acc_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('acc in test data :', acc(net, test_data[0], test_data[1]) * 100, '%')
            acc_list.append(acc(net, test_data[0], test_data[1]) * 100)
        print('Current acc in verify data:', acc(net, verify_data[0], verify_data[1]) * 100, '%')
        x=range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list,c=c[j],label=labels[j])
        plt.subplot(1, 2, 2)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.subplot(1,2,1)
    plt.xlabel('epoches')
    plt.ylabel('acc(%)')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.legend()
    plt.show()

由图像可以看出，隐藏层的个数影响了均方误差loss的下降，当隐藏层数目增多时，loss突降的迭代次数会延后。同时隐藏层个数也影响着正确率的上升，隐藏层越多，达到最高值的迭代次数也延后，并且最后acc收敛时的正确率越高。
但是这里出现了一个问题，当我再一次运行时：

损失下降的符合预期，正确率acc达到最高值的迭代次数也符合预期，但是最高值分布和上一次的结果完全相反。
推测原因是没有保持数据集一致，因为我是每次训练一个神经网络都生成了一次数据集，下边做了修改，只生成一次数据集。只部分修改了主函数。

if __name__ == '__main__':
    labels=['1  hide layer','2  hide layers','3  hide layers']
    c=['#006463','#00bcba','#98fffe']
    plt.figure()
    train_data, verify_data, test_data = get_moon_data()
    X = train_data[0];
    y = train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2(),LogisticClassification3()]):
        epoches=2000
        loss_list=[]
        acc_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('acc in test data :', acc(net, test_data[0], test_data[1]) * 100, '%')
            acc_list.append(acc(net, test_data[0], test_data[1]) * 100)
        print('Current acc in verify data:', acc(net, verify_data[0], verify_data[1]) * 100, '%')
        x=range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list,c=c[j],label=labels[j])
        plt.subplot(1, 2, 2)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.subplot(1,2,1)
    plt.xlabel('epoches')
    plt.ylabel('acc(%)')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.legend()
    plt.show()

第一次运行：

第二次运行：

结果具有了共性，这次可以放心分析了。
和上面分析的一样，隐藏层个数增多延后了损失的突降，延后了正确率acc的陡增，和之前不一样的是，最后收敛到的正确率和损失值是趋于一致的。
就在我得出以上结论后，意外又发生了。

如图，当我再一次重复运行时候，3隐藏层的神经网络出现了这种情况，他的正确率在一开始陡增到50%后停止了提高，损失则在一开始几乎不下降，到了2000次左右才开始下降一点点。
推测可能是迭代次数的不够，后面可能会有三隐藏层损失的突降以及正确率的陡增。因为参考前两个结果，他们的三隐藏层也有这种倾向。暂时不知道是什么原因。
最后再运行一次：

非常符合预期。
结论：
隐藏层个数增多延后了损失的突降，延后了正确率acc的陡增，并且最后收敛到的正确率和损失值是不变的。

下面再尝试一次增加神经元的个数：
分别为3，10，20，50

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]


class LogisticClassification1(nn.Module):
    def __init__(self):
        super(LogisticClassification1, self).__init__()
        self.linear = nn.Linear(2, 3)
        self.hide = nn.Linear(3, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2 = self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification2(nn.Module):
    def __init__(self):
        super(LogisticClassification2, self).__init__()
        self.linear = nn.Linear(2, 10)
        self.hide = nn.Linear(10, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2 = self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification3(nn.Module):
    def __init__(self):
        super(LogisticClassification3, self).__init__()
        self.linear = nn.Linear(2, 20)
        self.hide = nn.Linear(20, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2 = self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification4(nn.Module):
    def __init__(self):
        super(LogisticClassification4, self).__init__()
        self.linear = nn.Linear(2, 50)
        self.hide = nn.Linear(50, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        x2 = self.hide(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    labels=['3 neuron hide layer','10 neuron hide layer','20 neuron hide layer','50 neuron hide layer']
    c=['#006463','#00bcba','#00fffc','#98fffe']
    plt.figure()
    train_data, verify_data, test_data = get_moon_data()
    X = train_data[0];
    y = train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2(),LogisticClassification3(),LogisticClassification4()]):
        epoches=1000
        loss_list=[]
        acc_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('acc in test data :', acc(net, test_data[0], test_data[1]) * 100, '%')
            acc_list.append(acc(net, test_data[0], test_data[1]) * 100)
        print('Current acc in verify data:', acc(net, verify_data[0], verify_data[1]) * 100, '%')
        x=range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list,c=c[j],label=labels[j])
        plt.subplot(1, 2, 2)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.subplot(1,2,1)
    plt.xlabel('epoches')
    plt.ylabel('acc(%)')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.legend()
    plt.show()

发现隐藏层神经元数增多会提前损失的突降和正确率的陡增。并且这里可以很明显的观察到过拟合现象，正确率再上升到一定程度后又下降了。
为更加细致的观察，将迭代次数降低到700又运行了一次。

为避免结果的偶然性，再次运行了一次。

又运行了一次：

可见结果基本符合预期。
增加隐含层数会延后并延缓突变，增加神经元数会提前并加快突变，那么将这两个结合起来是不是就会抵消这个问题呢。
接下来同时增加隐藏层数和神经元数。

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]



class LogisticClassification1(nn.Module):
    def __init__(self):
        super(LogisticClassification1, self).__init__()
        self.hide = nn.Linear(2, 3)
        self.linear = nn.Linear(3, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.hide(x)
        x2 = self.linear(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification2(nn.Module):
    def __init__(self):
        super(LogisticClassification2, self).__init__()
        self.hide1 = nn.Linear(2, 20)
        self.hide2 = nn.Linear(20, 20)
        self.linear = nn.Linear(20, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.hide1(x)
        x1 = self.sigmoid(x1)
        x2 = self.hide2(x1)
        x2 = self.sigmoid(x2)
        x3=self.linear(x2)
        pre_y=self.sigmoid(x3)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification3(nn.Module):
    def __init__(self):
        super(LogisticClassification3, self).__init__()
        self.hide1 = nn.Linear(2, 50)
        self.hide2=nn.Linear(50,50)
        self.hide3=nn.Linear(50,50)
        self.linear = nn.Linear(50, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.hide1(x)
        x1 = self.sigmoid(x1)
        x2 = self.hide2(x1)
        x2=self.sigmoid(x2)
        x3=self.hide3(x2)
        x3=self.sigmoid(x3)
        x4=self.linear(x3)
        pre_y = self.sigmoid(x4)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    labels=['1 hide layer of 3 neuron','2 hide layer of 20 neuron','3 hide layer of 50 neuron']
    c=['#006463','#00bcba','#00fffc']
    plt.figure()
    train_data, verify_data, test_data = get_moon_data()
    X = train_data[0];
    y = train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2(),LogisticClassification3()]):
        epoches=2000
        loss_list=[]
        acc_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('acc in test data :', acc(net, test_data[0], test_data[1]) * 100, '%')
            acc_list.append(acc(net, test_data[0], test_data[1]) * 100)
        print('Current acc in verify data:', acc(net, verify_data[0], verify_data[1]) * 100, '%')
        x=range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list,c=c[j],label=labels[j])
        plt.subplot(1, 2, 2)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.subplot(1,2,1)
    plt.xlabel('epoches')
    plt.ylabel('acc(%)')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.legend()
    plt.show()

第一次运行：

第二次运行：

解决了一点点，但是没有完全解决。我们发现隐藏层数似乎是影响突变位置的主要因素，另一种可能是神经元数不够多。
下面调高隐藏层神经元数目。
这次运行时间明显变长了。最后一个神经网络迭代20次将近用了一秒钟。

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]



class LogisticClassification1(nn.Module):
    def __init__(self):
        super(LogisticClassification1, self).__init__()
        self.hide = nn.Linear(2, 3)
        self.linear = nn.Linear(3, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.hide(x)
        x2 = self.linear(x1)
        pre_y = self.sigmoid(x2)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification2(nn.Module):
    def __init__(self):
        super(LogisticClassification2, self).__init__()
        self.hide1 = nn.Linear(2, 200)
        self.hide2 = nn.Linear(200, 200)
        self.linear = nn.Linear(200, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.hide1(x)
        x1 = self.sigmoid(x1)
        x2 = self.hide2(x1)
        x2 = self.sigmoid(x2)
        x3=self.linear(x2)
        pre_y=self.sigmoid(x3)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

class LogisticClassification3(nn.Module):
    def __init__(self):
        super(LogisticClassification3, self).__init__()
        self.hide1 = nn.Linear(2, 500)
        self.hide2=nn.Linear(500,500)
        self.hide3=nn.Linear(500,500)
        self.linear = nn.Linear(500, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.hide1(x)
        x1 = self.sigmoid(x1)
        x2 = self.hide2(x1)
        x2=self.sigmoid(x2)
        x3=self.hide3(x2)
        x3=self.sigmoid(x3)
        x4=self.linear(x3)
        pre_y = self.sigmoid(x4)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

def acc(model, X, y):
    '''最大项的为预测的类别'''
    ct=0
    for i in range(len(y)):
        pre_y = model(X[i])
        if pre_y>=0.5:
            pre_y=1
        else:pre_y=0
        if pre_y==y[i]:
            ct+=1
    return ct/y.shape[0]

if __name__ == '__main__':
    labels=['1 hide layer of 3 neuron','2 hide layer of 200 neuron','3 hide layer of 500 neuron']
    c=['#006463','#00bcba','#00fffc']
    plt.figure()
    train_data, verify_data, test_data = get_moon_data()
    X = train_data[0];
    y = train_data[1]
    for j,net in enumerate([LogisticClassification1(),LogisticClassification2(),LogisticClassification3()]):
        epoches=2000
        loss_list=[]
        acc_list=[]
        for i in range(epoches):
            loss = nn.BCELoss()
            optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i%10==0:
                print('epoch %d, loss: %f' % (i, l.item()))
                net.save_model('LNet.pt')
                print('acc in test data :', acc(net, test_data[0], test_data[1]) * 100, '%')
            acc_list.append(acc(net, test_data[0], test_data[1]) * 100)
        print('Current acc in verify data:', acc(net, verify_data[0], verify_data[1]) * 100, '%')
        x=range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list,c=c[j],label=labels[j])
        plt.subplot(1, 2, 2)
        plt.plot(x,loss_list,c=c[j],label=labels[j])
    plt.subplot(1,2,1)
    plt.xlabel('epoches')
    plt.ylabel('acc(%)')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.xlabel('epoches')
    plt.ylabel('loss')
    plt.legend()
    plt.show()

第一次运行：

第二次运行：

最后结果是这样，相对于之前，达到收敛需要的迭代次数明显减少了。上次2000次还没达到收敛，这次只用了1000次就基本上收敛了。可见，对于层数较多神经网络，我们可以通过增加神经元个数来加速收敛。

4.3.2 完善Runner类

为Runner类添加Visible_LogisticClassification_train，可视化训练，但是这个方法运行很慢。可以考虑多进程，但是吃配置，而且作者还不熟练。

# coding:utf-8

import torch
import torch.nn as nn
from torch import optim
import matplotlib.pyplot as plt

class Runner_V2():

    def __init__(self,model,lossfunc,optim):
        '''传入模型、损失函数、优化器和评价指标'''
        self.model=model
        self.loss=lossfunc
        self.optim=optim

    def SoftmaxClassify_train(self,X,y,epoches=500):
        print('start training....')
        for i in range(epoches):
            loss = self.loss
            optimizer = self.optim
            pre_y = self.model(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            if i % 50 == 0:
                print('epoch %d, loss: %f' % (i, l.item()))
        print('training ended.')

        def Visible_LogisticClassification_train(self,X,y,epoches=500):
        print('start training....')
        net = self.model
        loss_list = []
        acc_list=[]
        for i in range(epoches):
            loss = self.loss
            optimizer = self.optim
            pre_y = net(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            loss_list.append(l.item())
            if i % 10 == 0:
                print('epoch %d, loss in train data: %f' % (i, l.item()))
                net.save_model('LNet.pt')
            acc_list.append(self.LogisticClassify_acc(X,y))
        x = range(epoches)
        plt.subplot(1,2,1)
        plt.plot(x,acc_list)
        plt.xlabel('epoches')
        plt.ylabel('acc(%)')
        plt.subplot(1,2,2)
        plt.plot(x, loss_list)
        plt.xlabel('epoches')
        plt.ylabel('loss')
        plt.show()
        print('training ended.')

    def LosgisticCliassify_train(self,X,y,epoches=500):
        print('start training....')
        for i in range(epoches):
            loss = self.loss
            optimizer = self.optim
            pre_y = self.model(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            if i % 50 == 0:
                print('epoch %d, loss: %f' % (i, l.item()))
        print('training ended.')

    def LSM_train(self,X,y,epoches=500):
        '''train_data:列表类型，两个元素为tensor类型，第一个是x，第二个是y'''
        print('start training....')
        model=self.model
        loss = self.loss
        optimizer = self.optim
        num_epochs = epoches
        for epoch in range(num_epochs):
            pre_y = model(X)
            l = loss(pre_y, y)
            optimizer.zero_grad()  # 梯度清零
            l.backward()
            optimizer.step()
            print('epoch %d, loss: %f' % (epoch, l.item()))
        print('training ended.')

    def LSM_evaluate(self,X,y):
        '''测试模型
        test_data:列表类型，两个元素为tensor类型，第一个是x，第二个是y'''
        l = self.loss(self.model(X), y)
        print('loss in test data:', l.item())

    def predict(self,X):
        '''预测数据'''
        return self.model(X)

    def save_model(self, save_path):
        ''''.pt'文件'''
        torch.save(self, save_path)

    def read_model(self, path):
        ''''.pt'文件'''
        torch.load(path)

    def LogisticClassify_acc(self, X, y):
        '''最大项的为预测的类别'''
        ct = 0
        for i in range(len(y)):
            pre_y = self.model(X[i])
            if pre_y >= 0.5:
                pre_y = 1
            else:
                pre_y = 0
            if pre_y == y[i]:
                ct += 1
        return ct / y.shape[0]

    def SoftmaxClassify_acc(self, X, y):
        pre_y = self.model(X)
        max_pre_y = torch.argmax(pre_y, dim=1)
        max_y = torch.argmax(y, dim=1)
        return torch.nonzero(max_y.eq(max_pre_y)).shape[0] / y.shape[0]

4.3.3 模型训练

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch.nn as nn
import torch.optim as optim
import torch
import numpy as np
from Runner_V2 import *

def get_moon_data():
    X, y = make_moons(1000, noise=0.1)
    '''plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()'''
    X=torch.from_numpy(X.astype(np.float32))
    y=torch.from_numpy(y.astype(np.float32)).reshape(len(y),1)
    '''将1000条样本数据拆分成训练集、验证集和测试集，其中训练集640条、验证集160条、测试集200条。'''
    train_X,verify_X,test_X=torch.split(X,[640,160,200])
    train_y, vertify_y, test_y = torch.split(y, [640, 160, 200])
    return [train_X,train_y],[verify_X,vertify_y],[test_X,test_y]


class LogisticClassification(nn.Module):
    def __init__(self):
        super(LogisticClassification, self).__init__()
        self.linear = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x1 = self.linear(x)
        pre_y = self.sigmoid(x1)
        return pre_y

    def save_model(self, save_path):
        torch.save(self, save_path)

    def read_model(self, path):
        torch.load(path)

if __name__ == '__main__':
    net = LogisticClassification()
    train_data, verify_data, test_data=get_moon_data()
    X=train_data[0];y=train_data[1]
    loss = nn.BCELoss()
    optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
    runner=Runner_V2(model=net,lossfunc=loss,optim=optimizer)
    runner.Visible_LogisticClassification_train(X,y,epoches=5000)

4.3.4 性能评价

	acc=runner.LogisticClassify_acc(test_data[0],test_data[1])
    print('acc in test data:',acc*100,'%')

acc in test data: 89.5 %

4.4 优化问题

4.4.1 参数初始化

实现一个神经网络前，需要先初始化模型参数。

如果对每一层的权重和偏置都用0初始化，那么通过第一遍前向计算，所有隐藏层神经元的激活值都相同；在反向传播时，所有权重的更新也都相同，这样会导致隐藏层神经元没有差异性，出现对称权重现象。

如果权重初始值都为0，那么网络中的每个神经元都计算出同样的输出，然后它们就会在反向传播中计算出同样的梯度，从而进行同样的参数更新。那么这样一个具有很多隐藏单元的网络结构就是完全多余的表达，最终该网络只能学到一种特征。这种现象称为：对称权重（Symmetric ways）

所有权重相同的问题称为对称权重（Symmetric ways），随机初始化解决的就是如何打破这种对称性。

之前的实验过程中分析过pytorch模型的参数初始化问题：

self.weight = Parameter(torch.empty((out_features, in_features), **factory_kwargs))

在Linear源代码中的这句话就是随机初始化参数的过程。实际上避免了对称权重的问题。

4.4.2 梯度消失问题

在神经网络的构建过程中，随着网络层数的增加，理论上网络的拟合能力也应该是越来越好的。但是随着网络变深，参数学习更加困难，容易出现梯度消失问题。

由于Sigmoid型函数的饱和性，饱和区的导数更接近于0，误差经过每一层传递都会不断衰减。当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练，这就是所谓的梯度消失问题。
在深度神经网络中，减轻梯度消失问题的方法有很多种，一种简单有效的方式就是使用导数比较大的激活函数，如：ReLU。

更详细一些的解释：
经过前面公式的推导，我们知道模型参数的每一层更新都需要他的后一层的参数，也就是说，他的参数更新是逐层递进的，我们还知道，sigmoid函数的导数在小于-5 和大于5的部分是极小的，趋于0 的，那么这种参数的更新计算导数时会损失掉一部分大小。隐藏层数少的时候这种损失不明显，而当隐藏层数多的时候，这种损失会变得愈发明显，导数会越叠加越小，当传递到前面几层时，导数已经小到了忽略不计的程度，那么这个时候，前面的参数就没办法进行更新，造成了梯度消失的问题。
所以为了避免这个问题，在设计层数很多的神经网络时，要避免使用类似Sigmoid函数这种激活函数，而是选择导数更大的激活函数，从而避免梯度消失现象。

Sigmoid函数与Relu函数的对比

import numpy as np
import math
import matplotlib.pyplot as plt

def Logistic(x):
    return 1/(1+math.e**(-x))

def Relu(X):
    n_x = []
    for i in X:
        n_x.append(max(0, i))
    return n_x


def d_Relu(X):
    n_x = []
    for i in X:
        if i<0:
            n_x.append(0)
        else:
            n_x.append(1)
    return n_x

def d_Sigmoid(X):
    return Logistic(X)*(1-Logistic(X))

if __name__=='__main__':
    x=np.linspace(-10,10,50)
    plt.figure()
    plt.subplot(1,2,1)
    plt.plot(x,Relu(x),c='r',label='Relu')
    plt.plot(x,Logistic(x),c='y',label='sigmoid')
    plt.grid()
    plt.legend()
    plt.subplot(1,2,2)
    plt.plot(x, d_Relu(x), c='r', label='grad of Relu')
    plt.plot(x, d_Sigmoid(x), c='y', label='grad of sigmoid')
    plt.grid()
    plt.legend()
    plt.show()

补充：这里的Relu函数求导的grad of Relu 小于零的部分实际上是不存在的，因为对0求导无意义。

4.4.3 死亡ReLU问题

ReLU激活函数可以一定程度上改善梯度消失问题，但是在某些情况下容易出现死亡ReLU问题，使得网络难以训练。

这是由于当x<0时，ReLU函数的输出恒为0。在训练过程中，如果参数在一次不恰当的更新后，某个ReLU神经元在所有训练数据上都不能被激活（即输出为0），那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远都不能被激活。

一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU的变种。
几种激活函数都比较：

import numpy as np
import math
import matplotlib.pyplot as plt

def Logistic(x):
    return 1/(1+math.e**(-x))

def Relu(X):
    n_x = []
    for i in X:
        n_x.append(max(0, i))
    return n_x

def leakyRelu(X,leak=0.3):
    n_x=[]
    for i in X:
        n_x.append(max(0,i)+min(0,i*leak))
    return n_x

def elu(X,r=0.3):
    n_x = []
    for i in X:
        n_x.append(max(0,i)+min(0,r*(math.e**i-1)))
    return n_x

def d_Relu(X):
    n_x = []
    for i in X:
        if i<0:
            n_x.append(0)
        else:
            n_x.append(1)
    return n_x

def d_Sigmoid(X):
    return X*(1-X)

def d_leakyRelu(X,leak=0.5):
    n_x=[]
    for i in X:
        if i<0:
            n_x.append(leak)
        else:
            n_x.append(1)
    return n_x

def d_elu(X,a=0.5):
    n_x=[]
    for i in X:
        if i<0:
            n_x.append(a*math.e**i-a)
        else:
            n_x.append(1)
    return n_x
if __name__=='__main__':
    x=np.linspace(-10,10,50)
    plt.figure()
    plt.subplot(1,2,1)
    plt.plot(x,Relu(x),c='r',label='Relu')
    plt.plot(x,leakyRelu(x),c='y',label='leakyRelu leak=0.5')
    plt.plot(x,elu(x), c='g', label='elu a=0.5')
    plt.grid()
    plt.legend()
    plt.subplot(1,2,2)
    plt.plot(x,d_Relu(x),c='r',label='grad of Relu')
    plt.plot(x,d_leakyRelu(x),c='y',label='grad of leakyRelu leak=0.5')
    plt.plot(x,d_elu(x), c='g', label='grad of elu a=0.5' )
    plt.grid()
    plt.legend()
    plt.show()