算法 - 单调栈
定义
从栈底元素到栈顶元素呈单调递增或单调递减,栈内序列满足单调性的栈。
适用问题
单调栈分为单调递增栈和单调递减栈,通过使用单调栈我们可以访问到下一个比他大(小)的元素(或者说可以)。也就是说在队列或数组中,我们需要通过比较前后元素的大小关系来解决问题时我们通常使用单调栈。
题目一
数组中的下个比当前大的节点
示例 1:
输入:[2,1,5]
输出:[5,5,0]
示例 2:
输入:[2,7,4,3,5]
输出:[7,0,5,5,0]
示例 3:
输入:[1,7,5,1,9,2,5,1]
输出:[7,9,9,9,0,5,0,0]
说明:
对于链表中的每个节点,1 <= node.val <= 10^9
给定列表的长度在 [0, 10000] 范围内
思路
- 双层循环,效率太低。
- 采用一个单调栈,栈里面的元素从栈顶到栈底部单调递增,遍历数组
- 如果栈为空,则直接进栈
- 如果不为空,
- 当前元素小于栈顶元素,直接进栈
- 当前元素大于栈顶元素,输出当前元素,栈顶出站,把当前元素的下标进栈
解法
#include
#include
#include
using namespace std;
vector getNextLargeNumber(vector& v) {
vector ret(v.size(), 0); //必须先初始化为0
stack s;
for(int i = 0; i < v.size(); i++) {
while(!s.empty() && v[s.top()] < v[i]) {
ret[s.top()] = v[i]; // 主要这里不是push_back
s.pop();
}
s.push(i);
}
return ret;
}
int main() {
vector vec{1,7,2,3,9,2,5,1};
vector ret = getNextLargeNumber(vec);
for (auto &i: ret) {
cout << i << ", ";
}
cout < 其他题目
- 柱状图中最大的矩形(单调栈)
给定一个含有若干个整数的数字,表示这些矩形的高度,要求返回能找到的面积最大的矩形的面积。
要求时间复杂度O(n)
示例
Input: [2,1,5,6,2,3]
Output: 10思路: 单调栈的解法(比较难理解)。。。。
把能完全包含各个柱状图的矩形的最大面积求出来,然后求出其中最大值即可。
如何求以某个柱子为高的最大矩形?
矩形的面积=高*宽。
我们很高兴的发现,在这个分支情况下,我们已经知道高了,那么宽度如何求呢?
通过观察,我们发现矩形的左边沿是左边第一个高比2小的柱子,右边沿是右边第一个高比2小的柱子(将高为3的柱子的右面看作还有一个高为0的柱子),问题转化为求当期柱子左右2边最小的柱子。
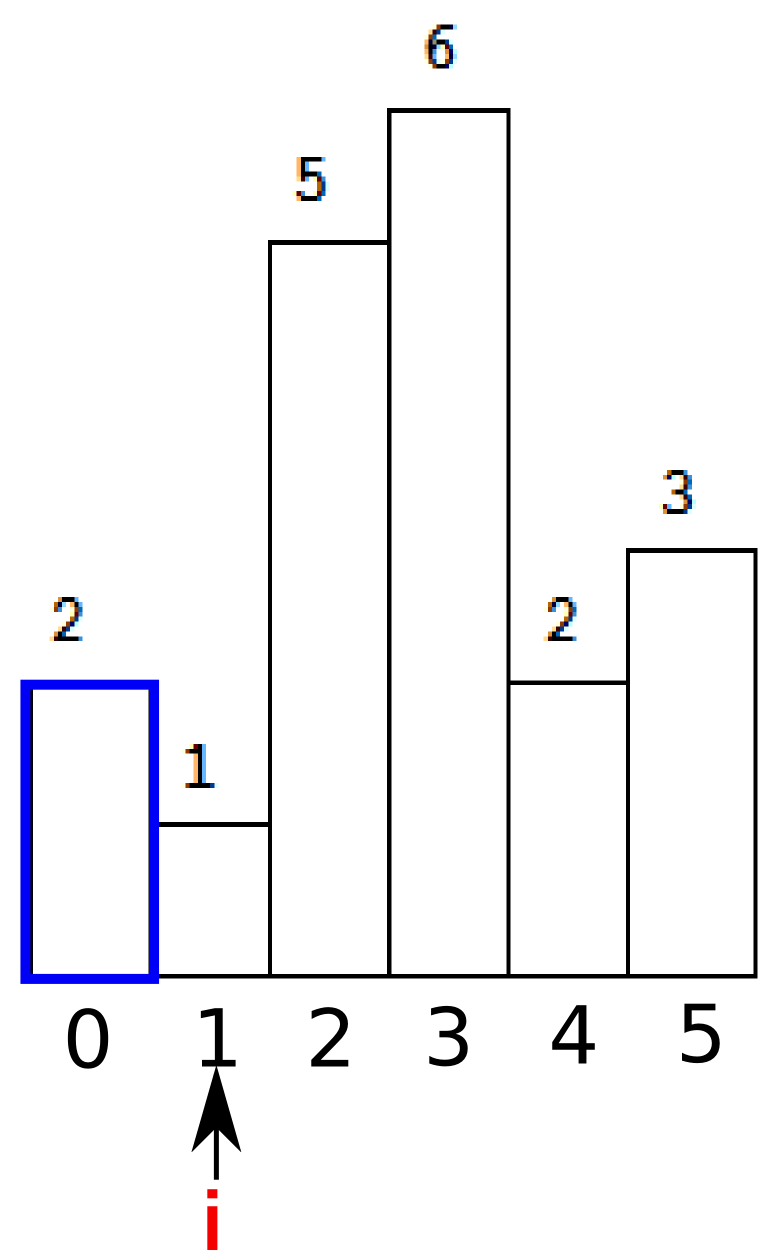
首先,如果栈是空的,那么索引i入栈。那么第一个i=0就进去吧。注意栈内保存的是索引,不是高度。然后i++。
然后继续,当i=1的时候,发现h[i]小于了栈内的元素,于是出栈。(由此可以想到,哦,看来stack里面只存放单调递增的索引)
这时候stack为空,所以面积的计算是h[t] * i.t是刚刚弹出的stack顶元素。也就是蓝色部分的面积。
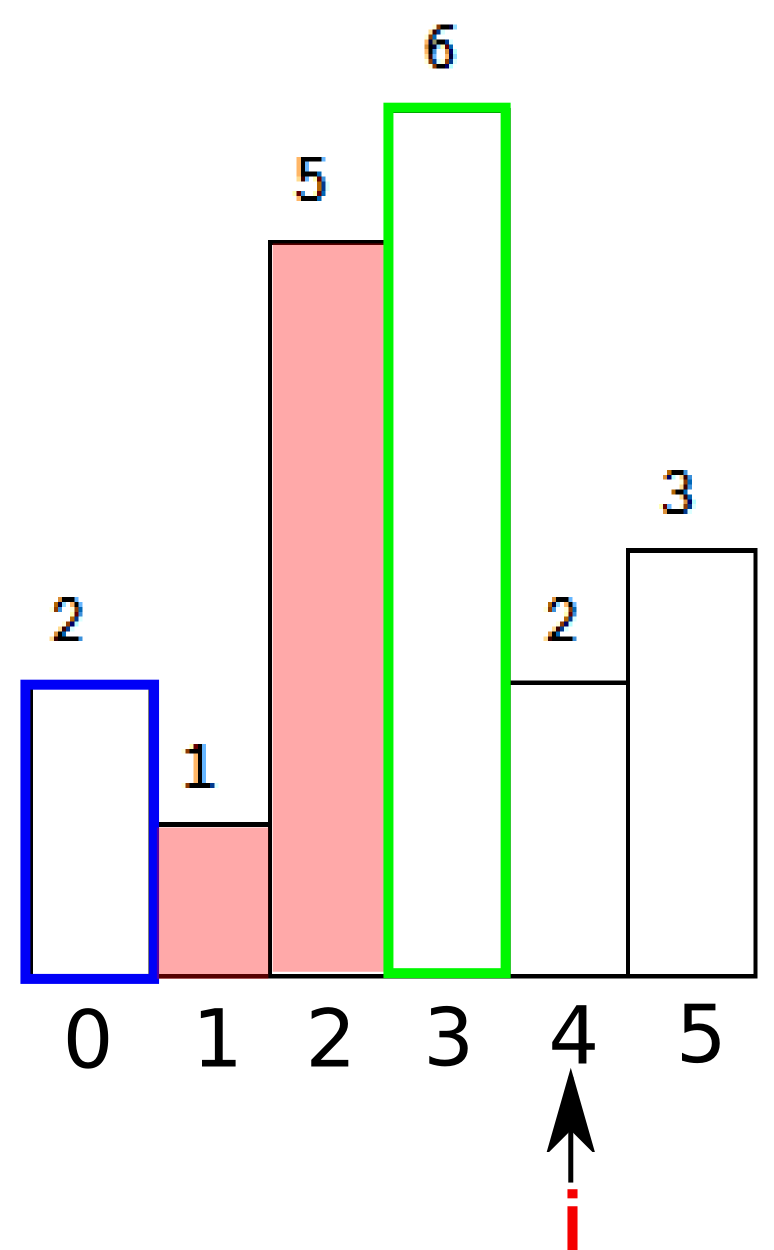
继续。这时候stack为空了,继续入栈。注意到只要是连续递增的序列,我们都要keep pushing,直到我们遇到了i=4,h[i]=2小于了栈顶的元素。
这时候开始计算矩形面积。首先弹出栈顶元素,t=3。即下图绿色部分。
接下来注意到栈顶的(索引指向的)元素还是大于当前i指向的元素,于是出栈,并继续计算面积,桃红色部分。
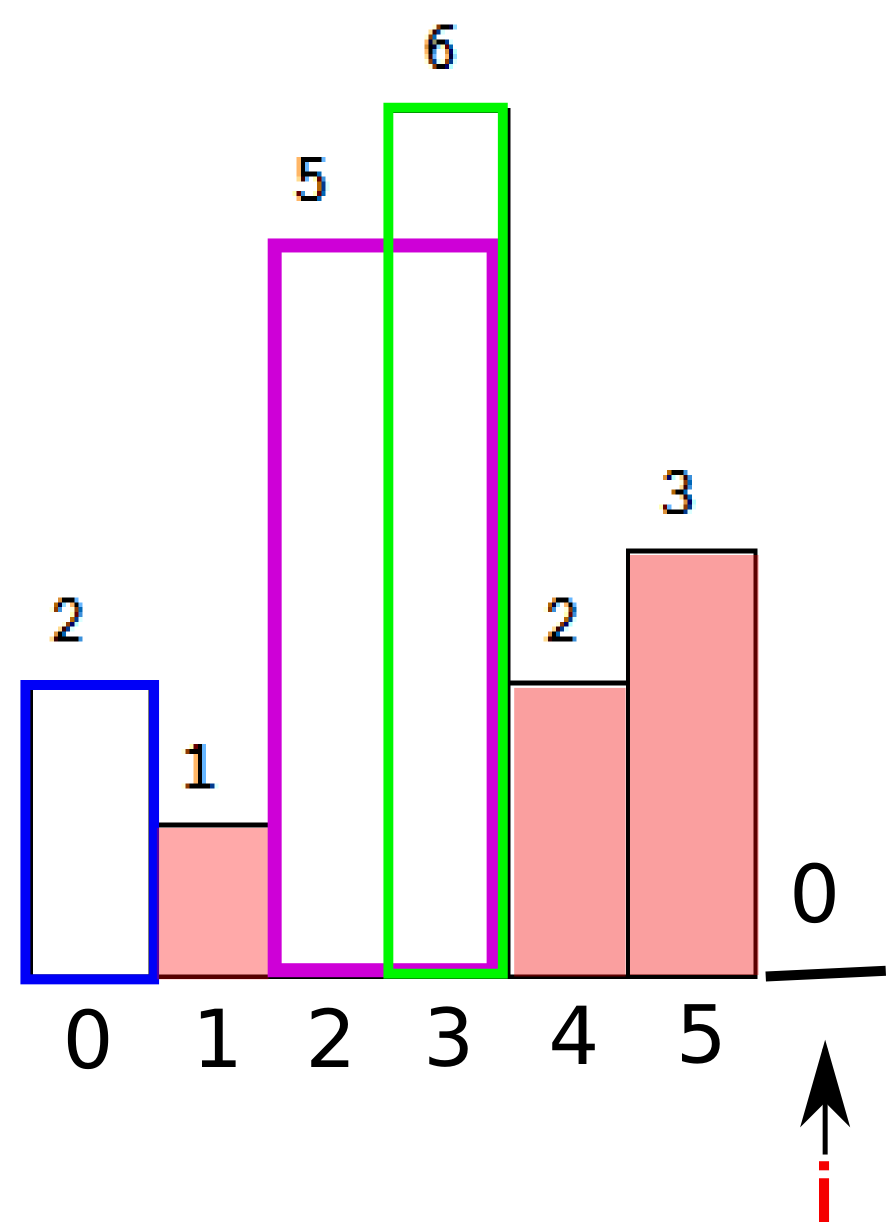
最后,栈顶的(索引指向的)元素大于了当前i指向的元素,循环继续,入栈并推动i前进。直到我们再次遇到下降的元素,也就是我们最后人为添加的dummy元素0.
同理,我们计算栈内的面积。由于当前i是最小元素,所以所有的栈内元素都要被弹出并参与面积计算。
注意我们在计算面积的时候已经更新过了maxArea。
解法:
#include
#include
#include
using namespace std;
int largestRectangleArea(vector& heights) {
int res = 0;
stack st;
heights.push_back(0);
for (int i = 0; i < heights.size(); ++i) {
while (!st.empty() && heights[st.top()] >= heights[i]) {
int cur = st.top(); st.pop();
res = max(res, heights[cur] * (st.empty() ? i : (i - st.top() - 1)));
}
st.push(i);
}
return res;
}
int main() {
vector vec{2,1,5,6,2,3};
int area = largestRectangleArea(vec);
cout << "Max Area: " << area << endl;
return 0;
} 其他题目
- 每日温度(单调栈)
- 下一个更大元素 II(单调栈)
- 最大矩形(单调栈)
- 接雨水(单调栈)
- 股票价格跨度(单调栈)
- 最大宽度坡(单调栈)