数据结构——顺序表和链表
目录
线性表
顺序表
顺序表的使用
结构体的定义
数据的初始化
数据容量的检查
头部插入数据
头部删除数据
尾部插入数据
尾部删除数据
任意数据删除
随机数据插入
数据查找
数据打印
数据修改
顺序表缺点
链表
结构体的创建
打印链表
新节点的建立
头部插入
尾部插入
头部节点删除
尾部节点删除
节点的销毁
链表查找
随即插入
后插
删除某节点前面的节点
删除某节点后面的节点
线性表
线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串...线性表在逻辑上是线性结构,也就说是连续的一条直线。但是在物理结构上并不一定是连续的,线性表在物理上存储时,通常以数组和链式结构的形式存储
链表
顺序表
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储。在数组上完成数据的增删查改。顺序表就是数组
2. 动态顺序表:使用动态开辟的数组存储。
typedef struct SeqList { SLDataType* array; // 指向动态开辟的数组 size_t size ; // 有效数据个数 size_t capicity ; // 容量空间的大小 }SeqList;
顺序表的使用
结构体的定义
typedef int SLDatatype;
typedef struct Sqelist
{
SLDatatype* a;//存储数据
int size;//当前存储个数
int capacity;//当前容量
}SL;数据的初始化
void SLInit(SL *psl)
{
assert(psl);
psl->a = NULL;
psl->capacity = psl->size = 0;
}数据容量的检查
void Checkcapacity(SL* psl)
{
if (psl->capacity == psl->size)
{
int newcapacity = psl->capacity == 0 ? 4 : psl->capacity * 2;
SLDatatype* tmp = (SLDatatype*)realloc(psl->a, sizeof(SLDatatype) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
psl->a = tmp;
psl->capacity = newcapacity;
}
}头部插入数据
void SLPpushfront(SL* psl, SLDatatype x)
{
assert(psl);
Checkcapacity(psl);
int end = psl->size - 1;
while (end >= 0)
{
psl->a[end + 1] = psl->a[end];
end--;
}
psl->a[0] = x;
psl->size++;
}头部删除数据
void SLPpopfront(SL* psl)//头删
{
assert(psl);
if (psl->size == 0)
return;
int i = 0;
for (i = 0; i < psl->size -1; i++)
{
psl->a[i] = psl->a[i + 1];
}
psl->size--;
}//这里不能进行所任,缩容是需要代价的,缩容分俩种,一种原地缩,第二种异地找个新空间大小为缩后的大小,若后期要插入元素,则又要开辟空间,比较麻烦尾部插入数据
void SLPpopback(SL* psl)
{
assert(psl);
if (psl->size == 0)
return;
psl->size--;
}尾部删除数据
void SLPpopback(SL* psl)
{
assert(psl);
if (psl->size == 0)
return;
psl->size--;
}任意数据删除
void SLErase(SL* psl, size_t pos)
{
assert(psl);
assert(pos < psl->size);
int i = 0;
for (i = pos; i < psl->size - 1; i++)
{
psl->a[i] = psl->a[i + 1];
}
psl->size--;
}随机数据插入
void SLInsert(SL* psl, int pos, SLDatatype x)
{
assert(psl);
assert(pos <= psl->size);
int i = 0;
Checkcapacity(psl);
for (i = psl->size; i >= pos; i--)
{
if (i == pos)
psl->a[i] = x;
else
psl->a[i] = psl->a[i - 1];
}
psl->size++;
}
/*size_t end=pls->size-1;
* while(end>=pos)
* {
* psl->a[end+1]=psl->a[end];
* --end;
* }
* psl->a[pos]=x;
* ++psl->size;
* 这种写法 pos会隐式提升为size_t(unsigned int)类型
* end 和 pos都为0之后,再--end,此时end变为一个非常大的数字
* 注意这里的隐式提升
* end和pos,俩个不能有一个是size_t类型,不然程序会出现错误
*/数据查找
int SLPfine(SL* psl, SLDatatype x)
{
assert(psl);
int i = 0;
for (i = 0; i < psl->size; i++)
{
if (psl->a[i] == x)
return i;
}
return -1;
}数据打印
void SLPprint(SL* psl)
{
assert(psl);
int i = 0;
for (i = 0; i < psl->size; i++)
{
printf("%d ", psl->a[i]);
}
}数据修改
void SLModify(SL* psl, size_t pos, SLDatatype x)
{
assert(psl);
assert(pos < psl->size);
psl->a[pos] = x;
}顺序表缺点
1. 中间/头部的插入删除,时间复杂度为O(N)
2. 增容需要申请新空间,拷贝数据,释放旧空间。会有不小的消耗。
3. 增容一般是呈2倍的增长,势必会有一定的空间浪费。例如当前容量为100,满了以后增容到 200,我们再继续插入了5个数据,后面没有数据插入了,那么就浪费了95个数据空间。
链表
链表:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表 中的指针链接次序实现的 。 单链表不需要初始化
结构体的创建
正确写法
typedef int SLTDataType; typedef struct SlistNode { SLTDataType data; struct SlistNode* next; }SLTNode;错误写法
typedef struct SlistNode { SLTDataType data; struct SlistNode* next; //SLTNode*next; 错误写法,先有蛋还是先有鸡? // SlistNode* next; 错误写法, }SLTNode;typedef struct SlistNode { SLTDataType data; struct SlistNode* next; }SLTNode,*PSLNode;SLTNode*= PSLNode= struct SlistNode*,这三个等价
打印链表
void SListprint(SLTNode* phead) { //phead可能会为空这里不需要断言 SLTNode* cur = phead; while (cur != NULL) { printf("%d->", cur->data); cur = cur->next; } }
新节点的建立
SLTNode* BuySLTnode(SLTDataType x) { SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode)); if (newnode == NULL) { perror("malloc fail"); exit(-1); } newnode->data = x; newnode->next = NULL; return newnode; }需要新节点的地方会很多,建立一个新的函数专门建立节点
头部插入
创建新节点前,phead指向第一个节点
创建新节点:先让newnode->next指向phead, phead指向第一个节点的地址,也就是说新节点通过phead拿到了原来第一个节点的地址
然后让phead指向新节点地址
void SListpushfront(SLTNode* phead, SLTDataType x) { SLTNode newnode;//错误写法 SLTNode* newnode =(SLTNode*) malloc(sizeof(SLTNode)); }上面为错误代码不能用是因为:不能用局部节点,不然一出该函数就会被销毁,因此我们要用上面的函数来创建节点
方式1:
void SListpushfront(SLTNode* phead, SLTDataType x) { SLTNode* newnode = BuySLTnode(x); newnode->next = phead; phead = newnode; }运行后无法打印,这是因为我们在传参的时候没有传地址 ,因此在出建立节点的函数的时候会对形参销毁
方式二,传地址
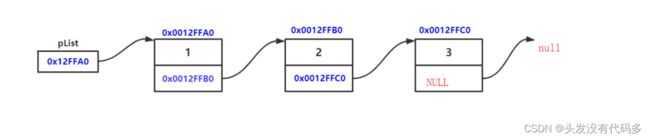
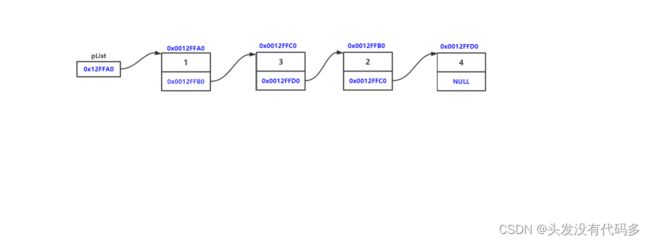
SLTNode* plist=NULL; SListpushfront(&plist, 5); void SListpushfront(SLTNode**pphead, SLTDataType x) { SLTNode* newnode = BuySLTnode(x); newnode->next =*pphead; *pphead = newnode; }pphea存的是plist的地址,*pphead的plist=等号右边的值,可参考下图,此时能正常打印。
尾部插入
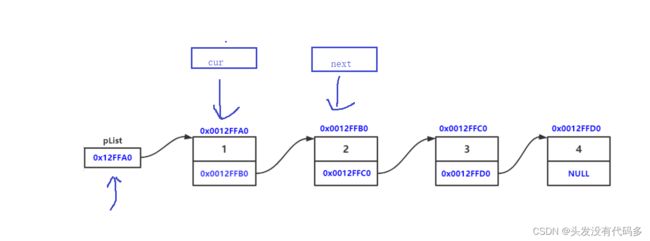
先建立一个新的节点
分为俩种情况,第一种头节点指向空,第二种头节点指向不为空
第一种情况:头节点为空,建立新的节点后,直接让头节点指向新节点
第二种情况,头节点不为空,创建一个跟节点类型相同的结构体变量,然后让这个变量指向头节点,之后检查后面的每个节点,若有一个节点为的next为空,则在此处插入新节点
tail发现这个节点的next指向为空,然后让这个节点的next指向下一个节点的地址,随着程序的结束tail也会随之消失
void SListpushback(SLTNode** pphead, SLTDataType x) { //pphead不可能为空,pphead是plist的地址,pphead永远不为空 //1.链表为空 SLTNode* newnode = BuySLTnode(x); if (*pphead == NULL) { *pphead = newnode; } //2.不为空 else { SLTNode* tail = *pphead; while (tail->next != NULL) { tail =tail->next; } tail->next = newnode; } }频繁的malloc会使效率降低
头部节点删除
void SListpopfront(SLTNode** pphead)//头删 { SLTNode* del = *pphead; *pphead = (*pphead)->next; free(del);//删除第一个节点 del = NULL; }当全部删完后,plist指向NULL,此时就不能再删了。程序会崩溃,此时plsit为空,(*pphead)->next也为空,del也为空,因此加一个检查条件
void SListpopfront(SLTNode** pphead)//头删 { if(*pphead==NULL) { return; } SLTNode* del = *pphead; *pphead = (*pphead)->next; free(del);//删除第一个节点 del = NULL; }或
void SListpopfront(SLTNode** pphead)//头删 { assert(*pphead!=NULL); SLTNode* del = *pphead; *pphead = (*pphead)->next; free(del);//删除第一个节点 del = NULL; }
尾部节点删除
当tail->next为空,删除该节点,然后让前一个节点指向NULL
void SListpopback(SLTNode** pphead) { if(*pphead==NULL) return; if((*pphead)->next==NULL) { free(*pphead); *pphead=NULL; } else { SLTNode* prev = NULL; SLTNode* tail = *pphead; while (tail->next!= NULL) { prev = tail; tail = tail->next; } prev->next = NULL; free(tail); tail = NULL; } }或
void SListpopback(SLTNode** pphead) { if(*pphead==NULL) return; if((*pphead)->next==NULL) { free(*pphead); *pphead=NULL; } else { SLTNode* tail = *pphead; while (tail->next->next!= NULL) { tail = tail->next; } free(tail->next); tail->next = NULL; } }
节点的销毁
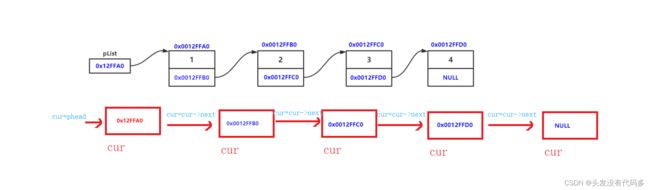
释放掉cur,cur=next ,不断往下走,最后把头节点置空
void SListDestory(SLTNode** pphead)//用二级指针会更好 { SLTNode* cur = *pphead; while (cur) { SLTNode* next = cur->next; free(cur); cur = next; } *pphead = NULL; }
链表查找
SLTNode *SListFind(SLTNode** pphead, SLTDataType x) { SLTNode* cur = *pphead; while (cur != NULL) { if (cur->data == x) { return cur; } cur = cur->next; } return NULL; }挨个查找。
随即插入
void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x) { assert(pos); if (pos == *pphead) { SListpushfront(pphead, x); } else { SLTNode* prve = *pphead; while (prve->next != pos) { prve = prve->next; assert(prve);//找不到 } SLTNode* newnode = BuySLTnode(x); prve->next = newnode; newnode->next = pos; } }从一个数的前面插入,若果头插则用头插函数
后插
void SListInsertAfter(SLTNode** pphead, SLTNode* pos, SLTDataType x) { SLTNode* newnode = BuySLTnode(x); newnode->next = pos->next; pos->next = newnode; }
删除某节点前面的节点
void SlistErase(SLTNode** pphead, SLTNode* pos) { assert(pos); if (*pphead == pos) { SListpopfront(pphead); }//如果是头删,用头删函数 else { SLTNode* prev = *pphead; if (prev->next != pos) { prev = prev->next; assert(prev);//判断pos是否属于本链表 } prev->next = pos->next; free(pos); pos = NULL; } }
删除某节点后面的节点
void SlistEraseAfter(SLTNode** pphead, SLTNode* pos) { assert(pos); if (pos->next == NULL) return; else { SLTNode* prev = *pphead; prev = pos->next; pos->next = prev->next; free(prev); prev = NULL; } }
单链表缺陷
单链表只适合头插头删,O(1)。
替换法删除节点
删除某个节点,要求是O(1)
把2所在节点删除,可采用以下方法, 我们把2,3进行交换
然后让3指向4
缺陷:所删节点不能是尾节点,尾节点后面是空的,无法交换
思路延申
在pos之前插入,要求是O(1)
我们不在之前插入,在之后进行插入
然后交换值