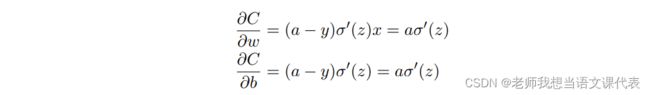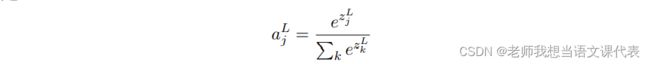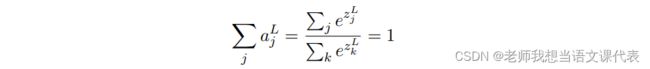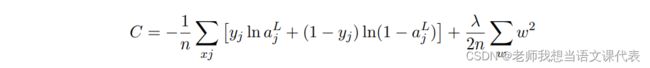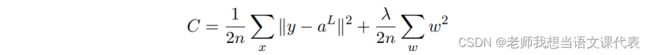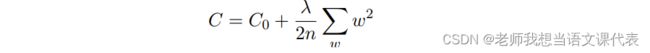Neural Network and Deep Learning-学习笔记2-改进神经网络的学习方法
1. 交叉熵代价函数
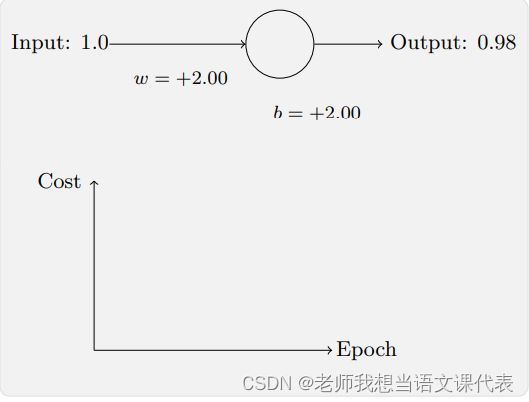
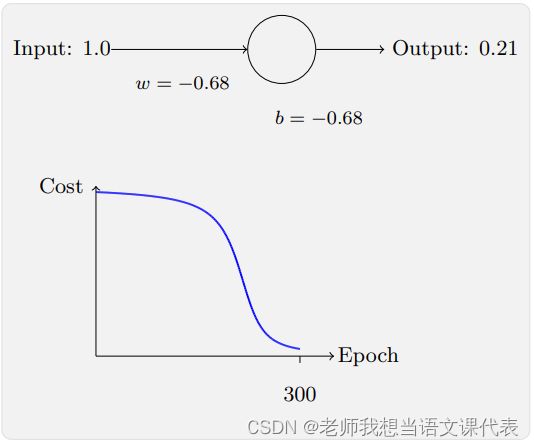
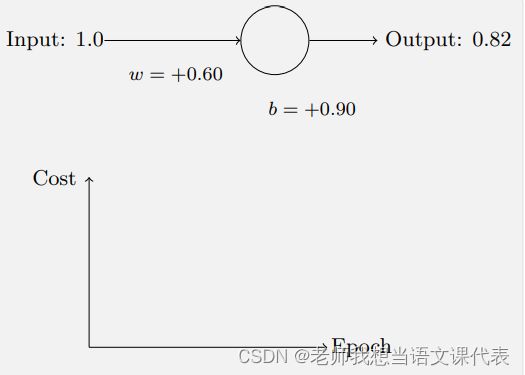
下面这个例子我们可以看到刚开始的学习速度是⽐较缓慢的。对前 150 左右的学习次数,权重和偏置并没有发⽣太⼤的变化。随后学习速度加快,神经⽹络的输出也迅速接近 0.0。
为了理解这个问题的源头,想想我们的神经元是通过改变权重和偏置,并以⼀个代价函数的 偏导数(∂C/∂w 和 ∂C/∂b)决定的速度学习。所以,我们在说“学习缓慢”时,实际上就是说 这些偏导数很⼩。我们⼀直在⽤的是⽅程 ![]() 表⽰⼆次代价函数,其中 a 是神经元的输出,训练输⼊为 x,输出为y。显式地使⽤权重和偏置来表达这个,我们有 a = σ(z),其中 z = wx + b。使⽤链式法则来求权重和偏置的偏导数:
表⽰⼆次代价函数,其中 a 是神经元的输出,训练输⼊为 x,输出为y。显式地使⽤权重和偏置来表达这个,我们有 a = σ(z),其中 z = wx + b。使⽤链式法则来求权重和偏置的偏导数:
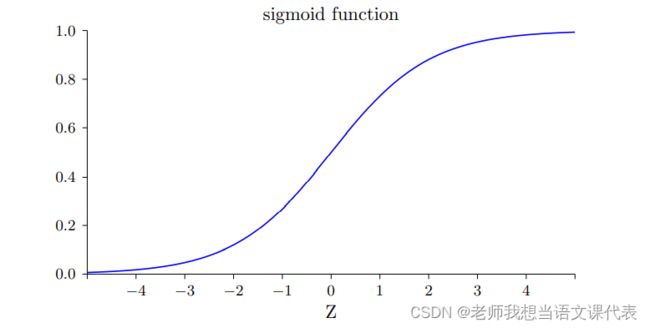
让我们仔细看 σ ′ (z) 这 ⼀项。⾸先回忆⼀下 σ 函数图像:
我们可以从这幅图看出,当神经元的输出接近 1 的时候,曲线变得相当平,所以 σ ′ (z) 就很 ⼩了。上述方程也告诉我们 ∂C/∂w 和 ∂C/∂b 会⾮常⼩。这其实就是学习缓慢的原因所在。我们后⾯也会提到,这种学习速度下降的原因实际上也是更加⼀般的神经⽹络学习缓慢的原因,并不仅仅是在这个特例中特有的。
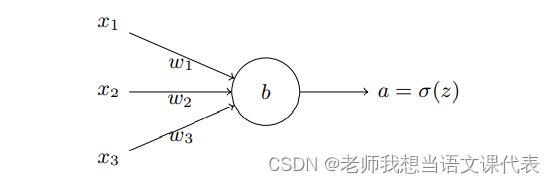
那么我们如何解决这个问题呢?研究表明,我们可以通过使⽤交叉熵代价函数来替换⼆次代价函数。我们现在要训练 ⼀个包含若⼲输⼊变量的的神经元,x1, x2, . . . 对应的权重为 w1, w2, . . . 和偏置 b:
神经元的输出就是 a = σ(z),其中 z = ∑ wjxj + b 是输⼊的带权和。我们如下定义这个神 经元的交叉熵代价函数:
![]()
其中 n 是训练数据的总数,求和是在所有的训练输⼊ x 上进⾏的,y 是对应的⽬标输出。算交叉熵函数关于权重和偏置的偏导数:
![]()
![]()
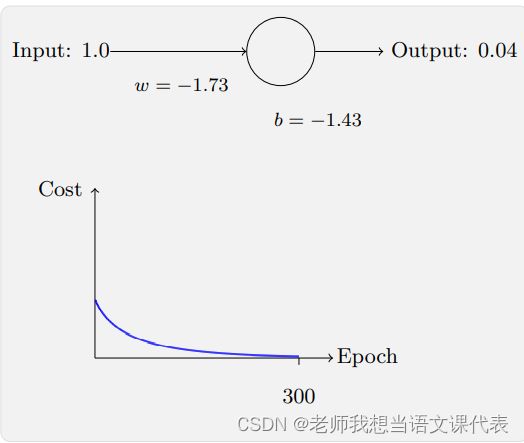
它告诉我们权重学习的速度受到 σ(z) − y,也就是输出中的误差的控制。这个代价函数还避免了⼆次代价函数中类似⽅程中 σ ′ (z) 导致的学习缓慢,当我们使⽤交叉熵的时 候,σ ′ (z) 被约掉了,所以我们不再需要关⼼它是不是变得很⼩。让我们重回最原初的例⼦,来看看换成了交叉熵之后的学习过程。现在仍然按照前⾯的参数 配置来初始化⽹络,开始权重为 0.6,⽽偏置为 0.9,看看在换成交叉熵之后⽹络的学习情况,你将看到如下变化的曲线:
这次神经元的学习速度相当快,代价函数曲线要⽐⼆次代价函数训练前⾯部分要陡很多。说明当神经元开始出现严重错误时能以最快速度学习。
这个例⼦中η = 0.005,使⽤⼆次代价函数的时候,η = 0.15,这些现象并不依赖于如何设置学习速率。一般输出神经元是 S 型神经元时,选交叉熵代价函数;输出神经元是线性的,选二次代价函数。
柔性最大值阈值函数*
⼤多数情况使⽤交叉熵来解决学习缓慢的问题。现在简要介绍⼀下另⼀种解决这个问题的⽅法,基于柔性最⼤值(softmax)神经元层。
柔性最⼤值的想法其实就是为神经⽹络定义⼀种新式的输出层。开始时和 S 型层⼀样的,⾸先计算带权输⼊![]() 。在这一层上将S 型函数全部替换为⼀种叫做柔性最⼤值函数,应用在
。在这一层上将S 型函数全部替换为⼀种叫做柔性最⼤值函数,应用在![]() 上,根据这个函数,第j个神经元的激活值
上,根据这个函数,第j个神经元的激活值![]() 就是:
就是:
其中,分⺟中的求和是在所有的输出神经元上进⾏的。根据定义,输出的激活值加起来正好为 1:
柔性最⼤值层的输出可以被看做是⼀个概率分布。
2. 过拟合与规范化
过拟合
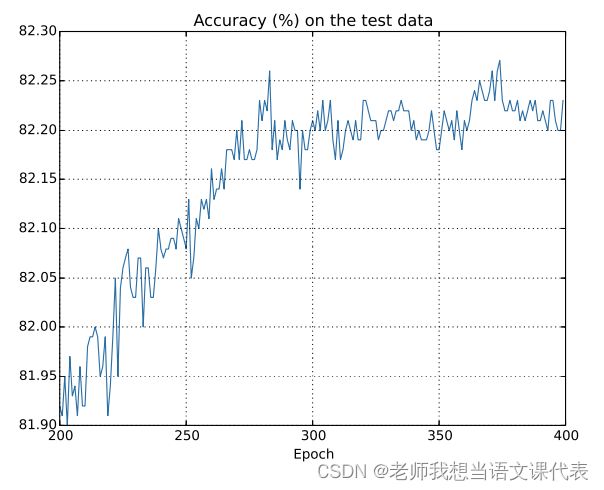
在前 200 迭代期(图中没有显⽰)中准确率提升到了 82%。 然后学习逐渐变缓。最终,在 280 迭代期左右分类准确率就停⽌了增⻓。们的⽹络在 280 迭代期后就不在能够推⼴到测试数据上。所以这不是有⽤的学习。我们说⽹络在 280 迭代期后就过度拟合(overfitting)或者过度训练(overtraining)了。
规范化(正则化)
规范化是用来缓解过拟合的技术,现给出⼀种最为常⽤的规范化⼿段 —— 有时候被称为权重衰减(weight decay)或者 L2 规范化。L2 规范化的想法是增加⼀个额外的项到代价函数上, 这个项叫做规范化项。下⾯是规范化的交叉熵:
其中 λ > 0 可以称为规范化参数,n 是训练集合的⼤⼩。我们会在后⾯讨论 λ 的选择策略。需要注意的是,规范化项⾥⾯并不包含偏置。这点我们后⾯也会在讲述。对其他的代价函数也可以进⾏规范化,例如⼆次代价函数:
两者都可以写成这样:
其中 C0 是原始的代价函数。
直觉地看,规范化的效果是让⽹络倾向于学习⼩⼀点的权重,其他的东西都⼀样的。规范化可以当做⼀种寻找⼩的权重和最⼩化原始的代价函数之间的折中。这两部分之前相对的重要性就由 λ 的值来控制了: λ 越⼩,就偏向于最⼩化原始代价函数,反之,倾向于⼩的权重。对上述方程求偏导数得:
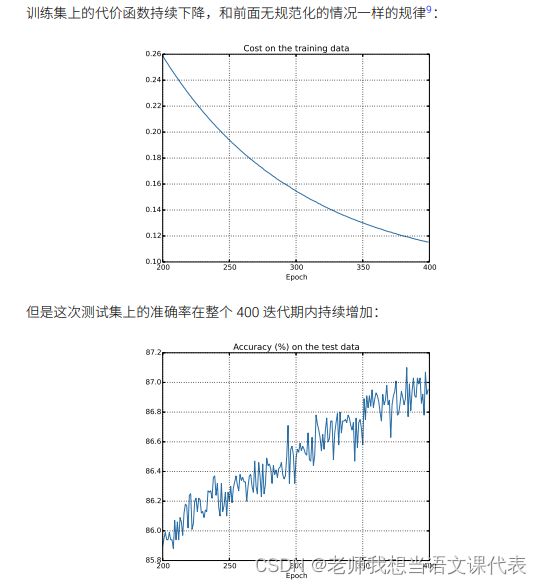
这种调整有时被称为权重衰减。实验效果好:
其他规范化技术:
L1 规范化: 这个⽅法是在未规范化的代价函数上加上⼀个权重绝对值的和:
![]()
弃权: 弃权(Dropout)是⼀种相当激进的技术。和 L1、L2 规范化不同,弃权技术并不依赖对代价函数的修改。⽽是改变了⽹络本⾝。
⼈为扩展训练数据