堆与堆排序
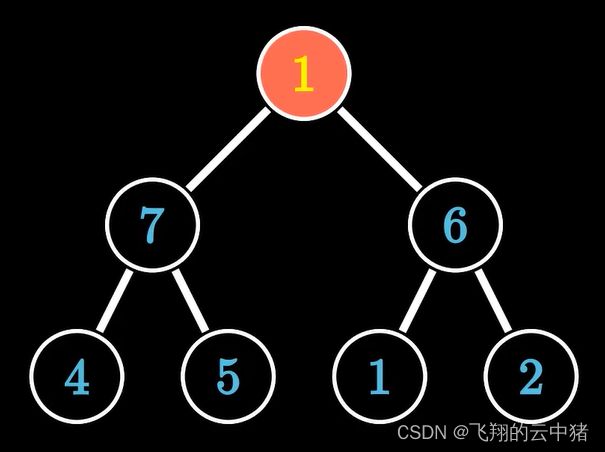
一.什么是堆?
大根堆每个结点都大于等于它的两个子结点,这里要注意堆中仅仅规定了每个结点大于等于它的两个子结点,但这两个子结点的顺序并没有做规定,跟二叉查找树是有区别的。
小根堆则是小于等于它的两个子结点。
二.堆的实现
堆通常用数组来实现
具体方法就是讲二叉树的结点按照层级顺序放入数组中,根结点在位置1,它的子节点在位置2和3,而子节点的子节点则分别在位置4,5,6,7,以此类推。
上面这张图是从1开始的,但是我习惯从0开始(因为数组的索引一般是从0开始)。
这样的话如果一个父结点的下标为i,则它的父结点的位置为i/2,而它的2i+1和2i+2。这样,在不适用指针的情况下,我们也可以通过计算数组的索引在堆中上下移动。
三.堆的基本操作【上滤,下滤,建堆】
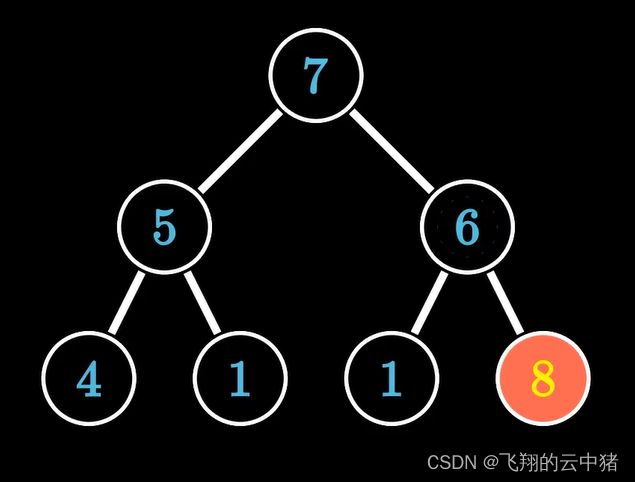
1.下滤
只有树的根元素破坏了堆序性。
我们将破坏堆序性的元素与他的最大子结点比较,如果小于他的最大子结点,如果小于他的最大子结点,则与之交换,持续比较交换,直到该元素大于他的子节点为止,或者移动到底部为止,此时该树就成功地被调整成一个大根堆。我们把根结点向下调整的操作称为下滤,很容易看出复杂度为logN。
2.上滤
只有树的最后一个元素破坏了堆序性。
同理让它和它的父元素比较,若大于父节点则交换,直到无法上移为止。
这个操作主要用于插入新元素到堆中。复杂度也为logN。
3.建堆
如果有一个乱序的数组,怎么操作让它整理为堆呢?
有两种方法,一种方法为自顶向下建堆法,对应的操作为上滤。
【1】自顶向下建堆法
方法:插入堆->上滤
【2】自下向上建堆法
方法:对每个父结点进行下滤
四.堆排序及实现步骤
1. 构造堆(如果要从小到大则构造大顶堆,否则小顶堆)
2.得到堆顶元素,这个值就是最大值
3.交换堆顶元素和数组中的最后一个元素,此时所有元素中的最大元素已经放到了合适的位置
4.对堆顶的元素进行上滤操作,重新让除了最后一个元素的剩余元素中的最大值放到堆顶。
5.重复2-4步骤,直到堆中剩一个元素为止。
示例代码:将一个数组从小到大排序:
#include
using namespace std;
// 调整大顶堆的函数
void heapify(int arr[], int n, int i) {
int largest = i; // 初始化最大元素为根节点
int left = 2 * i + 1;
int right = 2 * i + 2;
// 如果左子节点比根节点大,则更新最大元素的索引
if (left < n && arr[left] > arr[largest])
largest = left;
// 如果右子节点比当前最大元素大,则更新最大元素的索引
if (right < n && arr[right] > arr[largest])
largest = right;
// 如果最大元素不是根节点,则交换根节点和最大元素的位置
if (largest != i) {
swap(arr[i], arr[largest]);
// 继续调整以确保新的子树也满足大顶堆的性质
heapify(arr, n, largest);
}
}
// 堆排序函数
void heapSort(int arr[], int n) {
// 构建初始的大顶堆,从最后一个非叶子节点开始
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 依次将堆顶元素(最大值)与数组末尾元素交换,并重新调整堆
for (int i = n - 1; i > 0; i--) {
swap(arr[0], arr[i]); // 将当前最大值放到数组末尾
heapify(arr, i, 0); // 重新调整堆,排除已排序的部分
}
}
// 输出数组元素的辅助函数
void printArray(int arr[], int n) {
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << endl;
}
// 测试堆排序算法
int main() {
int arr[] = {9, 3, 7, 5, 1, 6, 8, 2, 4};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "原始数组:" << endl;
printArray(arr, n);
heapSort(arr, n);
cout << "排序后的数组:" << endl;
printArray(arr, n);
return 0;
}
如果从大到小排序,只要将构造大顶堆的函数改为构造小顶堆即可:
// 调整小顶堆的函数
void heapify(int arr[], int n, int i) {
int smallest = i; // 初始化最小元素为根节点
int left = 2 * i + 1;
int right = 2 * i + 2;
// 如果左子节点比根节点小,则更新最小元素的索引
if (left < n && arr[left] < arr[smallest])
smallest = left;
// 如果右子节点比当前最小元素小,则更新最小元素的索引
if (right < n && arr[right] < arr[smallest])
smallest = right;
// 如果最小元素不是根节点,则交换根节点和最小元素的位置
if (smallest != i) {
swap(arr[i], arr[smallest]);
// 继续调整以确保新的子树也满足小顶堆的性质
heapify(arr, n, smallest);
}
}