CSP-S 2020考前冲刺笔记
文章目录
- 停课前
-
-
- 2020.10.14
- 2020.10.15
- 2020.10.16
- 2020.10.17
- 2020.10.18
-
- 停课后
-
-
- 2020.10.19
- 2020.10.20
- 2020.10.21
-
停课前
2020.10.14
P1082: 学习了扩欧,板子题
P3811: 学习了线性求逆元,板子题
ACL B: 枚举 k k k与 k + 1 k+1 k+1分别能被哪两个积为 n n n的数整除,然后跑几遍扩欧并取最小值即珂。
2020.10.15
P3811: 学习了积性函数线性筛,换了一种方式A掉
P3455: 莫反板子题,用线性筛求了下莫比乌斯函数
CF1187E: 又水又裸的换根 d p dp dp,切掉
2020.10.16
P5676: 数学与图论建模题,它对它的倍数连边,一个 w i w_i wi与 e i e_i ei连边;然后直接缩点,对于每一个大小不小于 2 2 2的联通块内每个节点都珂以重复经过。根据任何数都珂以分解成若干个质数的乘积,我们珂以优化建图。
CF1423K: 找规律题,答案为 ( n , n ] (\sqrt n, n] (n,n]中质数的个数 + 1 +1 +1。
P6812: 先挖一个性质,然后线段树维护即可。
一定要注意下传标记时的 f f f函数要打上标记
2020.10.17
P5022: 树的情况就是很水的贪心,对于基环树我们 O ( n ) O(n) O(n)枚举删边,然后使用按秩合并并查集判环之后与树的情况类似地跑一遍来更新答案。大力卡常也过不了
判是否存在环一定要用并查集,别自以为是地乱搞
P1350: 枚举在右下角的子矩阵中车的数量,然后用逆元求组合数推一下式子就完了。
P5021: 先二分,然后贪心乱搞;看到达到 m i d mid mid的链就砍一刀;否则先排序这些伸出的链的长度,接着双指针搞一搞就完了。可是不知道为什么最后 4 4 4个点一直WA
2020五校联考:
T1: 容易发现所有概率的平均值就是一次产生伤害的概率,就转换成了 n = 1 n=1 n=1的情况;然后推一推式子就能求出产生 K K K点伤害的概率,接着反面考虑用前缀和优化一下就完了……注意使用Lucas定理搞组合数,蓝。
T2: 对于每一个区间,我们从小到大去膜;然后再推一推式子,根据前缀和提出来,最后用标记永久化线段树优化一下就完了,紫。
T3: 维护一下看到当前各个数是否出现的一个数组,如果以 a i a_i ai为中心不是一个回文串就可以;然后哈希一下,由于它是动态的就上线段树来维护一波,蓝。
T4: 大力排序,分段 d p dp dp;每次根据四种走法取最小值转移即可,蓝。
T5: 二分走的路程,然后大力分类讨论线性 d p dp dp就做完了,蓝。
2020.10.18
P3805: 学习了神奇的 O ( n ) O(n) O(n)马拉车算法,自己想出了二分套哈希的 O ( n l o g n ) O(nlogn) O(nlogn)写法。
P3386: 复习了匈牙利算法,简洁了自己的代码,并且还写挂了多次,起到了很好的巩固作用。
CF620E: 本来想用线段树套数组写法,发现会MLE;于是就通过标签学会了线段树套状压的写法。时间复杂度不变,空间复杂度大幅下降。一直WA也不知道怎么回事
注意: pushdown后一定要清楚标记!
CF1387B1: 比较裸的贪心,切掉
P6722: 找到直径的中点,看看它到直径两端的距离是否都达到了 k k k即可。
注意: 由于有负边,强制用 d p dp dp求树的直径.
[RC-03]难题: 比较水的贪心。显然,对应位不同是最佳选择。所以,我们令 a = n a=n a=n, b b b为 a a a的有效位取反的值。
[RC-03]随机树生成器: 根据期望推式子,然后线性求逆元,用前缀和维护一下就做完了。
洛谷10月月赛II:
T1: 结论题,如果 n n n为奇数每条边都能走,否则不能走 n 2 − 1 \frac n 2-1 2n−1条边,减去即可。橙。
T2: 用部分分来搞正解:
①观察规律,如果 m = 0 m=0 m=0,那么答案就是 ∑ i = 1 n i + n \sum_{i=1}^n i+n ∑i=1ni+n。
②乱搞得规律,如果 m = 1 m=1 m=1,可以说成是由 n + 1 , 0 n+1,0 n+1,0通过一步操作转化而来的;所以 n , 1 n,1 n,1的答案就是 n + 1 , 0 n+1,0 n+1,0的的答案。
③提炼总结。假设没有 m = 0 m=0 m=0或 m = 1 m=1 m=1的约束条件,可以发现——如果对 n n n个带圣盾的胖头鱼进行操作,就变成了 m = 1 m=1 m=1的情况;否则,我们 m m m就减去了 1 1 1,继续递归下去; m = 1 m=1 m=1为边界。
注意逆元即可。
T3: 看到题目,以为是动态 d p dp dp? 立即否认了……于是开始打 20 20 20分的小优化暴力,拿到 20 20 20分后尝试了线段树,发现思路错误。
T4: 看到题目,先通过暴力程序找出了性质,然后用莫比乌斯反演推了推式子……注意线性筛莫比乌斯函数,拿到了不错的 50 50 50分。
回去想 T 3 T3 T3,想了半个小时也毫无思路……于是就 270 270 270滚粗……
后来听了 b ruteforce \color {black} \text {b} \color {red} \text {ruteforce} bruteforce巨佬讲课,发现 T 2 T2 T2如此得简单,为啥要想 1.5 h 1.5h 1.5h……而 T 3 T3 T3是一个有套路性地解法,然后数据结构上二分就做完了。
T4是一个欧拉函数的杜教筛?但似乎莫反加上杜教筛也能过?反正严重超纲,这题听了几个字就咕了。
CF1045I: 哈希水题,切掉
停课后
2020.10.19
一回家,我妈就给我打电话,说可以查到分数了……就要了个链接,怀着忐忑的心一查……毫无悬念地过了。
然后就很开心,跟老师(OI&&whk)打了个电话,说了说停课的事情;接着就开始准备复赛。
CF1426: 贪心想了想,怕有反例;就打了个暴力 O ( 9 ! × 9 ) O(9!×9) O(9!×9)的,轻松通过;写了个题解。
CF638C: 树上贪心水题,切掉,写了个题解。
P2512: 听说这题是《算法竞赛进阶指南》上原题,但是上一次看到这例题还是半年前……还能不忘吗……于是就不会做了,然后复习了一下,恍然大悟。顺便又切了一次均分纸牌,我不会告诉你第一次我做均分纸牌因看错题目而WA了两位数次
突然想起来还有一场ABC没看,于是就去看了……
ABC 180 E: 裸的状压,代码不写了QAQ
ABC 180 F: 挖了三个性质,感觉会做,没有想得很透彻……就走人了(搬家)
CF 1045 I突然发现UKE了?编译失败了?原来是Codeforces变成Queueforces了……重交一遍就A了,差点又一次在不知不觉中做错了一道代码正确的题
2020.10.20
LOJ #10001: 我竟然不会做……比较水的贪心题,按右端点排序,如果右端点相同按左端点排序。每次尽可能地在尾部种树;当然,例如在这个区间内一共要种 5 5 5棵树,之前已经决定种了 3 3 3棵树,那么在 r − 1 , r r-1,r r−1,r各种一棵树就好了。时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。
LOJ #10002: 计算几何题……首先,我们用勾股定理找出这个圆对应的区间,按右端点排序,然后直接贪心地扫一遍就做完了。可是只有 83 83 83分,也不知道为什么,我太菜了……
LOJ #10003: 使用微扰(临项交换)推式子,可以找到贪心策略,然后直接用Johnson算法排序;最后模拟一遍就行了。
LOJ #10009: 比较水的三维 d p dp dp,不优化就能过。
LOJ #10008: 贪心,用堆维护最优决策即可。
回洛谷……
CF1045I发现UKE了?重交就AC了……惨,差点又做错了一道代码正确的题……
P1196: 由于我还对并查集不是很熟悉,就做了一道并查集的题目,题目没看完就开了题解……就是一个边带权的并查集,也没啥特别的。
P2024: 扩展域并查集的板子,发现扩展域忘了之后仍然是题目没看完就开了题解……
去CF……
由于今天晚上我要用小号打一场Div.3,所以就打了一场Div.3的虚拟赛……结果前五题不到 40 40 40分钟就切完了,然后装修,就跑到广场上去做题…… F F F的式子推出来了,就不打代码了,我真的跟鸽子差不多呢
CF620E: 之前WA了,现在改了一点,结果T了?发现自己写了个假复杂度的标记下传,改了一改,又大力卡常,各种神奇的方式都用上了……最终好不容易通过了这题。但似乎大家都没有被这题卡常,而是 1 1 1秒钟相处思路, 1 1 1分钟切掉……我怎么这么菜啊……
然后就开始看《算法竞赛进阶导论》。休息一会儿,不要马上比赛打一半睡着了QAQ
然后 D i v . 3 Div.3 Div.3死在了调试能力上,都是"一眼出思路,一秒写代码,一天调不出"这种情况……最终惨死在了第 200 200 200多名……要是再被 H a c k Hack Hack一下我就真的自闭了……
2020.10.21
做了个决定,从这天下午开始,所有题目上难度。
P3375; 学会了KMP,感谢姐姐"皎月版洒花";
LOJ #10015: 直接二分一个时刻,然后 O ( n 2 ) O(n^2) O(n2)枚举用并查集维护,最后判断一下是否为联通图即珂。
CF1355E: 之前给@b6e0巨佬切掉的一个三分题,然后我看到这题,就果断选择了枚举最后变成的那个数;发现这样会超时,于是就上了三分就过了。第一次使用三分套贪心,感觉不错!
把昨天Div.3的G题的代码补了一下,为了锻炼代码能力,逼自己 10 10 10分钟内打完代码,调试完毕,提交并 A C AC AC,最终竟然成功了?看来逼一逼自己还是有用的……
从此,我只刷蓝紫黑题了。
CF734E: 没做出来QAQ——我们先对相同颜色的联通块,用并查集来进行缩点,然后此时的新树两个被一条边连的节点颜色不同,就可以跑出直径,答案就是直径长度除以 2 2 2向上取整,即从直径中点向两边’扩散"最优。时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。我太菜了……
CF466E: 没做出来QAQ——我们离线搞,通过并查集建树,然后离线下来预处理,之后我们每次只需要查询是否在链上即珂,通过"求距离"珂以做到,而"求距离"又珂以通过LCA来做到。写了个LCA的板子,没写挂感觉不错。我太菜了……
CF960E: 贡献题,感觉比较水,结果切掉了……爽。
然后又把KMP板子打了一遍。
之后做的题目越来越难,所以下面的就是每日的刷题笔记。
10.22: 效率极高的一天的刷题笔记
有几天的效率还不错,也有几天的效率并不高。
距离比赛只有 10 10 10天了……
2020.10.28
P5588: 大力分讨题。
①如果不存在这种颜色,直接输出 n ( n − 1 ) 2 \frac {n(n-1)} 2 2n(n−1)
②如果这种颜色只出现了一次,就保存下与这个节点相连的各个节点的 s i z e size size,然后求 ∑ i = 1 k ∑ j = 1 i − 1 s i z e i s i z e j \sum_{i=1}^k \sum_{j=1}^{i-1} size_i\ size_j ∑i=1k∑j=1i−1sizei sizej珂以通过处理前缀和来快速查询.
③如果这种颜色出现的次数大于 1 1 1次,首先通过相反的两遍 d f s dfs dfs来判断这些节点是否在一条链上并能找到这条链的两个端点 u , v u,v u,v。如果这两个端点在一条链上,就倍增找祖先乱搞;否则就是 s i z e u s i z e v size_u size_v sizeusizev。
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn),开了不下 20 20 20个数组(包括 s t r u c t struct struct与 v e c t o r vector vector等STL容器),结果凭借超强的码力 5 5 5分钟打完代码AC,爽!
P2746: 缩点+性质题。
首先,缩点是必须要缩的;不然一个连通块你到不了别的连通块,但是因为这个连通块本身而认为珂以到得了,这是什么逻辑。
①缩点
②考虑两个答案。由于缩点后是一个DAG,所以第一个答案就是入度为 0 0 0的点的数量;第二个答案就是入度为 0 0 0的点的数量与 1 1 1的点的数量的较大者。
结果QAQ:
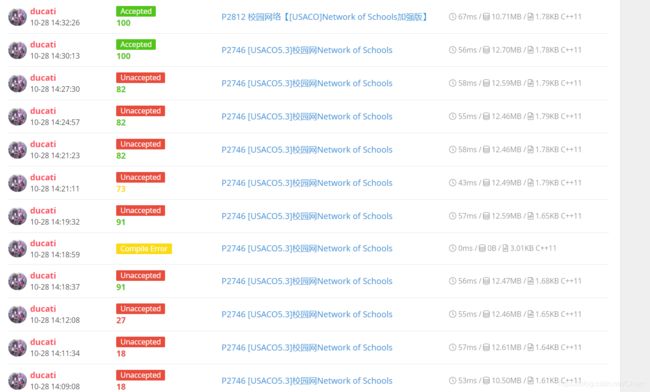
惨……
我去多校玩啦
犯了各种sb错误,要是在CSP上考了这题就凉凉了。
HDU1598: 这么裸的图论并查集我这个菜鸡竟然没做出来……
对于每次询问,我们枚举 l , r l,r l,r,作为所选路径的边权的最小值与最大值,然后加上所有在 [ l , r ] [l,r] [l,r]区间内的边。此时,如果 u u u到 v v v连通就更新答案。
这个时间复杂度是 O ( q m 3 l o g n ) O(qm^3logn) O(qm3logn)的,原地爆炸。我们珂以考虑一个类似莫队的优化,我们先对所有边排序,询问时每次固定 l l l,右端点每次向右移动一位,每次 r r r加一的时候加上一条路径,只要连通了就直接更新答案并返回。这样时间复杂度为 O ( q m 2 l o g n ) O(qm^2logn) O(qm2logn)的,通常跑步满。
这样仍然会超时。怎么办呢?很简单,我们把并查集的合并改成启发式合并就做完了。
每走一步都是套路,而我太菜了,就是不会做……
HDU1811: 首先,我们按照并查集将 = = =连接的连通分量缩点。
现在,我们考虑如何处理。珂以发现, a > b a>b a>b与 a < b aa<b等价,我们只需要处理 < < <的情况。然后,套路地建图,接着拓扑排序;如果某一步珂以出队的有多个节点,就是"UNCERTAIN"(不确定);如果拓扑排序两次加入一个点或一个点也加不进来,就是"CONFLICT"(自相矛盾);否则就珂以找出相对的关系。
估计也只有这种大水题,我才能做出来吧QAQ
HDU3938: 我们离线,将所有询问排序。接着,我们每次加边,表示这些边能够经过;用一个并查集维护连通块,同时在合并两个连通块的同时统计不同路径的数量。
套路题,做出来了。
CF1093G: 这种套路么学过做不出来,还珂以安慰是自己笨。
QAQ
珂以发现, k k k特别小,我们珂以状压。
即,一个二进制位表示另一个坐标与它的关系。举个例子, 11 11 11就表示 01011 01011 01011,即 x 1 < y 1 , x 2 ≥ y 2 , x 3 < y 3 , x 4 ≥ y 4 , x 5 ≥ y 5 x_1
我们珂以考虑用线段树来维护一个区间中,二进制数 x x x所表示的情况的最大值。珂以发现, 0 0 0与 31 31 31, 7 7 7与 24 24 24等数相互对应,于是线段树的标记上传就很简单啦。这里有一个理解的难点: 万一这两个数对应的那个二进制不对怎么办?没事,这样只会让这个值变小,不会影响最大值。这个东西差点让我自闭,你们说说我是不是太菜了……
时间复杂度 O ( n l o g n 2 k ) O(nlogn2^k) O(nlogn2k)。
CF817F: 一个裸的动态开点权值线段树上二分求MEX的板子题。
这题很轻松就做出来,只是因为这个套路我学过。
首先,你先别管别的,开个大小为 4 ( r − l + 1 ) 4(r-l+1) 4(r−l+1)的权值线段树。MLE是不?就改成动态开点权值线段树。
看一下三个操作,可以发现是:
①区间取反
②区间摊为 1 1 1
③区间摊为 0 0 0
这三个操作可以用线段树直接搞定,没啥问题。但是 l a z y t a g lazytag lazytag的下穿顺序可能会影响答案,我们就把 l a z y t a g lazytag lazytag带上一个时间戳。
对于每次询问,我们直接动态开点权值线段树上二分就完了。
是不是很裸很水啊