IS-LM模型:从失衡到均衡的模拟
IS-LM模型:从失衡到均衡的模拟
文章目录
- IS-LM模型:从失衡到均衡的模拟
-
- @[toc]
- 1 I S − L M 1 IS-LM 1IS−LM模型
- 2 数值模拟
-
- 2.1 长期均衡解
- 2.2 政府部门引入
- 2.3 价格水平影响
- 2.4 随机扰动因素
文章目录
- IS-LM模型:从失衡到均衡的模拟
-
- @[toc]
- 1 I S − L M 1 IS-LM 1IS−LM模型
- 2 数值模拟
-
- 2.1 长期均衡解
- 2.2 政府部门引入
- 2.3 价格水平影响
- 2.4 随机扰动因素
1 I S − L M 1 IS-LM 1IS−LM模型
I S − L M IS-LM IS−LM是产品市场和货币市场共同均衡时的模型,它由两条曲线构成,分别是 I S IS IS曲线和 L M LM LM曲线。其中 I S IS IS曲线是在产品市场均衡(产品服务供给等于需求、计划支出等于实际支出、计划投资等于储蓄、非计划存货等于0)条件下,均衡实际收入 Y Y Y与实际利率 r r r之间的反向变化关系; L M LM LM曲线是在货币市场均衡(货币供给等于货币需求)条件下,均衡实际利率 r r r与实际收入 Y Y Y之间的正向变化关系。用方程表示为
{ Y = C ( Y ) + I ( r ) L ( r , Y ) = M / P \left\{\begin{array}{l} Y=C(Y)+I(r)\\ L(r,Y)=M/P \end{array}\right. {Y=C(Y)+I(r)L(r,Y)=M/P
其中 Y = C ( Y ) + I ( r ) Y=C(Y)+I(r) Y=C(Y)+I(r)为产品市场均衡条件(计划支出=实际支出)。消费 C ( Y ) C(Y) C(Y)是关于收入 Y Y Y的函数,假设是线性的:
C ( Y ) = α + β Y C(Y)=\alpha+\beta Y C(Y)=α+βY
其中 β ∈ ( 0 , 1 ) \beta\in(0,1) β∈(0,1)称为边际消费倾向, α > 0 \alpha>0 α>0为自主消费,即没有收入时的消费。在资本边际效率不变时,投资 I ( r ) I(r) I(r)是关于利率 r r r的递减函数,假设也是线性的:
I ( r ) = e − d r I(r)=e-dr I(r)=e−dr
其中 e > 0 e>0 e>0是自发投资, d d d是投资对利率的敏感程度。于是产品市场均衡条件可记作
Y = α + β Y + e − d r Y=\alpha+\beta Y+e-dr Y=α+βY+e−dr
L ( r , Y ) L(r,Y) L(r,Y)为实际货币需求,它是由 L 1 ( Y ) L_1(Y) L1(Y)需求和 L 2 ( r ) L_2(r) L2(r)需求构成。 L 1 ( Y ) L_1(Y) L1(Y)由交易性需求和预防性需求构成,随收入 Y Y Y增加而增加,不妨假定为正比例函数
L 1 ( Y ) = k Y L_1(Y)=kY L1(Y)=kY
其中 k k k表示用于支付日常开支(交易性需求)和未来不确定性(预防性需求)占实际收入的比重。 L 2 ( r ) L_2(r) L2(r)需求称为投机性需求,它是关于实际利率的递减函数,假设为负比例函数:
L 2 ( r ) = A − h r L_2(r)=A-hr L2(r)=A−hr
其中 A > 0 A>0 A>0是参数, h h h表示 L 2 L_2 L2对利率 r r r变化的敏感程度。 M M M表示名义货币供给, P P P表示价格水平, M / P M/P M/P表示实际货币供给。货币市场均衡条件可以记作
k Y + A − h r = M / P kY+A-hr=M/P kY+A−hr=M/P
我们将上述两个模型重新写在一起
{ Y = α + β Y + e − d r k Y + A − h r = M / P \left\{\begin{array}{l} Y=\alpha+\beta Y+e-dr\\ kY+A-hr=M/P \end{array}\right. {Y=α+βY+e−drkY+A−hr=M/P
将 r , Y r,Y r,Y视为内生变量,两个方程组可以解出唯一均衡值,记作 ( r ∗ , Y ∗ ) (r^*,Y^*) (r∗,Y∗)。其中 r ∗ r^* r∗称为均衡实际利率, Y ∗ Y^* Y∗称为均衡实际收入,或均衡国民收入。从几何上看,也就是这两条直线的交点。
然而,初始的实际收入和实际利率并不是均衡的,很有可能并不在上述两条直线的交点处,例如下图 E ′ E' E′, E ′ ′ E'' E′′和 E ′ ′ ′ E''' E′′′。
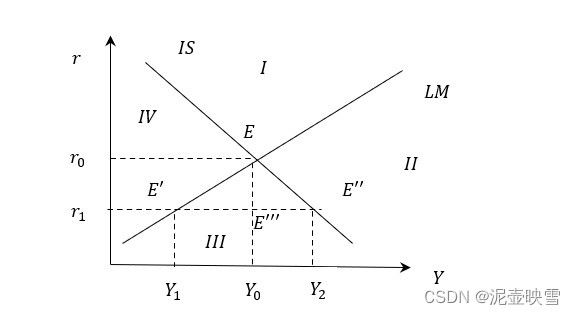
假设初始状态在 E ′ ′ ′ E''' E′′′,此时计划投资大于储蓄 I > S I>S I>S,实际收入 Y Y Y增加,实际利率 r r r增加,即 E ′ ′ ′ E''' E′′′点即向右移动,又向上移动,合力为右上方,直至进入 I I II II区域。在 I I II II区域中, I < S II<S,实际收入减少,于是向左移动; L > M L>M L>M,实际利率继续向上移动,合力为左上方,此时进入 I I I区域。在 I I I区域, Y Y Y减少, r r r降低,合力在左下方,进入 I V IV IV区域。在 I V IV IV区域, Y Y Y增加, r r r降低,进入 I I I III III区域,于是重新回到 I I I III III区域。但每次都与均衡点 E E E不断接近。
为了使上述模型动态化,引入时间因素 t t t,于是
{ C t = α + β Y t I t = e − d r t Y t + 1 = C t + I t k Y t + A − h r t + 1 = M / P \left\{\begin{array}{l} C_t = \alpha+\beta Y_t\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t\\ kY_t+A-hr_{t+1}=M/P \end{array}\right. ⎩ ⎨ ⎧Ct=α+βYtIt=e−drtYt+1=Ct+ItkYt+A−hrt+1=M/P
整理得到
{ C t = α + β Y t I t = e − d r t Y t + 1 = C t + I t r t + 1 = ( k Y t + A − M / P ) / h \left\{\begin{array}{l} C_t = \alpha+\beta Y_t\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t\\ r_{t+1} = (kY_t+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧Ct=α+βYtIt=e−drtYt+1=Ct+Itrt+1=(kYt+A−M/P)/h
在长期中,非均衡逐渐向均衡靠拢, r t ≈ r t + 1 ≈ r ∗ r_t\approx r_{t+1} \approx r^* rt≈rt+1≈r∗, Y t ≈ Y t + 1 ≈ Y ∗ Y_t\approx Y_{t+1}\approx Y^* Yt≈Yt+1≈Y∗,于是
{ C ∗ = α + β Y ∗ I ∗ = e − d r ∗ Y ∗ = C ∗ + I ∗ r ∗ = ( k Y ∗ + A − M / P ) / h \left\{\begin{array}{l} C^* = \alpha+\beta Y^*\\ I^*=e-dr^*\\ Y^*= C^*+I^*\\ r^* = (kY^*+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧C∗=α+βY∗I∗=e−dr∗Y∗=C∗+I∗r∗=(kY∗+A−M/P)/h
使用行列式求解得到长期均衡点为
{ r ∗ = k ( α + e ) + ( 1 − β ) ( A − M / P ) k d + h ( 1 − β ) Y ∗ = h ( α + e ) − d ( A − M / P ) k d + h ( 1 − β ) \left\{\begin{array}{l} r^* = \dfrac{k(\alpha+e)+(1-\beta)(A-M/P)}{kd+h(1-\beta)} \\ Y^* = \dfrac{h(\alpha+e)-d(A-M/P)}{kd+h(1-\beta)} \\ \end{array}\right. ⎩ ⎨ ⎧r∗=kd+h(1−β)k(α+e)+(1−β)(A−M/P)Y∗=kd+h(1−β)h(α+e)−d(A−M/P)
2 数值模拟
2.1 长期均衡解
令参数 α = 500 \alpha=500 α=500, β = 0.5 \beta=0.5 β=0.5, e = 1250 e=1250 e=1250, d = 250 d=250 d=250, k = 0.5 k=0.5 k=0.5, h = 250 h=250 h=250, A = 1000 A=1000 A=1000, M = 1250 M=1250 M=1250, P = 1 P=1 P=1,代入上述均衡解得到
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
r_star = (k*(alpha+e)+(1-beta)*(A-M/P))/(k*d+h*(1-beta))
Y_star =( h*(alpha+e)-d*(A-M/P))/(k*d+h*(1-beta))
r_star
Y_star
# 3
# 2000
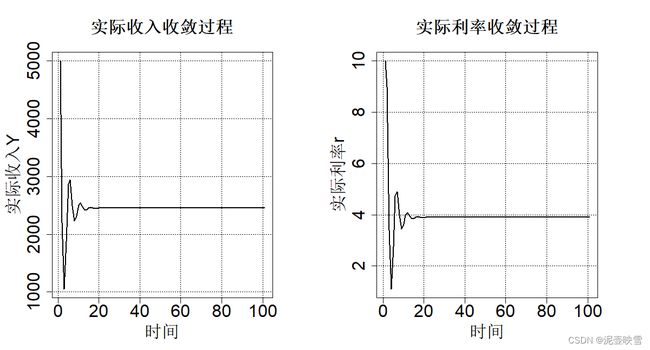
现在假设初始实际利率为 r 0 = 10 r_0=10 r0=10, Y 0 = 5000 Y_0=5000 Y0=5000,基于下列公式
{ C t = α + β Y t I t = e − d r t Y t + 1 = C t + I t r t + 1 = ( k Y t + A − M / P ) / h \left\{\begin{array}{l} C_t = \alpha+\beta Y_t\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t\\ r_{t+1} = (kY_t+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧Ct=α+βYtIt=e−drtYt+1=Ct+Itrt+1=(kYt+A−M/P)/h
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
T = 100 # 迭代次数
r = numeric()
Y = numeric()
# 初始值
r[1] = 10
Y[1] = 5000
# 迭代
for (t in 1:T) {
C = 500+0.5*Y[t]
I = 1250-250*r[t]
Y[t+1] = C+I
r[t+1] = (k*Y[t]+A-M/P)/h
}
par(mfrow=c(1,2),mar = c(5,5,5,5))
plot(Y,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际利率均衡过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
plot(r,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际收入均衡过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
par(mfrow=c(1,1))
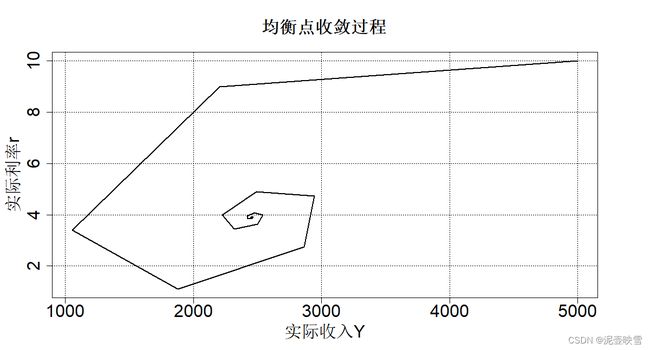
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "均衡点收敛过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
2.2 政府部门引入
引入政府部门,政府决策变量包括政府支出 G G G、税收 T T T和转移支付 T r T_r Tr,此时均衡条件如下:
{ C t = α + β ( Y t − T + T r ) I t = e − d r t Y t + 1 = C t + I t + G r t + 1 = ( k Y t + A − M / P ) / h \left\{\begin{array}{l} C_t = \alpha+\beta (Y_t-T+T_r)\\ I_t=e-dr_t\\ Y_{t+1}= C_t+I_t +G\\ r_{t+1} = (kY_t+A-M/P)/h \end{array}\right. ⎩ ⎨ ⎧Ct=α+β(Yt−T+Tr)It=e−drtYt+1=Ct+It+Grt+1=(kYt+A−M/P)/h
令政府购买 G = 500 G=500 G=500,税收 T = 20 T=20 T=20,转移支付 T r = 5 T_r=5 Tr=5,
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
T = 20
Tr = 5
G = 500
T = 100 # 迭代次数
r = numeric()
Y = numeric()
# 初始值
r[1] = 10
Y[1] = 5000
# 迭代
for (t in 1:T) {
C = 500+0.5*(Y[t]-T+Tr)
I = 1250-250*r[t]
Y[t+1] = C+I+G
r[t+1] = (k*Y[t]+A-M/P)/h
}
par(mfrow=c(1,2),mar = c(5,5,5,5))
plot(Y,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际利率均衡过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
plot(r,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际收入均衡过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
par(mfrow=c(1,1))
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "均衡点收敛过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
2.3 价格水平影响
使价格水平 P P P不断下降,实际货币供给不断增加,实际货币供给增加又导致均衡实际利率不断降低,进而导致投资不断增加,均衡国民收入不断增加。
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
T = 20
Tr = 5
G = 500
T = 100 # 迭代次数
r = numeric()
Y = numeric()
# 初始值
r[1] = 10
Y[1] = 5000
# 迭代
P = c(1,0.8,0.6,0.4)
par(mfrow=c(2,2),mar = c(5,5,5,5))
for(j in P){
for (t in 1:T) {
C = 500+0.5*(Y[t]-T+Tr)
I = 1250-250*r[t]
Y[t+1] = C+I+G
r[t+1] = (k*Y[t]+A-M/j)/h
}
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = paste("价格水平P=",j),
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
}
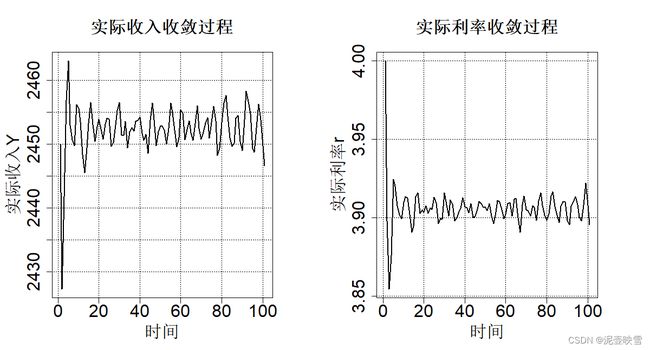
2.4 随机扰动因素
除收入外,还有其他一些因素也会影响消费;同理,除了利率,也有其他因素也会影响投资大小;货币需求和货币供给之间也存在随机误差。因此,均衡条件进一步改进为
{ C t = α + β ( Y t − T + T r ) + ε t I t = e − d r t + v t Y t + 1 = C t + I t + G r t + 1 = ( k Y t + A − M / P + w t ) / h ε t , v t , w t ∼ N ( 0 , 1 ) \left\{\begin{array}{l} C_t = \alpha+\beta (Y_t-T+T_r)+\varepsilon_t \\ I_t=e-dr_t+v_t\\ Y_{t+1}= C_t+I_t +G\\ r_{t+1} = (kY_t+A-M/P+w_t)/h\\ \varepsilon_t,v_t,w_t\sim N(0,1) \end{array}\right. ⎩ ⎨ ⎧Ct=α+β(Yt−T+Tr)+εtIt=e−drt+vtYt+1=Ct+It+Grt+1=(kYt+A−M/P+wt)/hεt,vt,wt∼N(0,1)
其中 ε t , v t , w t \varepsilon_t,v_t,w_t εt,vt,wt假定服从标准正态分布。
#------------------------随机扰动影响-----------------------------
rm(list = ls())
# 参数初始化
alpha = 500
beta = 0.5
e = 1250
d = 250
k = 0.5
h = 250
A = 1000
M = 1250
P = 1
T = 20
Tr = 5
G = 500
T = 100 # 迭代次数
r = numeric()
Y = numeric()
# 初始值
r[1] = 4
Y[1] = 2450
# 迭代
for (t in 1:T) {
C = 500+0.5*(Y[t]-T+Tr)+rnorm(1,0,1)
I = 1250-250*r[t]+rnorm(1,0,1)
Y[t+1] = C+I+G
r[t+1] = (k*Y[t]+A-M/P+rnorm(1,0,1) )/h
}
par(mfrow=c(1,2),mar = c(5,5,5,5))
plot(Y,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际利率均衡过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
plot(r,type = "l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "实际收入均衡过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")
par(mfrow=c(1,1))
plot(Y,r,typ="l",lwd=2,xlab = "实际收入Y",ylab = "实际利率r",main = "均衡点收敛过程",
cex.axis = 2, cex.lab = 2,cex.main = 2,family = "ST")
grid(col = "black")