代码随想录 Day40 动态规划08 LeetCodeT198打家劫舍 T213打家劫舍II T337 打家劫舍III

动规五部曲:

1.确定dp数组含义

2.确定递推公式

3.初始化dp数组

4.确定遍历顺序

5.打印数组排错

LeetCode T198 打家劫舍

题目链接:198. 打家劫舍 - 力扣（LeetCode）

题目思路:

今天我们走出背包问题,开始进入新一轮经典问题的学习:打家劫舍问题.

题目大概含义就是我们不能在相邻的两间房子偷东西,最后要求我们得到的最大钱数是多少,我们仍然使用动规五部曲来分析问题

1.确定dp数组含义

dp[i]偷到这一家获得的最大钱数(包含这一家,但是偷不偷不知道)所以我们可以理解为考虑而不是一定包含在内.

2.确定递推公式

就是取决于这一家偷或者不偷之间取得的最大值

dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1])

3.初始化dp数组

由于取值取决于前两家的价值,所以这里我们初始化前两个元素

dp[0] = nums[0];

dp[1] = Math.max(nums[0],nums[1]);

4.确定遍历顺序

从前向后遍历,因为后面的取决于前面元素的产生

5.打印数组排错

题目代码:

class Solution {
    public int rob(int[] nums) {
        if(nums.length == 1){
            return nums[0];
        }
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for(int i = 2;i

LeetCode T213 打家劫舍II

题目链接:213. 打家劫舍 II - 力扣（LeetCode）

题目思路:

这题其实就是在第一题的思路上加上了一个环,首尾相连,这样我们其实就是考虑两种情况即可,一个是包含头,那么就不能包含尾了,因为这里其实就是首尾是相邻的,所以就是将去头和去尾的数组重新进行第一题的打家劫舍操作,最后取最大值即可.

题目代码:

class Solution {
    public int rob(int[] nums) {
        if(nums.length == 1){
            return nums[0];
        }
        if(nums.length == 2){
            return Math.max(nums[0],nums[1]);
        }
        int[] tmp = new int[nums.length-1];
        int[] tmp1 = new int[nums.length-1];
        System.arraycopy(nums,0,tmp,0,nums.length-1);
        System.arraycopy(nums,1,tmp1,0,nums.length-1);
        return Math.max(rub1(tmp1),rub1(tmp));

    }
    public int rub1(int[] nums){
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for(int i = 2;i

LeetCode T337 打家劫舍III

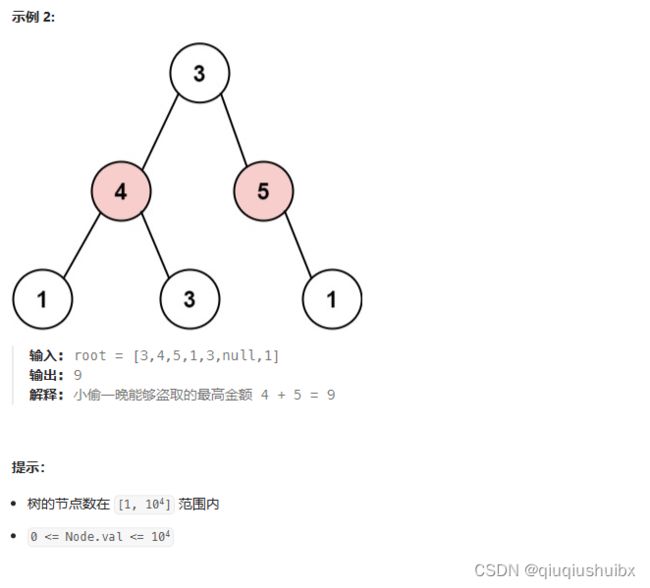
题目链接:337. 打家劫舍 III - 力扣（LeetCode）

题目思路:

树形dp的入门题,我们要使用二叉树那里的递归+动态规划来解决问题

1.确定递归参数和返回值

这里我们要求一个节点 偷与不偷的两个状态所得到的金钱，那么返回值就是一个长度为2的数组。我们规定dp[0]表示不偷,dp[1]表示偷

2.确定终止条件

当遇到空节点时,直接返回dp数组即可

3.确定遍历顺序

后序遍历,因为我们要获取左节点偷与不偷的情况和右节点偷与不偷的情况返回给父节点.

4.确定单层递归逻辑

此时就是父节点偷或者不偷

dp[0]就是不偷,就直接考虑左节点偷与不偷的最大值加上右节点偷与不偷的最大值.

dp[1]就是偷,就直接用该节点的值加上左节点不偷,右节点不偷的最大值

题目代码:

class Solution {
    public int rob(TreeNode root) {
        int[] res = robAction(root);
        return Math.max(res[0],res[1]);

    }
    public int[] robAction(TreeNode cur){
        int[] res = new int[2];
        if(cur == null){
            return res;
        }
        int[] dp_left = robAction(cur.left);
        int[] dp_right = robAction(cur.right);

        //不偷他就在左右都偷相加
        res[0] = Math.max(dp_left[0],dp_left[1])+Math.max(dp_right[0],dp_right[1]);
        res[1] = cur.val + dp_left[0] + dp_right[0];
        return res;
    }
}